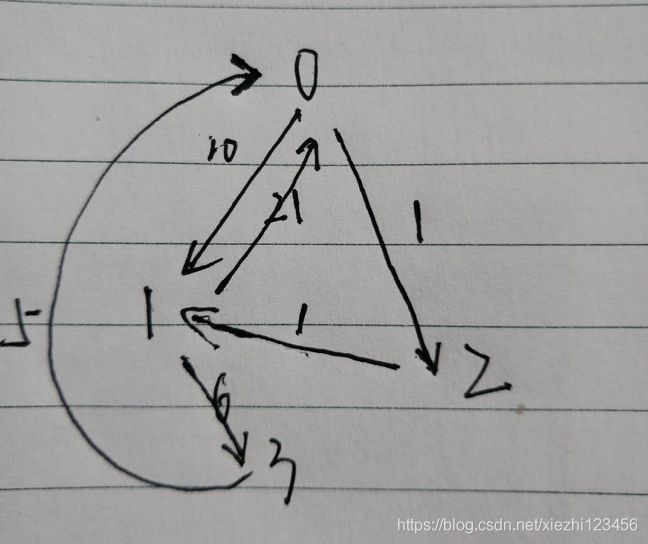
求带权有向图中的最小环

/**
*    实验题目:
*        求带权有向图中的最小环
*    实验目的:
*        掌握Floyd算法在求解实际问题中的应用。
*    实验内容:
*        编写一个程序，输出带权有向图中的一个最小环。
*    
*/

#include
#include

#define INF     32767               //定义∞
#define MAXV    100                 //最大顶点个数

typedef char InfoType;
/*-------------------------以下定义邻接矩阵类型---------------------------*/
typedef struct
{
    int no;                         //顶点编号
    InfoType info;                  //顶点信息
}VertexType;                        //顶点类型

typedef struct
{
    int edges[MAXV][MAXV];          //邻接矩阵数组(用一个二维数组存放顶点间关系(边或弧)的数据)
    int n;                          //顶点数
    int e;                          //边数
    VertexType vexs[MAXV];          //存放顶点信息(用一个一维数组存放图中所有顶点数据)
}MatGraph;                          //完整的图邻接矩阵类型

//邻接表表示法-将每个顶点的邻接点串成一个单链表
/*-----------以下定义邻接表类型--------------*/
typedef struct ArcNode
{
    int adjvex;                     //该边的邻接点编号
    struct ArcNode *nextarc;        //指向下一条边的指针
    int weight;                     //该边的相关信息,如权值(用整型表示)
}ArcNode;                           //边结点类型

typedef struct VNode
{
    InfoType info;                  //顶点其他信息
    int cnt;                        //存放顶点入度,仅用于拓扑排序
    ArcNode *firstarc;              //指向第一条边
}VNode;                             //邻接表结点类型

typedef struct
{
    VNode adjlist[MAXV];            //邻接表头结点数组
    int n;                          //图中顶点数
    int e;                          //图中边数
}AdjGraph;                          //完整的图邻接表类型

/*-------------------------邻接矩阵的基本运算算法---------------------------*/
/*------------由边数组A、顶点数n和边数e创建图的邻接矩阵g--------------------*/
void CreateMat(MatGraph &g, int A[MAXV][MAXV], int n, int e)
{
    int i, j;

    g.n = n;
    g.e = e;
    for(i = 0; i < g.n; i++)
        for(j = 0; j < g.n; j++)
            g.edges[i][j] = A[i][j];
}

/*------------输出邻接矩阵g--------------------*/
void DispMat(MatGraph g)
{
    int i, j;

    for(i = 0; i < g.n; i++)
    {
        for(j = 0; j < g.n; j++)
        {
            if(g.edges[i][j] != INF)
                printf("%4d", g.edges[i][j]);
            else
                printf("%4s", "∞");
        }
        printf("\n");
    }
}

/*-------------------------邻接表的基本运算算法---------------------------*/
/*-------------------由边数组A、顶点数n和边数e创建图的邻接表G--------------------*/
void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
    int i, j;
    ArcNode *p;

    G = (AdjGraph *)malloc(sizeof(AdjGraph));
    for(i = 0; i < n; i++)                              //给邻接表中所有头结点的指针域置初值NULL
    {
        G->adjlist[i].firstarc = NULL;
    }

    for(i = 0; i < n; i++)                              //检查邻接矩阵中的每个元素
    {
        for(j = n - 1; j >= 0; j--)
        {
            if(A[i][j] != 0 && A[i][j] != INF)          //存在一条边
            {
                p = (ArcNode *)malloc(sizeof(ArcNode)); //创建一个结点p
                p->adjvex = j;                          //邻接点编号
                p->weight = A[i][j];                    //边的权重
                p->nextarc = G->adjlist[i].firstarc;    //采用头插法插入结点p
                G->adjlist[i].firstarc = p;
            }
        }
    }
    G->n = n;
    G->e = e;
}

/*-------------------输出邻接表G--------------------*/
void DispAdj(AdjGraph *G)
{
    ArcNode *p;

    for(int i = 0; i < G->n; i++)
    {
        p = G->adjlist[i].firstarc;
        printf("顶点%d: ", i);
        while(p != NULL)
        {
            printf("%3d[%d]->", p->adjvex, p->weight);  //邻接点编号[权重]
            p = p->nextarc;
        }
        printf("∧\n");
    }
}

/*-------------------销毁图的邻接表G--------------------*/
void DestroyAdj(AdjGraph *&G)
{
    ArcNode *pre, *p;

    for(int i = 0; i < G->n; i++)
    {
        pre = G->adjlist[i].firstarc;                   //pre指向第i个单链表的首结点
        if(pre != NULL)
        {
            p = pre->nextarc;
            while(p != NULL)                            //释放第i个单链表的所有边结点
            {
                free(pre);
                pre = p;
                p = p->nextarc;
            }
            free(pre);
        }
    }
    free(G);                                            //释放头结点数组
}

/*--------------输出顶点i到j的一条最短路径---------------*/
static void Dispapath(int path[][MAXV], int i, int j)
{
    int apath[MAXV], d;
    int k = path[i][j];

    d = 0;                                      //路径上添加终点
    apath[d] = j;
    while((k != -1) && (k != i))                //路径上添加中间点
    {
        d++;
        apath[d] = k;
        k = path[i][k];
    }
    d++;
    apath[d] = i;                               //路径上添加起点
    for(int s = d; s >= 0; s--)                 //输出路径上的中间顶点
        printf("%d->", apath[s]);
}

/*--------------------在图g和A中查找一个最小环---------------------*/
static int Mincycle(MatGraph g, int A[MAXV][MAXV], int &min_i, int &min_j)
{
    int i, j, min_value = INF;

    for(i = 0; i < g.n; i++)
    {
        for(j = 0; j < g.n; j++)
        {
            if((i != j) && (g.edges[j][i] < INF))
            {
                if(A[i][j] + g.edges[j][i] < min_value)
                {
                    min_value = A[i][j] + g.edges[j][i];
                    min_i = i;
                    min_j = j;
                }
            }
        }
    }

    return min_value;
}

/*--------------Floyd算法求图中的一个最小环---------------*/
static void Floyd(MatGraph g)
{
    int A[MAXV][MAXV];
    int path[MAXV][MAXV];
    int i, j, k, min_value, min_i, min_j;

    for(i = 0; i < g.n; i++)
    {
        for(j = 0; j < g.n; j++)
        {
            A[i][j] = g.edges[i][j];
            if((i != j) && (g.edges[i][j] < INF))   //顶点i到j有边时
                path[i][j] = i;
            else                                    //顶点i到j没有边时
                path[i][j] = -1;
        }
    }

#if 0
    for(i = 0; i < g.n; i++)
    {
        for(j = 0; j < g.n; j++)
        {
            printf("%3d ", path[i][j]);
        }
        printf("\n");
    }
#endif

    for(k = 0; k < g.n; k++)                        //依次考察所有顶点
    {
        for(i = 0; i < g.n; i++)
        {
            for(j = 0; j < g.n; j++)
            {
                if(A[i][j] > A[i][k] + A[k][j])
                {
                    A[i][j] = A[i][k] + A[k][j];    //修改最短路径长度
                    path[i][j] = path[k][j];        //修改最短路径
                }
            }
        }
    }

    min_value = Mincycle(g, A, min_i, min_j);
    if(min_value != INF)
    {
        printf("  图中最小环: ");
        Dispapath(path, min_i, min_j);              //输出一条最短路径
        printf("%d, 长度: %d\n", min_i, min_value);
    }
    else
        printf("  图中没有任何环\n");

}

int main(void)
{
    MatGraph g;
    int A[MAXV][MAXV] = {
        {0, 10, 1, INF}, {21, 0, INF, 6},
        {INF, 1, 0, INF},{5, INF, INF, 0}
    };                                              //图的邻接矩阵:二维数组表示法
    int n = 4;                                      //图的顶点数
    int e = 6;                                      //图的边数

    CreateMat(g, A, n, e);                          //建立图的邻接矩阵
    printf("有向图G的邻接矩阵:\n");
    DispMat(g);
    printf("求解结果:\n");
    Floyd(g);

    return 0;
}

测试结果:

有向图G的邻接矩阵:
   0  10   1  ∞
  21   0  ∞   6
  ∞   1   0  ∞
   5  ∞  ∞   0
求解结果:
  图中最小环: 0->2->1->3->0, 长度: 13