multi-teacher学习

多老师学习：
1.Learning from Multiple Teacher Networks
1)不同example 输入到网络会有不同的输出，（x1,x2,x3）得到（p1,p2,p3）,(q1,q2,q3)，怎么保证||q1-q2||和||q1-q3||的相对距离（q2和q3谁取胜）和||p1-p2||和||p1-p3||的相对距离相近（p2和p3谁取胜）。
2)如果是多个老师的话，因为不同老师可能结果不同还是有噪音，所以取老师们中数量较多的结果。作为multi-teachers的结果。
3)具体还有选择哪些层作为immediate layer。
问题：训练实例输出的距离差感觉不适合NLP。

2.MOG,
1）是chair通过隐向量来动态决定权重的。
2）共用一个encoder的（teach的模型，针对不同的数据源，应该encoder参数也不同？应该retrieval一个不用考虑这个问题）
3）experts是分领域训练的，chair是整个数据集训练的（感觉可以删掉，毕竟是要一个简单的stud模型）。
问题：expert需要预训练。没看懂chair怎么整合的。
4）
experts怎么融合。
${\mathbf{p}}_j={\sum }_{l=1}^{k+1}{\beta }_j^l\cdot {\mathbf{p}}_j^l$
$\begin{array}{rl}{\beta }_j^l& =\frac{\exp \left(u_l^T{u}_{e,l}\right)}{{\sum }_{b=1}^k\exp \left(u_b^T{u}_{e,l}\right)}\\ u_l& =\mathrm{MLP}(\mathbf{h})\\ \mathbf{h}& ={\mathbf{s}}_j^1\oplus {\mathbf{p}}_j^1\oplus \cdots \oplus {\mathbf{s}}_j^k\oplus {\mathbf{p}}_j^k\oplus {\mathbf{s}}_j^{k+1}\oplus {\mathbf{p}}_j^{k+1}\end{array}$
$u_{e,l}$ is an expert-specific, learnable vector that reflects which dimension of the projected hidden representation is highlighted for the expert. 在第j步时$u_l^T$是所有状态加起来。
loss怎么计算
1)experts的loss
${\mathcal{L}}_{\text{experts}}={\sum }_{l=1}^{k+1}{\sum }_{\left(X^l,Y^l\right)\in S_l}{\sum }_{j=1}^n{\mu }_k{y}_j^l\log {\mathbf{p}}_j^l$
2)chair的loss
${\mathcal{L}}_{\text{chair}}={\sum }_{r=1}^{\lfloor D\rfloor }{\sum }_{j=1}^n{y}_j\log {\mathbf{p}}_j$
3)模型在训练时候的loss
$\mathcal{L}=\lambda \cdot {\mathcal{L}}_{\text{experts}}+(1-\lambda )\cdot {\mathcal{L}}_{\text{chair}}$

→关于$U_{e,l}$的公式怎么来的，
2.2 Granger-causal Attentive Mixtures of Experts: Learning Important Features with Neural Networks
$h_{\mathrm{a}\mathrm{l}\mathrm{l}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{e}\left(h_1,c_1,h_2,c_2,\dots ,h_p,c_p\right)$

$y={\sum }_{i=1}^p\underset{a_i}{G_i\left(h_{\text{all }}\right)}\underset{c_i}{E_i\left(x_i\right)}$

$a_i=\frac{\exp \left(u_i^T{u}_{s,i}\right)}{{\sum }_{j=1}^p\exp \left(u_j^T{u}_{s,i}\right)}$
$u_i=\mathrm{activation}\left(W_i{h}_{\mathrm{a}\mathrm{l}\mathrm{l}}+b_i\right)$

说的是$u_{s,i}$是需要学习的vector，值得是针对当前teach需要提取出什么特征。对于$u_i^T$指的是对于全部teachs的输出，代表了所有信息，通过Wb提取出当前teach对应的信息。目前理解是这样，还需要对照代码。
代码地址：https://github.com/d909b/ame

3.all_rounder for 语音
背景介绍：
1）单teacher训练
stud训练的目标是降低和老师输出结果之间的KL散度。
$L_{KLD}(\theta )=-{\sum }_l{p}_t(l|x)\log p_s(l|x)$
2）多teacher训练
只是将多老师的输出加权起来，仍然作为soft label。
$p_t(l|x)={\sum }_{k=1}^N{w}_k{p}_{tk}(l|x)$
3）我们的模型：
$p_t(l|x)=\left(1-w_{hard}\right)p_t^d(l|x)+w_{hard}{\delta }_t(l)$
teacher是在全数据集上经过了预训练，然后特定领域finetune。
stud训练（没有预训练）的时候，只考虑和他一样domain的老师的输出作为soft label，再加上本身的真值。

4.Distilled Person Re-identification: Towards a More Scalable System
这篇论文重点：adaptive knowledge aggregation
1）teacher知识：
${\mathbf{X}}_S=\left[{\mathbf{x}}_{S,1},{\mathbf{x}}_{S,2},\dots ,{\mathbf{x}}_{S,N}\right]\in {\mathbb{R}}^{d\times N}$是${\left\{{\mathbf{I}}_i\right\}}_{i=1}^N$的feature map, 学生网络的相似度矩阵$\mathbf{A}\mathbf{s}$（samples之间的相似度矩阵，对于re-ID来说就是判断对象),
${\mathbf{A}}_S={\mathbf{X}}_S^{\top }{\mathbf{X}}_S$
$\text{ where }{a}_{S,i,j}={\mathbf{x}}_{S,i}^{\top }{\mathbf{x}}_{S,j}\text{ in }{\mathbf{A}}_S\text{ is the cosine similarity be}\text{ tween samples }{\mathbf{I}}_i\text{ and }{\mathbf{I}}_j$
2）teacher传给stud：
$\min \mathrm{dist}\left({\mathbf{A}}_S,{\mathbf{A}}_T\right)$
dist计算$\mathrm{dist}\left({\mathbf{A}}_S,{\mathbf{A}}_T\right)={\Vert \log \left({\mathbf{A}}_S\right)-\log \left({\mathbf{A}}_T\right)\Vert }_F$
$\log (\mathbf{A})=\mathbf{U}\mathrm{diag}\left(\log \left({\lambda }_1\right),\log \left({\lambda }_2\right),\dots ,\log \left({\lambda }_N\right)\right){\mathbf{U}}^{\top }$
3）多个老师，也是权重不同老师输出，然后优化$\min dist$。
${\min }_{{\Theta }_S}{L}_T\left({\mathbf{X}}_S\right)={\Vert \log \left({\mathbf{X}}_S^{\top }{\mathbf{X}}_S\right)-\log \left({\mathbf{A}}_T\right)\Vert }_F^2$
4)权重判断
Du和DL里面没有相同的identity，【DL里面identity相同的两张图（a，b）的距离】要比【(a,随便从Du抽一张图)的距离】要大。
$L_{VER}\left({\mathbf{X}}_S^U,{\mathbf{X}}_S^L\right)={\sum }_{(i,j)\in {\mathcal{P}}_L}-\log \frac{\exp \left({\mathbf{x}}_{S,i}^{LT}{\mathbf{x}}_{S,j}^L\right)}{\exp \left({\mathbf{x}}_{S,i}^{L\top }{\mathbf{x}}_{S,j}^L\right)+{\sum }_{k=1}^N\exp \left({\mathbf{x}}_{S,i}^{L\top }{\mathbf{x}}_{S,k}^U\right)}$
因为没有真值，找了一个分布一致性作为真值。通过样本类别不同，来近似的圈出不同teacher的贡献度。
Adaptive Knowledge Aggregator. 对于超参数的确定，本来stud直接跟着老师的步伐走，是通过验证集标签集合的粗分类情况来调整超参数。
过程：老师结果作为真值（因为没有真值）来更新学生参数，验证集上结果来更新超参数。论文里说的却是倒过来的。

5.Amalgamating Knowledge towards Comprehensive Classification
过程：
1）feature amalgamation：input到teachers网络，得到的feature map拼接起来作为stud的feature map。
2）parameter learning：layer1->layer2，知道输入输出，训练网络参数。但是输入输出都是double-size，通过自编码器实现降维。
总结：
1）teachers的所有输出都是直接concat，包括最后的softmax 分类结果。
2）loss包括teachers的自编码误差，和每层学生输出和老师输出之间误差，和最后结果之间的误差。

6.Ensemble Knowledge Distillation for Learning Improved and Efficient Networks
这篇文章感觉质量不是很高。没有投到任何顶会。写作还是比较流畅的（我能学到一些表达）

总体思路：
stud有Ns个分支，每个分支的模型都是3层dense layer(中间加的有pooling等操作)。
而teacher网络是选的主流网络，（ we considered up to 7 sub-networks based on ResNet14, ResNet20, ResNet26, ResNet32, ResNet44, ResNet56, and ResNet110 architectures）.
loss是stud每个分支和每个teach对应的输出KL散度。还有teach在当前数据集的失败率（with真值）。还有stud自己在当前数据集的失败率（with真值）。
这个模型不够简洁。也很意外的出现了训练老师的情况。我不打算训练老师了。

7, 对于esim的深入理解
感觉论文并没有很深入的探讨。
基本公式我也记得差不多了，
参数，第一层lstm，第二层的mlp，第三层的lstm和mlp，

8.老师新给的文章：
progressive teacher-student learning

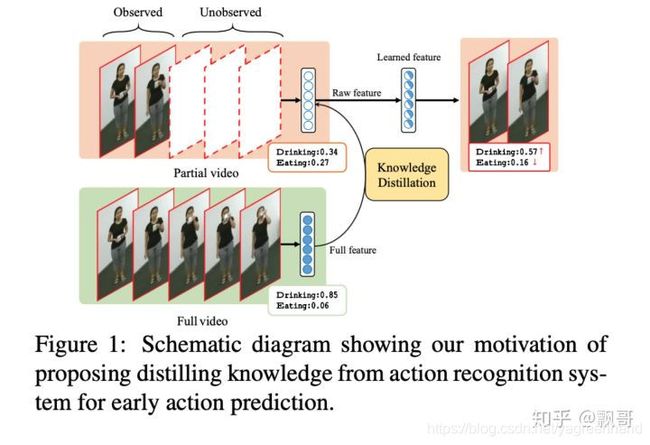
希望通过完整视频的学习提升部分视频的学习，在行为预测中需要对部分视频的行为进行分析和识别。
本文实验证明了完整视频的动作信息是可以用来蒸馏来提升行为预测的。

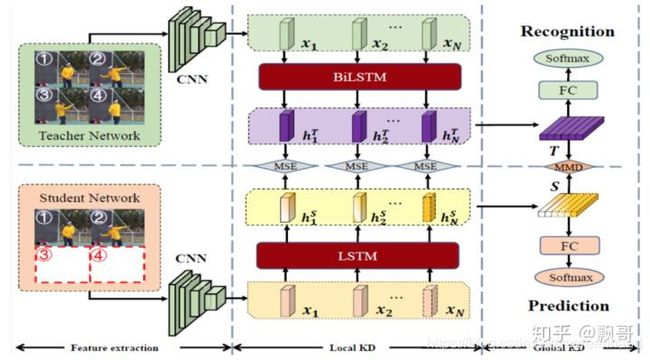
teacher网络用双向的lstm建模，student网络用单向的lstm建模，这么设计的原因是可以正向和反向推导完整的视频，但是不完整的视频未来的信息我们是不清楚的，所以只能单向的去预测。
本文设计的teacher-student learning是两个不同任务的一个信息蒸馏。Teacher是行为识别的任务，student是行为预测的任务，这是一个跨任务的信息蒸馏。


总的loss:
$L=\frac{1}{I}{\sum }_{i=1}^I\left(L_C\left({\mathbf{S}}_i,{\mathbf{y}}_i\right)+L_{TS}\left({\mathbf{S}}_i,{\mathbf{T}}_i\right)\right)$
stud和teach中间层的知识传递：
ere, $Si$ and $Ti$ are two $D\times N$-sized matrices. $D$是feature 维度， $N$ is lstm的层数(the total number of progress levels used for early action prediction)，
是直接每层的$h_i$取一个加权平均，因为每个阶段的输出贡献可能不同。
最终层的loss想直接抄过来。