快速傅里叶变换(FFT)

快速傅里叶变换(FFT)

---

例题:UOJ#34. 多项式乘法

题目描述
给你两个多项式，请输出乘起来后的多项式。
输入格式
第一行两个整数 n 和 m，分别表示两个多项式的次数。
第二行 n+1 个整数，分别表示第一个多项式的 0 到 n 次项前的系数。
第三行 m+1 个整数，分别表示第一个多项式的 0 到 m 次项前的系数。
输出格式
一行 n+m+1 个整数，分别表示乘起来后的多项式的 0 到 n+m 次项前的系数。
样例
input:
1 2
1 2
1 2 1
output:
1 4 5 2
explanation:
(1+2x)⋅(1+2x+x2)=1+4x+5x2+2x3
限制与约定
0≤n , m≤ 105

简要解析

首先这道涉及多项式乘法,求相乘后新多项式的系数,可简记为:

C(x)=A(x)∗B(x)=∑j=02∗n−2(∑k=0jak∗bk−j)xj

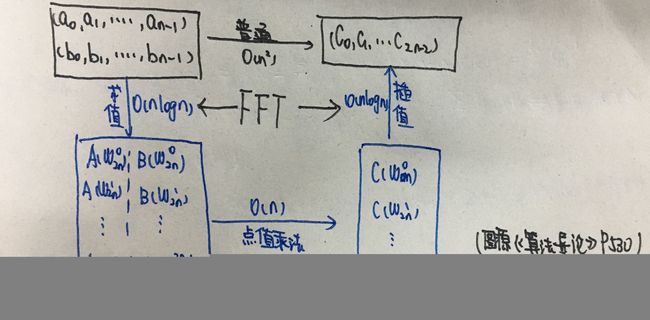
正常算法的时间复杂度很容易得到,即O( n2 ),显然无法再规定时间内得到正确解,怎么办呢?这里我们介绍一种可在O( nlgn )复杂度下快速求出该答案的方法,即FFT.希望读者在阅读此文后可自行编写!

多项式

多项式的表示

• 系数表达
  系数表达是我们平时最常见的表示多项式的方法,对任意一个多项式 A(x)=∑n−1i=0aixi ,其系数表示为

  A(x)=(a0,a1,…,an−1)
  
  系数表达的优势是它很容易求出该多项式在点 x0 处的值 A(x0) ,即利用霍纳法则(也称秦九韶算法):
  A(x0)=a0+x0(a1+x0(a2+⋯+x0(an−2+x0an−1)…))

• 点值表达
  所谓点值表达就是将一个次数界为n的多项式用 n个点值对 的集合来表示,即:
  

  A(x)={(x0,y0),(x1,y1),(x2,y2)…(xn−1,yn−1)}
  
  需要注意的是,一定需要n个点值对来表示,因为只有点值对数等于多项式的次数界时,其插值(由点值表达确定该多项式的系数表达,后边会讲到)才明确,这个结论可以由插值多项式的唯一性证明:
  
  ∣∣∣∣∣∣∣∣11⋮1x0x1⋮xn−1x20x21⋮x2n−1⋯⋯⋯xn−10xn−11⋮xn−1n−1∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣a0a1a2⋮an−1∣∣∣∣∣∣∣∣∣=∣∣∣∣∣∣∣∣∣∣y0y1y2⋮yn−1∣∣∣∣∣∣∣∣∣∣
  
  先将多项式转化为矩阵乘法的形式,其中第一项为范德蒙德行列式,记为 V(x0,x1,x2,…,xn−1) ,其值为 ∏0≤j<k≤n−1(xk−xj) ,显然当任意两个x值不同时该值不为0,故该矩阵可逆,进而可以求得 a=V(x0,x1,x2,…,xn−1)−1y , 故其唯一性得证!

  点值表示有什么优势呢?我们可以在O(n)的时间内求出两多项式的乘积!如果我们有一种很快的算法可以将系数表达式转化为点值表达式,那么我们就可以快速计算出两多项式的乘积.为了快速实现两种表达方式的快速转化,我们引入一个概念,* 单 位 复 数 根 *!

单位复数根

定义

满足 wn=1 的复数 w ,其单位复数根恰好有n个,分别为 e2πik/n,k={0,1,2,…,n−1} ,由复数的指数形式定义 eiu=cos(u)+isin(u) 可将其转化为 yk=cos(2πk/n)+isin(2πk/n)

基本性质

• 消去引理
  
  Wdkdn=(e2πi/dn)kn=(e2πi/d)k=Wkn(n≥0,k≥0,d>0)
• 折半引理
  若n>0且为偶数,那么n个n次单位复数根的平方的集合就是 n/2 个 n/2 次单位复数根的集合(每个元素出现两次)
  (Wk+n/2n)2=W2k+nn=W2kn⋅Wnn=(Wkn)2=Wkn/2
• 求和引理
  
  ∑j=0n−1(Wkn)j=(Wkn)n−1Wkn−1=(Wnn)k−1Wkn−1=0

DFT离散傅里叶变换

这个算法的核心是利用了卷积定理

a×b=DFT−12n(DFT2n(a)⋅DFT2n(b))

本文最开始的例题UOJ#34,目标多项式的系数 ck=∑jk=0ak∗bk−j ,熟悉的人可能都知道这实际上就是a,b的卷积,能用傅里叶变换求解的题目一般都可以被转化成类似这样的卷积的形式,大家一定要对这个式子足够熟悉!!!

yk=A(Wkn)=∑j=0n−1aj⋅Wkjn=∑j=0n−1aj⋅e2πinjk

该算法的复杂度是O( n2 )的,有没有适当变换使其结合一些复数根的性质加速此过程?答案是肯定的!

FFT快速傅里叶变换

递归

利用分治的思想将 A(x)=a0+a1x+a2x2+⋯+an−1xn−1 分为下标为奇数和偶数的两部分:

A[0](x)=a0+a2x+a4x2+⋯+an−2xn2−1

A[1](x)=a1+a3x+a5x2+⋯+an−1xn2−1

A(x)=A[0](x2)+x∗A[1](x2)

这样的话问题就可以转化求在 (W0n)2,(W1n)2,…,(Wn−1n)2 上A(x)值,又根据折半引理,只需计算次数界为n/2的值即可,这样一直递归下去,即可在O( nlgn )复杂度内计算出结果,附上伪代码:

FFT(a):  
    n=a.length()  
    if n==1:  
        return a  
    w_n=e^(pi*i/n)=complex(cos(2*pi/n),sin(2*pi/n))  
    w=1  
    a(0)=[a0,a2,...a_n-2]  
    a(1)=[a1,a3,...a_n-1]  
    y(0)=FFT(a(0))  
    y(1)=FFT(a(1))  
    for k in range(0,n/2):  
        y_k=y_k(0)+w*y_k(1)                     //w*y_k(1)为公用子表达式 
        y_k+n/2=y_k(0)-w*y_k(1)  
        w=w*w_n                                 //w为旋转因子
    return y  

但递归的常数是很大的,我们是否可以进一步优化常数呢?只要将递归过程改为迭代的过程就好了!

迭代

• 位逆序置换
  
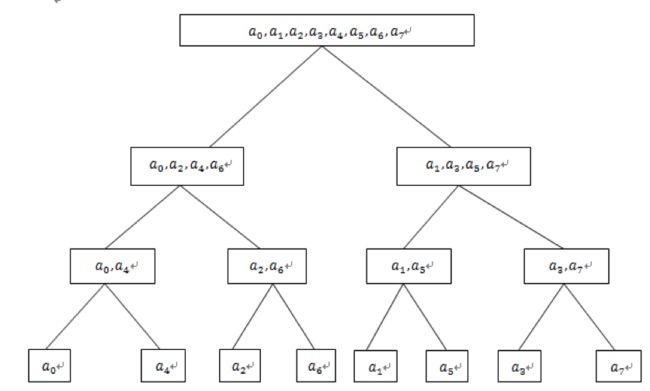
  观察其下标序列为
  0,4,2,6,1,5,3,7
  
  对应的二进制数为
  000,100,010,110,001,101,011,111
  
  若将每个数的二进制位反转,即得到
  000,001,010,011,100,101,110,111
  
  显然为0~7这8个数的升序排列,这样我们就找到了运算顺序与下标间的对应关系,这个过程就叫做位逆序置换,这样我们只要在计算之前将下标通过位逆序置换的方式更新即可按序自底向上求解,代码很简单:

inline int rev(int x,int n)                 //x为当前处理的待改变的数,n为二进制位的总长度(按上例则n=3)
{
    int x0=0;
    while(n--) x0=(x0+(x&1))<<1,x>>=1;
    return x0>>1;
}

• 蝴蝶操作
  
  yk=A(Wkn)=y[0]k+Wkn⋅y[1]k
  
  
  yk+n2=A(Wk+n2n)=A[0](W2k+nn)+Wk+n2n⋅A[1](W2k+nn)=A[0](W2kn)+Wk+n2n⋅A[1](W2kn)=y[0]k−Wkn⋅y[1]k

因此只要知道出 y[0]k 与 Wkn⋅y[1]k 的值就可直接算出 yk 与 yk+n2 的值,只要将上一步中分成的树状结构从下向上计算一遍就能求出答案了,这一操作也被称为蝴 蝶 操 作,伪代码如下:

for k in range(0,n/2):  
    t=w*y_k(1)  
    y_k=y_k(0)+t  
    y_k+n/2=y_k(0)-t  
    w=w*w_n 

傅里叶逆变换公式

以上我们了解到如何将系数表示转换为点值表示,通过点值表示在O(n)复杂度下求出多项式的乘积之后只要再将点值表示转换为系数表示(求插值)即可.前面讲多项式的点值表达时我们提到了一种求插值的过程, a=V(x0,x1,x2,…,xn−1)−1⋅y , 即只要得到范德蒙德行列式的逆矩阵就能求出对应的a.

由于一个矩阵的逆矩阵 A−1=1|A|A∗ ,易推得傅里叶逆变换公式:

ak=1n∑j=0n−1yj⋅e−2πinjk

除了这种求逆矩阵的方法,我们还可以用拉格朗日公式求插值,但复杂度为O( n2 ),公式如下:

A(x)=∑k=0n−1yk∏j≠k(x−xj)∏j≠k(xj−xk)

完整代码

大家最想要的代码来了,UOJ#34 AC代码:

#include
#define pi acos(-1.0)
#define maxn 300010
//#define DEBUG                                     //DEBUG无视就好
using namespace std;
int n,m;
complex<double> a[maxn],b[maxn];

inline int read()                                   //读入优化
{
    char ch;
    int read=0;
    int sign=1;
    do
        ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-');
    if(ch=='-') sign=-1,ch=getchar();
    while(ch>='0'&&ch<='9')
    {
        read=read*10+ch-'0';
        ch=getchar(); 
    } 
    return read*sign;
}

int Power2(int x)                                 //把x转化为2的整数次幂
{
    int x0;
    for(x0=1;x0<=x;x0<<=1) ;
    return x0;
}

inline int lg(int n)                             //计算二进制位数
{
    int l=0;
    if(n==0) return l;
    for(int x=1;x<=n;x<<=1) l++;
    return l;
}

inline int rev(int x,int n)                      //位逆序置换
{
    int x0=0;
    while(n--) x0=(x0+(x&1))<<1,x>>=1;
    return x0>>1;
}

void FFT(complex<double> a[],int n,int flag)    //主体
{
    complex<double> A[n+1];
    for(int i=0,l=lg(n-1);i#ifdef DEBUG
        int l=lg(n-1);                          //切记是lg(n-1)
    cerr<<"l="<for(int i=0;icerr<" ";
    cerr<#endif 
        for(int i=2;i<=n;i<<=1)                 //枚举合并后序列长度
    {
        complex<double> dw(cos(2*pi/i),sin(flag*2*pi/i));
        for(int j=0;j//该长度下每部分进行求解
        {
            complex<double> w(1.0,0);
            for(int k=0;k<(i>>1);k++,w=w*dw)    //蝴蝶变换,只需求i>>1次 
            {
                complex<double> u=A[j+k];
                complex<double> t=w*A[j+k+(i>>1)];
                A[j+k]=u+t;
                A[j+k+(i>>1)]=u-t;
            }
        }
        if(flag==-1)
            for(int i=0;iint(A[i].real()/n+0.5);
        else
            for(int i=0;iint main()
{
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    n=read();
    m=read();
    for(int i=0;i<=n;++i) a[i]=read();
    for(int i=0;i<=m;++i) b[i]=read();
    int length=Power2(n+m);
    #ifdef DEBUG
    cerr<<"length="<#endif
    FFT(a,length,1);
    FFT(b,length,1);
    for(int i=0;i<=length;++i) a[i]*=b[i];
    FFT(a,length,-1);
    for(int i=0;i<=n+m;++i) printf("%d ",int(a[i].real()));
    return 0;
}

参考资料

http://blog.csdn.net/oiljt12138/article/details/54810204
http://blog.csdn.net/iamzky/article/details/22712347
算法导论第三十章

如有疑问欢迎积极评论 !