系统框图

问题提出卓大大，这些圈，矩形，加减是什么意思？

^直立车模控制算法框图 | 公众号留图^

这位同学的提问时针对在几年前智能车竞赛组委会公布的一份直立车模控制参考设计方案文档中的算法描述框图。对于已经前期学习过“自动控制原理”，“信号与系统”课程的同学来讲，文档中描述算法的系统框图是简单的，但对于初学者来讲，看懂系统框图还需要了解 一些基本概念。

^四轮车模直立运行 | 公众号留图^

假设你已经对于“信号”、“系统”、信号的描述和运算、系统的分类以及

线性时不变系统有了基本的概念

，下面介绍描述系统（算法）的基本方法。基本原理****None描述线性时不变系统（动态）的常用方法有数学方程法、系统框图方法等。

（1）数学方程法数学方程方法就是把线性是不变系统的输入输出信号之间的关系，通过一个微分方程或者差分方程表达出来。这种方法比较简洁、便于求解，但无法描述系统内部信号之间的运算关系。

^{系统模块及其输入、输出信号，包括连续和离散时间信号}

基本的方式如下图所示：

^{描述连续和离散时间系统的常系数微分方程和差分方程}

方程表达了系统输入输出信号之间的隐含关系。通过求解微分（差分）方程可以将输出信号通过输入信号的显示数学表达式表示出来。

现代控制理论和信号处理还常常采用矩阵形式来描述系统内部状态变量下的多元微分方程租，提高了描述系统的精度。

（2）系统框图.

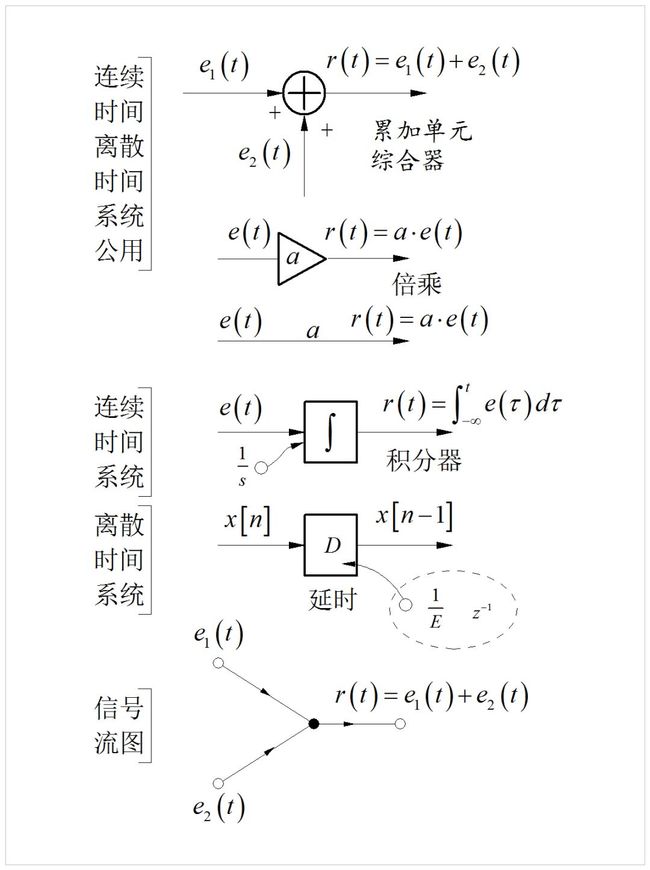
系统框图定义了一些描述信号基本运算的基本单元，通常包括加、乘、积分、微分、延迟、卷积和相关等等。

^{常用到的系统框图基本元素}

为了简化，将信号的倍乘通常表示在信号通道直线旁的一个数字（标量），比如上面表示信号倍乘a倍的情

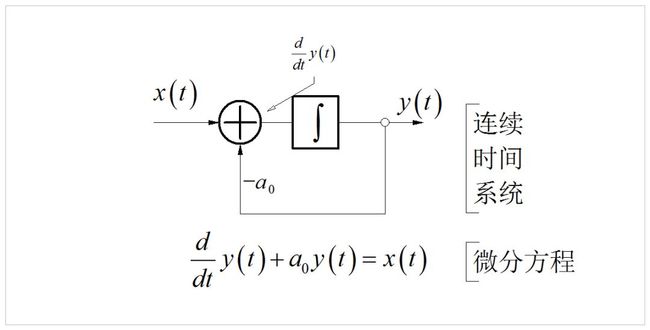
况。这些基本单元在通过串联、并联和反馈等组成更加复杂的系统框图，来描述实际系统（算法）的内部结构。比如下面就是一个最基本的反馈系统，与其对应的微分方程就在系统下面。

^{一个简单的反馈系统及其对应的微分方程}

系统框图不仅比较形象揭示出复杂系统内部的结构，而且为系统的物理实现提供了帮助。通常借助于一定的方法（信号流图）还可以对系统进行简化和变形。

对于一个确定的系统框图，可以得到与其对应的唯一数学方程。但对于数学方程描述的系统，则可以绘制出多种可以实现的等效的系统框图。

^{带有两个综合器的系统}

问题分析基于以上介绍，大家不仅可以对于常见到的动态系统使用系统框图对齐进行描述，在此基础上，还可以进一步完成系统的仿真、分析和实现。

1）MATLAB与系统仿真MATLAB是一种被广泛使用的算法开发、数据可视化、分析、计算的高级交互式语言开发环境。主要包括有MATLAB和Simulink两部分。Simulink众多的仿真工具箱为系统的搭建和仿真提供了很大的便利。

^{MATLAB中的SIMULINK工具进行两轮运动车模控制}

相比于前给出的几个教科书上的基本系统框图元素，在MATLAB中Simulink Library提供了众多的建立系统框图的模块。这些部件涵盖了众多的应用领域以及各式各样实际系统中存在的特殊部件。这位快速建立众多和实际系统相符的系统框图提供了很大的便利。

^{Simulink中众多的系统框图组件}

在系统框中添加适当的信号激励和观察模块，运行系统仿真可以获得系统的信号输出。有了这样的工具，可以在不需要了解任何自动控制数学分析原理的基础上完成系统特性的分析。

2）数学分析与代码实现虽然系统仿真软件简化了对于系统框图仿真分析过程，但对于典型简单的系统框图进行数学描述分析，一方面可以获得系统的传递函数，进而分析系统的时域和频域特性。另一方面可以将系统框图转换成对应的数学描述方程从而进一步完成软件算法实现。此时，系统框图也可以看成控制算法框图。

^{电磁直立车模控制算法框图}

俗话说，熟能生巧。如果对于系统框图理解比较透彻，同时具备了软件编写的经验，实际上也可以直接对照系统框图编写对应的软件代码。下面这张图就是在“电磁直立车模调试指南”中给出的系统框图与代码实现的对应实现。

^{系统框图与对应的算法代码}

3）系统实现代码如果说上面直接根据算法框图完成代码编写还需要经验的积累和软件调试的功底，那么直接使用一个按钮就可以将系统框图算法变成可以编译成一些嵌入式MCU中执行程序则就将工程师彻底解放出来了。

MATLAB中提供了系统控制框图直接生成C代码的功能，使用它可以大大加快嵌入式控制系统的开发。

^{SIMULINK直接生成嵌入式C代码程序}

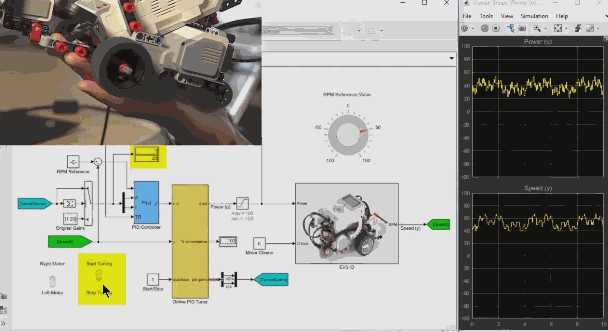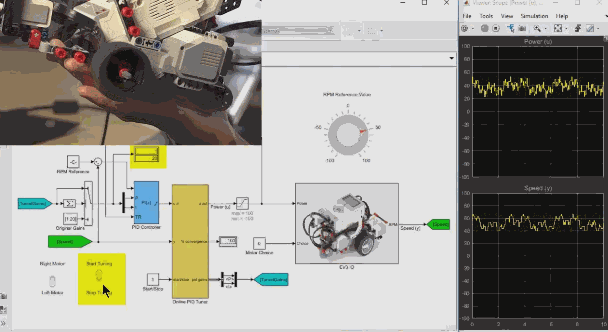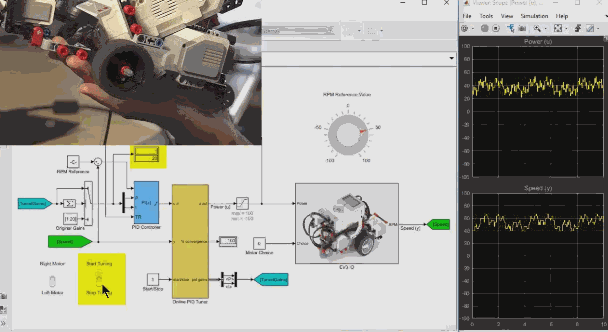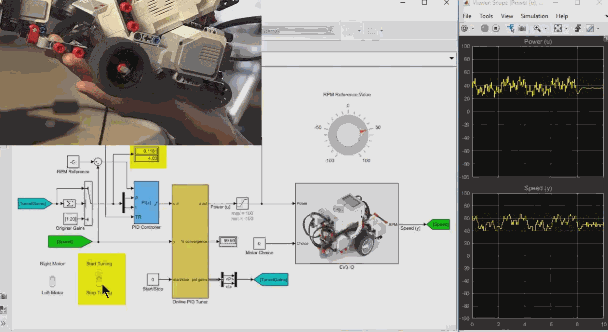
实验验证1） MATLAB系统仿真在MATLAB中的SIMULINK使用其中基本的 元器件搭建出本文最开始图中所示的直立车中互补滤波算法。

在系统框图的左下角通过MATLAB中的变量给定了实际角度数值。通过一个微分算子产生角加速度数值，模拟实际系统中IMU给出的陀螺仪信号。为了模拟实际中加速度传感器中由于车模运动所带来的噪声，在实际角度数值中叠加了一个白噪声。

^{Simulink搭建的互补滤波器算法框图}

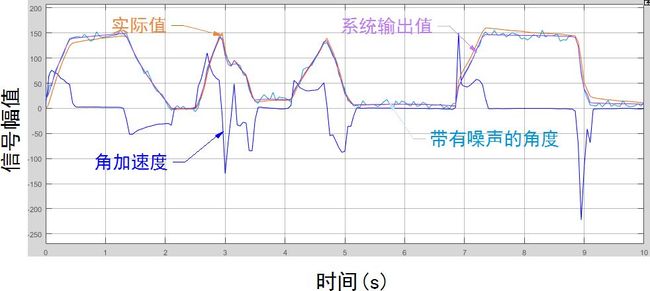
系统运行后得到的示波器显示的结果如下图所示：

算法输出的结果与实际值非常接近。通过改变算法中加速度反馈时间常数可以观察到抑制噪声方面的性能。

2）MATLAB中PID算法C语言代码生成PID是进行反馈控制的基本算法，在MATLAB中给出的离散PID控制器采用了并行PID的形式，其中为了消除实际信号中的噪声影响，在微分项中增加了平滑因子N。

^{MATLAB中带有平滑项的数字PID模块}

使用MATLAB中 Embed Coder Quick Start可以产生PID控制器的C语言代码。详细的操作过程可以直接在MATLAB中按照提示一步一步进行。所产生的C语言的代码如下图所示：

^{MATLAB产生的离散PID的C语言代码}

当然，上述产生的C代码还只是一个示例，相对比较简单。可以将它拷贝到具体的单片机编译工程文件中作为控制子程序加以应用。

延伸讨论对于系统框图的正确应用需要能够系统学习或者自学关于信号与系统、控制理论方面的知识。通过建立实际系统和算法的框图，再借助于MATLAB等先进的软件仿真平台，可以对控制对象的算法及其参数做精确的测试和优化。并在此基础上开发出性能更加鲁棒可靠的算法。

但在实际中，同学们往往发现很多情况下，这种基于模型建立的算法在实际应用中会遇到很大的限制。就像在今年智能车竞赛全国总决赛的技术交流会上，很多同学总结到，越是简单的算法，在比赛中越是有优势。

^{智能车竞赛全国总决赛技术交流会}

造成理论学习中的内容在竞赛实践应用中的尴尬局面的原因主要包括以下几点：

（1）在车模竞赛中，影响车模运行因素很多，特别是一些非线性环节所造成的影响很大，比如赛道的摩擦力、驱动电机功率饱和、赛道传感器的范围以及非线性、外部环境的噪声等等。这些原因都会使得系统模型建立非常困难，而简化后的线性模型又无法准确描述实际系统；

（2）竞赛的任务相对单一，系统软件和控制算法相对简单，系统可靠性要求不高。很多控制参数的优化，以及系统的调试在使用试凑方法还可以解决。因此，对于系统数学建模和仿真方面的工作就显得不那么重要了；

（3）现在参加竞赛的同学往往是低年级的同学，对于控制系统的建模分析方面的基础知识不足；

尽管如此，还是希望参加智能车竞赛的同学们，能够在实践环节中，在掌握了一些实际工具和设计技能之后，能够有意和可能理论知识相结合。激发出更多的探究兴趣，为今后更加复杂的工程挑战以及系统理论研究打下牢靠的基础。