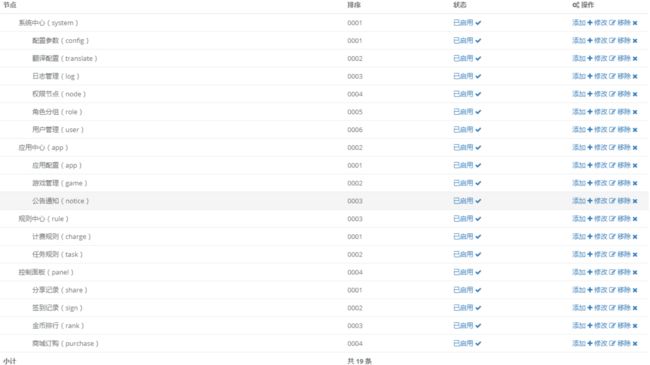
数据库无限级分类
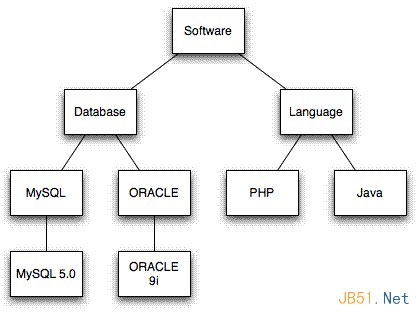
程序设计中常使用树型结构来表征某些数据的关联关系,如上下级、栏目结构、商品分类、菜单、回复等。
分类的层级关系可以表述为一父多子的继承关系,对应数据结构中的树。因此,分类问题可以转换为如何在数据库中存储一棵树。
通常树形结构需借助数据库完成持久化,在关系型数据库中由于是以二维表的形式记录数据信息,因此不能直接将树形结构存入,必须设计合适的Schema及对应的增删改查算法以实现在关系型数据库中存储和操作。
理想的树形结构应该具备
- 数据存储冗余度小且直观性强
- 检索遍历过程简单高效
- 节点增删改查操作简单高效
树形结构在关系型数据库中常用的存储方式
- 双亲表
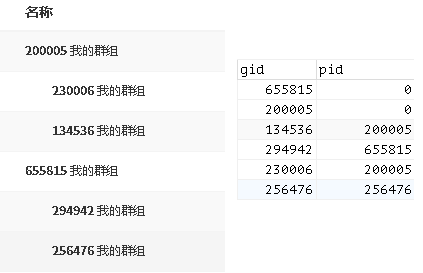
双亲表主要通过记录节点唯一id以及父节点pid来维护树的结构关系
`gid` int(11) unsigned DEFAULT '0' COMMENT '唯一编号 ',
`pid` int(11) unsigned DEFAULT '0' COMMENT '上级编号',
双亲表有什么优缺点呢?
- 优点在于可以方便的对树的节点进行增删改查等操作,而且涉及变动的记录较少。
- 缺点是对于无差别子孙集合的获取需要递归,获取节点从根节点开始的路径也需要递归追溯,因此时间开销较大。
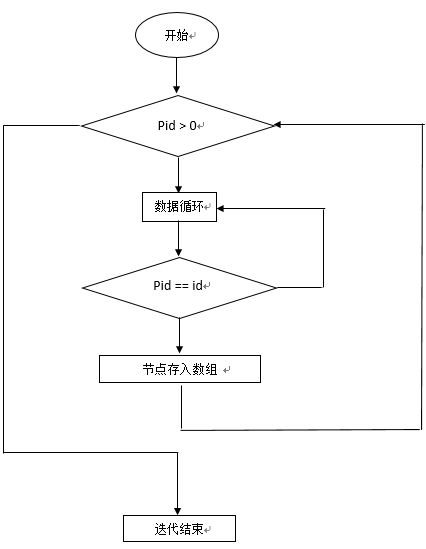
什么是递归函数呢?
递归函数是函数自身调用自身,但必须在调用自身前有条件判断,否则将无限调用下去。
递归算法解决问题的特点
- 递归就是函数或方法里调用自身
- 在使用递增策略时,必须有一个明确的递归结束条件,称为递归出口。
- 递归算法解题显得简洁,但运行效率较低,一般不提倡使用递归算法设计程序。
- 在递归调用过程中系统为每一层的返回点、局部变量等都会开辟了栈来存储
- 递归层级过深容易造成栈溢出
PHP实现递归函数有三种基本的方式:全局变量、引用、静态变量
- 使用引用做参数
&
什么是引用呢?引用是指两个不同名字的变量指向同一块存储地址,本来每个变量都是各自的存储地址,赋值删除操作时各行其道,使用&取地址符后可以使两个变量共享同一块地址。
函数之间本来时各行其道,即使是同名函数。递归函数将引用作为参数形成一个桥梁使两个函数之间进行数据共享,虽然两个函数貌似操作的是不同地址,但实际上操作的是同一块内存地址。
例如:将数据格式化为树形结构
function tree($list, $pid="pid", $pk="id", $child="child"){
foreach($list as $k=>$v){
$list[$v[$pid]][$child][$v[$pk]] = &$list[$v[$pk]];
}
return isset($list[0][$child]) ? $list[0][$child] : [];
}
function tree($list, $pid="pid", $pk="id", $child="child"){
$ret = [];
foreach($list as $k=>$v){
if(isset($list[$v[$pid]])){
$list[$v[$pid]][$child][] = &$list[$v[$pk]];
}else{
$ret[] = &$list[$v[$pk]];
}
}
return $ret;
}
- 利用全局变量
global
利用全局变量完成递归,全局变量global在函数内申明变量不过是外部变量的同名引用,变量的作用范围仍然在本函数范围内。改变变量的值,外部同名变量的值自然也会改变。但一旦使用了取地址符&,同名变量不再是同名引用。
- 利用静态变量
static
利用静态变量static使用到递归函数时,static的作用仅在第一次调用函数时对变量进行初始化,并保留变量值。因此,将static应用到递归函数作用可想而知。在需要作为递归函数间作为“桥梁”的变量利用static进行初始化,每次递归都会保留“桥梁变量”的值。
例如:根据子类ID获取所有父类
/*根据子类ID获取所有父类*/
function getParents($list, $id=0, $level=0, $clear=true){
static $ret = [];//声明静态数组用于存储最终结果
//首次进入清除上次调用函数留下的静态变量的值,进入深一层循环时则不要清除。
if($clear==true) $ret = [];
//循环遍历
foreach($list as $k=>$v){
if($id == $v['id']){
$v["level"] = $level;
$ret[] = $v;
getParents($list, $v["pid"], $level-1, false);
}
}
return $ret;
}
例如:根据父类ID获取所有子类
function getChildren($list, $pid=0, $level=0, $clear=true){
static $ret = [];//声明静态数组存储结果
//对刚进入函数要清除上次调用此函数后留下的静态变量的值,进入深一层循环时则无需清除。
if($clear==true) $ret = [];
foreach($list as $k=>$v){
if($pid == $v["pid"]){
$v["level"] = $level;
$ret[] = $v;
getChildren($list, $v["id"], $level+1, $clear=false);
}
}
return $ret;
}
递归函数重点是如何处理函数调用自身是如何保证所需要的结果得以在函数间合理传递,当然也无需函数之间传值得递归函数。
例如:递归获取某节点下的所有子孙节点,返回一个多维数组。
function tree($list, $pid=0, $pk="id", $label="child"){
$children = [];
//循环所有数据查找指定ID的下级
foreach($list as $k=>$v){
if($pid == $v[$pk]){//找到下级
$children[$v[$pk]] = $v;//保存后继续查找下级的下级
unset($list[$k]);//去掉自己,因为自己不可能是自己的下级
// 递归查找将找到的下级放入children数组的child字段中
$children[$v[$pk]][$label] = tree($list, $v[$pk], $pk, $label);
}
}
return $children;
}
例如:使用递归获取多维数组的树形结构
/*由父类获取全部子类并得到多维数组的树形结构*/
function tree($list, $pid=0, $pk="id", $label="child"){
$arr = [];
foreach($list as $k=>$v){
if($pid == $v[$pk]){
$v[$label] = tree($list, $v[$pk], $pk, $label);
$arr[] = $v;
}
}
return $arr;
}
例如:使用静态变量根据父类获得全部子类得到一个二维数组
function tree($list, $pid=0, $level=0, $pk="id"){
static $arr = [];//定义静态数组
//第一次遍历时找到pid=0的节点
foreach($list as $k=>$v){
//pid为0的节点对应的是第一级也就是顶级节点
if($v[$pk] == $pid){
$v["level"] = $level;
$arr[] = $v;//将数组放入静态变量
unset($list[$k]);//将节点从数组中移除以减少后续递归消耗
tree($list, $v[$pk], $level+1, $pk);//递归查找父节点为本节点ID的节点,层级自增。
}
}
return $arr;
}
例如:使用引用传值的方式获取多维树形结构
引用&是一个非常巧妙的方式,不用像递归那样循环多次,思路是将数据以主键为索引重新排列,排序后找到根节点pid=0,并将其放入一个全新的数组。注意,这里存放的并非简单的赋值,而是引用之前的地址。
function tree($list, $pk="id", $pid="pid", $child="child", $root=0){
$pick = [];
//循环重新排列
foreach($list as $item){
$pick[$item[$pk]] = $item;
}
$tree = [];
foreach($pick as $k=>$v){
//判断是否为根节点,若是则将根节点数组的引用赋给新数组
if($v[$pid] == $root){
$tree[] = &$pick[$k];//根节点直接把地址放入新数组
}else{
// 子类数组赋值给父类数组中键为child的数组
$pick[$v[$pid]][$child][] = &$pick[$k];//不是过根节点的则将自己的地址存放到父级的child节点中
}
}
return $tree;
}
- 层次表
层次表通过记录节点id以及从根节点起到目标节点的路径path来存储树形结构的关系,其中路径path由节点编号id的序列组成。因为涉及到路径的编码规则,所以在实现时有多种不同形式。
比如,在节点较少编号较短的情况下节点路径可以考虑直接使用无层次差别的节点编码。在节点较多时可以考虑以层次level为基准对节点进行编码,节点的唯一编码由【层级level】+【层次节点path】组成。即使路径使用无层次差别的同一节点编号,也可以使用“层次级别”来标识节点深度,以便更快的查询特定深度级别的节点。
层次表的优点在于无需递归就可以方便地实现常用树形结构的查询,缺点是首先对于更改树形层次结构时,尤其时更改位于较高层次节点时会引起大量记录的修改,这个时间开销十分巨大。其次,路径的表达也有一些棘手的问题,路径字段的长度设置会限制了树形结构的层次深度。节点的编码方式也可能影响到每个层次上节点的最大数量。
例如:查询指定节点的所有下级
SELECT * FROM nodes WHERE path LIKE "1,%"
例如:查询指定节点的直属下级
SELECT * FROM nodes WHERE path LIKE "1%"
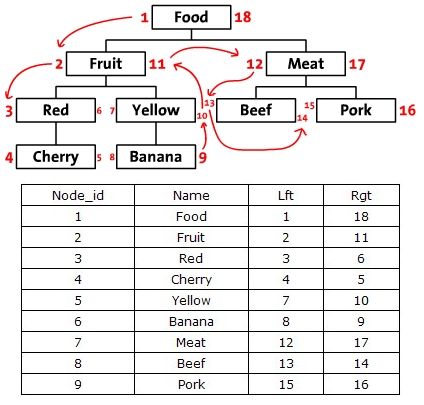
- 先根遍历树表
先根遍历树表的主要思想是通过记录先根遍历中的第一次访问节点时的次序号(左值,lft)与回溯时第二次访问的次序号(右值,rgt)来维护树形结构的层次关系。
由先根遍历的概念可知,子节点的左值必须大于父节点的左值,子节点的右值必然小于父节点的右值。结合排序操作可以很容易的在不适用递归的情况下对树形数据进行查询操作。
- 扩展的线索二叉树表
扩展的线索二叉树表方式是在双亲表的基础上进行改变,增加了按深度搜索顺序的节点访问序号sn。这种方式可以看作是双亲表与先根遍历树方式的折中方案。
常见实现方式:邻接表(The Adjacency List Model,邻接列表模型)、预排序遍历树(MPTT)
- 继承关系驱动的Schema设计
- 基于左右值编码的Schema设计
继承关系驱动的Schema设计
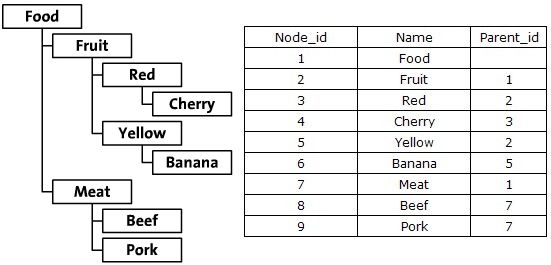
对树形结构最直观的分析莫过于节点之间的继承关系,通过显式地描述某个节点的父节点,从而能够建立二维的关系表,这种方案的属性结果表通常设计为{node_id, parent_id}。
- 设计优点
设计和实现自然而然,非常直观和方便。
- 设计缺点
由于直接记录了节点之间的继承关系,因此对树形结构的任何增删改查操作都将是低效的,这主要归根于频繁的递归操作,递归过程不断地访问数据库,每次数据库IO都是会有时间开销的。
递归中的SQL查询会导致负载变大,特别是需要处理比较大型的树状结构时,查询语句会随着层级的增加而增加。
例如:获取某子类其它所有父级的名称
SELECT
t1.name AS lv1name,
t2.name AS lv2name,
t3.name AS lv3name
FROM nodes AS t1
LEFT JOIN nodes AS t2 ON t2.pid=t1.id
LEFT JOIN nodes AS t3 ON t3.pid=t2.id
WHERE 1=1
AND t3.id = 100
例如:根据指定节点获取所有下级节点
delimiter /
DROP FUNCTION IF EXISTS `nodes`.`getChildren` /
CREATE FUNCTION `getChildren`(root_id INT)
RETURNS VARCHAR(255)
BEGIN
DECLARE ret VARCHAR(255);
DECLARE ids VARCHAR(255);
SET ret = '#';
SET ids = CAST(root_id AS CHAR);
WHILE ids IS NOT NULL DO
SET ids = CONCAT(ret, ',', ids);
SELECT GROUP_CONCAT(id) INTO ids FROM nodes WHERE 1=1 AND FIND_IN_SET(pid, ids)>0;
END WHILE;
RETURN ret;
END
SELECT * FROM nodes WHERE 1=1 AND FIND_IN_SET(id, getChildren(1))
适用场景
在树形结构规模较小的情况下,可借助于缓存接置来优化,将树形结构存入内存进行处理,避免直接对数据库IO操作的性能开销。
最佳实践
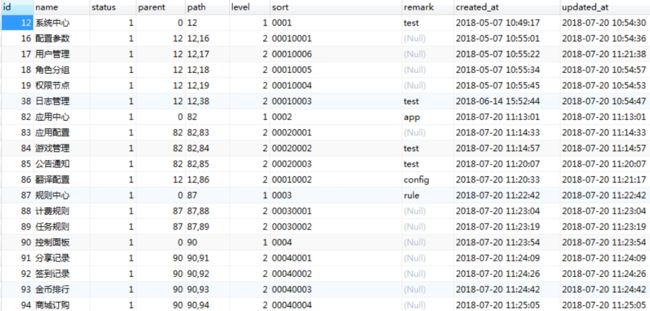
邻接表主要依赖于pid字段,用于指向上级节点,将相邻上下级节点连接,id为自动递增。
CREATE TABLE `nodes` (
`id` int(11) unsigned NOT NULL AUTO_INCREMENT,
`name` varchar(30) COLLATE utf8mb4_unicode_ci DEFAULT '' COMMENT '名称',
`pid` int(11) unsigned DEFAULT '0' COMMENT '父级节点',
`path` varchar(255) COLLATE utf8mb4_unicode_ci DEFAULT '0' COMMENT '节点路径',
`level` tinyint(3) unsigned DEFAULT '1' COMMENT '节点层级',
`sort` varchar(30) COLLATE utf8mb4_unicode_ci DEFAULT '' COMMENT '排序值',
`status` tinyint(1) unsigned DEFAULT '1' COMMENT '状态 0禁用 1启用',
`remark` varchar(255) COLLATE utf8mb4_unicode_ci DEFAULT '' COMMENT '备注',
`created_at` timestamp NULL DEFAULT NULL COMMENT '创建时间',
`updated_at` timestamp NULL DEFAULT NULL COMMENT '更新时间'
PRIMARY KEY (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=0 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_unicode_ci COMMENT='节点';
- 优化设计
- 根据父节点递归
pid
当查询指定深度节点时,需要通过递归来逐层展开,才能获取到所有该层的节点,然后在其中进行查询,既浪费时间又浪费空间。
- 保存节点路径
path和深度level
SELECT * FROM `nodes` WHERE `path` LIKE "1,3%"
这样做的目的是通过增加冗余信息来提高检索速度,同时冗余信息非常容易维护,所以不会因为操作不慎而导致信息不一致。
设想一下你要对树增加/移动/删除一个节点,原本一条SQL语句就能完成的事情现在还是一条SQL语句就能完成,就算不依赖事务也绝对不会导致信息不一致。
- 进一步优化
在树形结构中,为方便排序且提高查询效率,设计了path字段,用于记录树形的链条节点。为了进一步提高查询效率,可将每个节点的主键id回写入路径path中,这样做避免使用CONCAT(path,',',id) AS abspath的方式,但同时也存在相应弊端。
这样做的好处是直接通过ORDER BY path ASC即可对树形结构排序,但是当出现需要自定义排序的时候,问题出现了。若采用普通设置一个sort且以自然数的形式,排序时采用ORDER BY path ASC, sort ASC的做法,其结果又是无法得到想要不同层级的排序。
排序字段sort中需要反映中层级结构,且能进行层级内与层级间的排序。为此使用sort编码的方式,每个排序值以4位数字进行编码,纵向层级依次向后拓展。很明显,这种规则存在这硬伤,适用的范围可想而知。使用时限制仍旧很多,相对来说解决了一定的问题,但同时也带来风险。
- 编码法
sort
每级分类递增4位数字,既定每级分类数目限定在10000个。
一级:0001,0002,0003...
二级:00010001,00010002,00010003...
三级:000100010001,000100010002,000100010003....
...
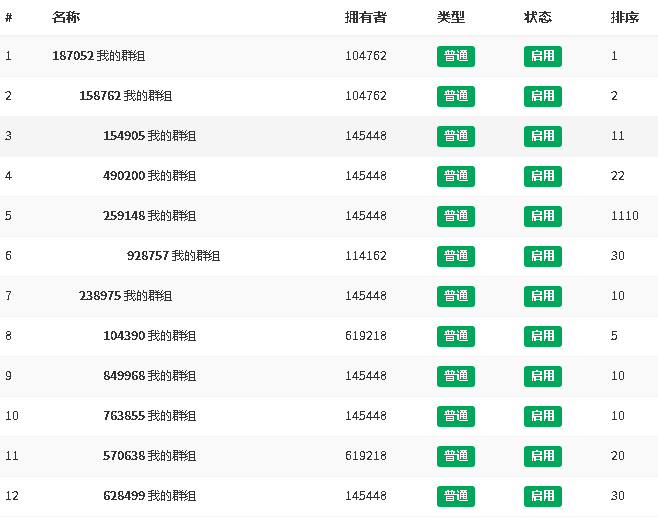
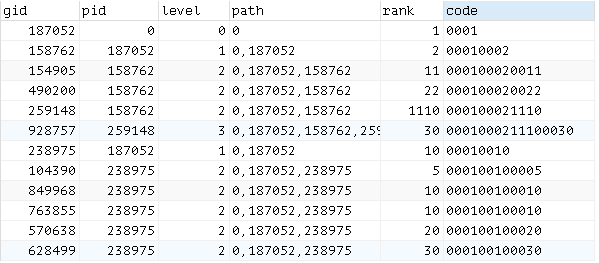
可在数据表设置添加两个字段rank排序值与code编码值,rank排序值为用户自定义设置的数值,code编码值则使用父级的编码值拼接上自己的4位数字编码值。
$code .= str_pad($rank, 4, "0", STR_PAD_LEFT);
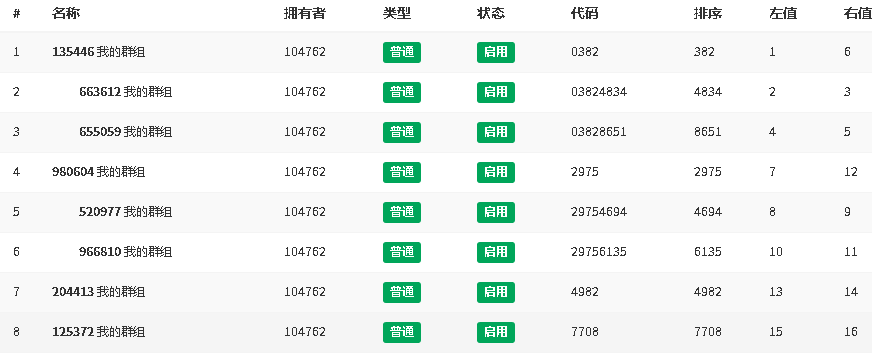
SELECT `gid`,`pid`,`level`,`path`,`rank`,`code` FROM web_group ORDER BY code ASC
基于左右值编码的Schema设计
在基于数据库的应用中查询的需求总是要大于删除和修改的,也就是说读操作往往会大于写操作。为了避免对树形结构查询时的递归操作,需要设计一种全新的无递归查询、无限分类的方案。
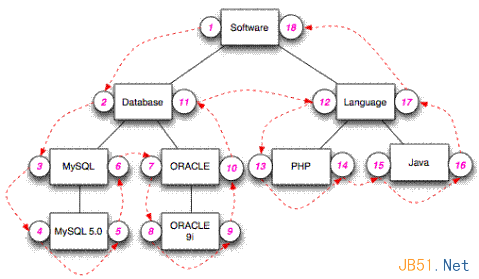
基于左右值编码的Schema设计的算法采用了预排序遍历树算法MPTT(Modified Preorder Tree Traversal),此算法在第一种方式的基础上,给每个节点增加左右数字(lft和rgt),用于标识节点的遍历顺序。
基于树形结构的前序遍历的方案的属性结果表通常设计为{node_id, lft, rgt},由于left和right在SQL中具有特殊含义,所以使用lft和rgt来标识列。
基于左右值编码的Schema设计中并没有保存保存父子节点的继承关系,根据箭头的移动顺序就是对树进行前序遍历的顺序,整棵树的结构通过左值和右值存储了下来。
预排序遍历树算法的数据结构中重点关注的是左右值的维护及查询的便捷性。
-
lft表示节点的左值 -
rgt表示节点的右值 -
level表示节点所在层级
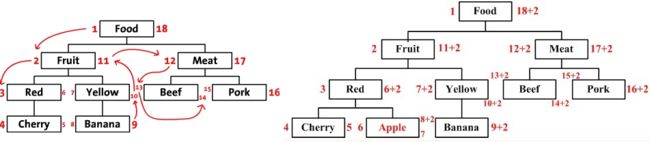
添加节点
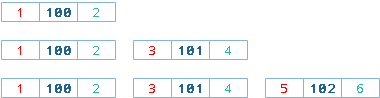
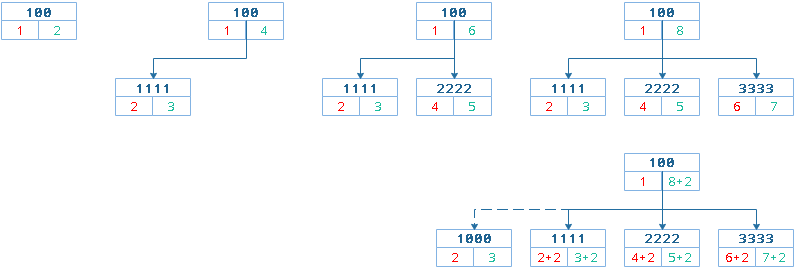
添加节点时如果不考虑指点节点的顺序而采用从左到右的自然顺序时,只需要从左向右依次插入即可。
从左至右依次插入顶级节点时,待插入节点的左右值与顶级节点中最大右值相关。
- 待插入顶级节点左值 = 顶级节点最大右值 + 1
- 待插入顶级节点右值 = 顶级节点最大右值 + 2
从左至右依次插入子节点时,待插入子节点的左右值与父级节点的右值相关。
- 待插入子节点左值 = 父级节点右值
- 待插入子节点右值 = 父级节点右值 + 1
添加节点时如果需要指定节点的顺序,此时每个节点都需要设置一个所在层级的排序值,相当于索引值。
此时添加节点前首先需要考虑的时添加节点的位置,也就是需要在当前层级中找到与待插入节点排序值最接近的那个参照节点。在参照节点的左侧或右侧进行插入,与之同时需要考虑最左侧与最右侧两种情况。
整体而言,思路是先找到参照节点,然后为目标节点腾出位置,也就是将参考节点之后的所有节点进行左右值更新为其腾出位置,最后才是插入目标节点。
这里重点就指定排序值的方式插入为例加以说明
节点定位
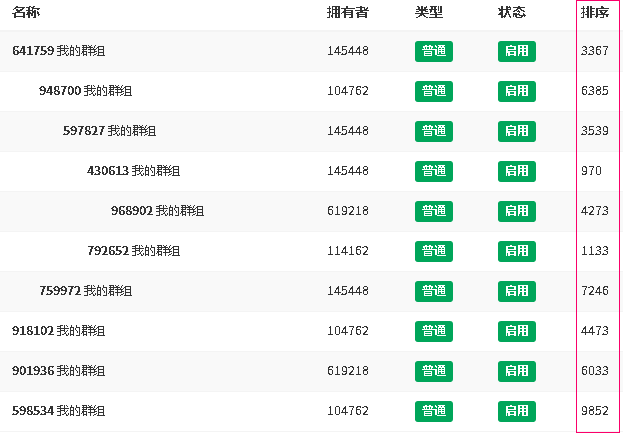
如何新增节点呢?首先需要有一个参考点,也就是你准备在树中哪个位置插入节点,是参考节点左侧、右侧还是下面呢,当然这里并不会考虑上面,你懂的!简单来说,就是如何定位参考节点的位置,结合上面的做法,可以在表中新增排序值rank字段,表示每个节点在所在层级level中的位置。注意是当前所在层级,而非树结构整体中的位置。如果要标识当前节点在树结构中的位置,可以采用编码法搞定。
这里的排序值采用升序的方式,也就是小的在上面大的在下面,相当于排行榜。
使用当前层级的排序值rank重点是为了定位节点,根据排序值的大小,可以找到目标位置。接下来应该怎么做呢?思路是这个样子的:当添加某层级节点并设置排序值后,根据排序值查找当前层级(也就是具有相同父节点的子节点)中最接近的节点,用SQL语句表达一下。
例如:获取父级为10的子节点中,排序值与8000最接近的子节点。
SELECT * FROM nodes WHERE 1=1 AND pid=10 ORDER BY ABS(`rank`-8000) ASC LIMIT 0,1
获取到了有什么用呢,划重点再强调下定位,找到目标节点后,比较新节点与目标节点的排序值,根据升序排列的规则,如果新节点的排序值小于目标节点的排序值,表示新节点位于目标节点的左侧或者说是前面,换种说法也就是新节点是目标节点的同辈兄弟节点之前的元素。只是在树结构中看到的是左侧,而在排序数值上看到的是上面,这些就不纠结了。反之亦然...
如果没有最接近的子节点,那么不用说,它就是第一个节点,这个最好办。
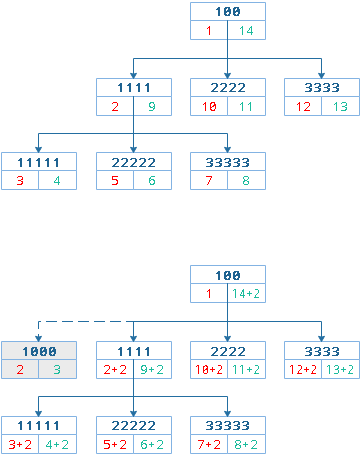
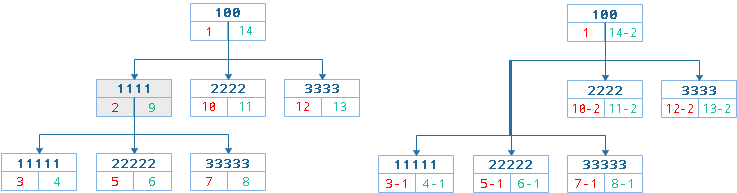
最左侧
如果同辈中没有节点,此时会插入到子节点的最左端,此时参考点是父节点。
- 参考节点:父节点
- 腾出空间:所有比父节点左值大的节点的左右值均需要增加2
- 目标节点:
- 待插入节点的左值 = 父节点的左值 + 1
- 待插入节点的右值 = 父节点的左值 + 2
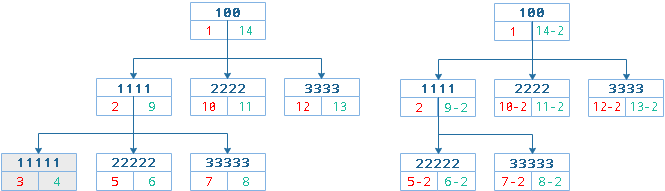
相对左侧
- 参考节点:待插入节点排序值为2221,获取参考点的排序值为2222,目标节点位于参考节点相对左侧。
- 腾出空间:大于等于参考字节左值的节点的左值增加2, 大于等于参考字节右值的节点的右值增加2。
- 目标节点:目标节点左值等于参考节点左值,目标节点 右值等于参考节点右值
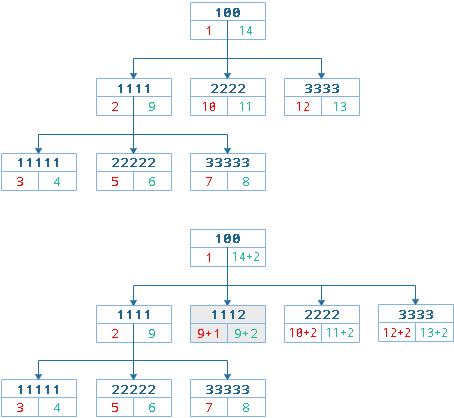
相对右侧
- 参考节点:待插入节点排序值为1112,获取参考点的排序值为1111,目标节点位于参考节点相对右侧。
- 腾出空间:大于参考节点右值的节点的左右值都增加2
- 目标节点:目标节点左值等于参考节点右值增加1,目标节点 右值等于参考节点右值增加2.
插入节点的整体思路是:变更所有受影响的节点并给新节点腾出空位置
- 左侧插入节点
有了参考点之后,首先需求获取目标节点,然后变更所有受影响的节点。那么插入节点时哪些节点会受到影响呢?根据前置排序遍历算法MTPP节点遍历的路径来看,比目标节点左值大的节点都会受到影响,受到什么样的影响呢?这里要分两种情况来看,第一种时目标节点前面没有节点也就是说目标节点实际上就是头节点,第二种情况是目标节点前面还有同辈兄弟节点。
- 目标节点是头节点
目标节点是头节点,很好做,也就是插入的节点就是目标节点,目标节点后移一位。具体来说,首先目标节点及其后续节点的左值加1右值加2,新增节点左右值等于目标节点左右值。
所有左节点比目标节点大的都增加2, 所有右节点比目标节点大的都增加2,计算新节点的左右值并插入。
LOCK TABLE nodes WRITE;
SELECT @left := lft FROM nodes WHERE 1=1 AND id = 12;
UPDATE nodes SET lft = lft + 2 WHERE 1=1 AND lft > @left;
UPDATE nodes SET rgt = rgt + 2 WHERE 1=1 AND rgt > @left;
INSERT INTO nodes(name, lft, rgt) VALUES("charqui", @left+1, @left+2);
UNLOCK TABLES;
- 右侧添加节点
LOCK TABLE nodes WRITE;
SELECT @right := rgt FROM nodes WHERE 1=1 AND 'name' = 'Cherry';
UPDATE nodes SET lft = lft + 2 WHERE 1=1 AND lft > @right;
UPDATE nodes SET rgt = rgt + 2 WHERE 1=1 AND rgt > @right;
INSERT INTO nodes(name, lft, rgt) VALUES("Apple", @right+1, @right+2);
UNLOCK TABLES;
例如:每次插入节点后查看验证
SELECT
CONCAT( REPEAT(" ", (COUNT(parent.name)-1)), node.name ) AS name
FROM nodes AS node, nodes AS parent
WHERE 1=1
AND node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.name
ORDER BY node.lft
查询节点
采用左右值编码的设计方案,在进行类别树的遍历时只需进行两次遍历,消除了递归,加之查询条件都是以数字进行比较,效率极高。类别树的记录数量越多执行效率越高。
计算某个节点的子孙节点总数,不包含自身节点。
子孙总数 = (右值 - 左值 - 1)/ 2
SELECT (rgt - lft - 1)/2 AS leaves FROM node WHERE name="database";
计算某个节点的子孙节点总数,包含自身节点。
子孙总数 = (右值 - 左值 + 1)/ 2
SELECT (rgt - lft + 1)/2 AS leaves FROM node WHERE name="database";
获取节点在树中所处的层数
SELECT COUNT(1) AS level FROM node WHERE 1=1 lft<=2 AND rgt>=11
获取当前节点所在路径
SELECT * FROM node WHERE 1=1 AND lft<=2 AND rgt>=11 ORDER BY lft ASC;
判断是否为叶子节点,即子孙节点个数为0。
是否为叶子节点 = (右值 - 左值 - 1) / 2 < 1
SELECT * FROM node WHERE 1=1 AND (rgt - lft - 1) / 2 < 1;
判断是否有子节点
是否有子节点 = (右值 - 左值)> 1
获得某个节点下的所有子孙节点
要使用左右值表示的树首先必须标识要检索的节点
例如:获取Database的子树,则必须仅选择左值在2到11之间的节点
SELECT * FROM nodes WHERE lft BETWEEN 2 AND 11 ORDER BY lft ASC
如果查询一棵树后要像递归一样显示这颗树,则必须向查询中添加排序子句。如果要从表中添加和删除表,则表可能不会处于正确的顺序。因此,需要按照左值排序。
SELECT * FROM nodes WHERE 1=1 AND lft BETWEEN 2 AND 11 ORDER BY lft ASC;
为了显示树状结构,子级的缩进应该比父级多一点,应该怎么做呢?
例如:获取节点的所有子节点数量与所属层级
SELECT
a.name,
a.lft,
a.rgt,
(a.rgt - a.lft - 1)/2+'' AS children,
(SELECT COUNT(1) FROM nodes AS b WHERE 1=1 AND b.lfta.rgt) AS level
FROM nodes AS a
ORDER BY a.lft
获取祖先节点个数,同时也是自身层级数。
SELECT COUNT(1) AS cnt FROM node WHERE 1=1 AND lft<4 AND rgt>5
查询所有无分支的节点:右值 = 左值 + 1
SELECT * FROM nodes WHERE 1=1 AND rgt = lft + 1;
删除节点
删除叶子节点
这里的删除节点指的是叶子节点,也就是没有下级节点的节点。
操作思路
- 获取目标节点的左右值
SELECT @left := lft, @right := rgt FROM nodes WHERE 1=1 AND name = "xxx";
- 获取目标节点的间距值并加1
间距值 = 目标节点右值 - 目标节点左值 + 1
@width := rgt - lft + 1
- 删除目标节点
DELETE FROM nodes WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
- 更新目标节点右侧后续节点的右值
将右值大于目标节点右值的所有节点的右值减去间距值
UPDATE nodes SET rgt = rgt - @width WHERE 1=1 AND rgt > @right;
- 更新目标节点右侧后续节点的左值
将左值大于目标节点右值的所有节点的左值减去间距值
UPDATE nodes SET lft = lft - @width WHERE 1=1 AND lft > @rgt;
完整代码
LOCK TABLE nodes WRITE;
SELECT @left := lft, @right := rgt, @width := rgt - lft + 1 FROM nodes WHERE 1=1 AND name = "Beef";
DELETE FROM nodes WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
UPDATE nodes SET rgt = rgt - @width WHERE 1=1 AND rgt > @rgt;
UPDATE nodes SET lft = lft - @width WHERE 1=1 AND lft > @rgt;
UNLOCK TABLES;
删除父节点
- 获取目标节点左右值
SELECT @lft:=lft, @rgt:=rgt FROM nodes WHERE 1=1 AND name="xxx";
- 计算目标节点的左右间距值并加1
@width:= rgt - left + 1
- 删除目标节点
DELETE FROM nodes WHERE lft = @lft;
- 更新目标节点的子孙节点的左右值,子孙节点的左右值均减去1。
UPDATE nodes SET lft = lft -1, rgt = rgt - 1 WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
- 更新目标节点右侧后续节点的右值,后续节点右值减去2。
UPDATE nodes SET rgt = rgt - 2 WHERE 1=1 AND rgt > @rgt;
- 更新目标节点右侧后续节点的左值,后续节点左值减去2。
UPDATE nodes SET lft = lft - 2 WHERE 1=1 AND lft > @rgt;
完整代码
LOCK TABLE nodes WRITE;
SELECT @lft:=lft, @rgt:=rgt,@width:=rgt - left + 1 FROM nodes WHERE 1=1 AND name="xxx";
DELETE FROM nodes WHERE lft = @lft;
UPDATE nodes SET lft = lft -1, rgt = rgt - 1 WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
UPDATE nodes SET rgt = rgt - 2 WHERE 1=1 AND rgt > @rgt;
UPDATE nodes SET lft = lft - 2 WHERE 1=1 AND lft > @rgt;
UNLOCK TABLES;
移除父节点及其子孙节点
移除父节点表示删除父节点以及其分支子孙节点
- 获取目标节点的左右值
SELECT @lft:=lft, @rgt:=rgt FROM nodes WHERE 1=1 AND name="xxx";
- 计算节点间距
@width = rgt - lft + 1;
- 删除父节点及其子孙节点
DELETE FROM node WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
- 更新目标节点右侧后续节点的右值
UPDATE nodes SET rgt = rgt - @width WHERE 1=1 AND rgt > @rgt;
- 更新目标节点右侧后续节点的左值
UPDATE nodes SET lft = lft - @width WHERE 1=1 AND lft > @rgt;
完整代码
LOCK TABLE nodes WRITE;
SELECT @lft := lft, @rgt := rgt, @width = rgt - lft + 1 FROM nodes WHERE 1=1 AND name="xxx";
DELETE FROM nodes WHERE 1=1 AND lft BETWEEN @lft AND @rgt;
UPDATE nodes SET rgt = rgt - @width WHERE 1=1 AND rgt > @rgt;
UPDATE nodes SET lft = lft - @width WHERE 1=1 AND lft > @rgt;
UNLOCK TABLES;
移动节点
移动节点中的目标节点可分为两种情况,一种是目标节点为叶子节点即没有子节点的节点,第二种情况是父节点即带子节点的节点。从方位上来说,移动节点可以根据层级分为上级移动到下级、下级移动到上级。
移动节点可分为两个步骤来完成,首先是剔除原节点,其次是添加节点。移动节点的难题在于目标节点与目标节点之外的数据如何分割的问题,一种思路是采用临时表,使用变量替换的方式,将目标节点剔除后保存到临时表中,然后更新原来的树,接着将目标节点插入树并更新节点。
优化方案
设计优点
在消除递归操作的前提下实现了无限极分类,由于查询条件是基于整型数字的比较,因此效率很高。
设计缺点
节点的添加、删除、修改代价较大,将会设计到表中多方面数据的改动。
预排序遍历树算法最大优势是提升了读的性能,但牺牲了写的性能,而且写的时候必须锁表,因为新增节点时要更新大量节点的左右值。
优化方案
非连续性与排序遍历算法是预排序遍历算法的改进版,其目的是让新增节点时不用更新其它节点的左右值,这样就不会牺牲写的性能,那么如何实现呢?
由于预排序遍历树算法只是对各个节点进行了顺序且连续的整数型预排序,而非连续型预排序遍历树算法是对各个节点进行顺序的非连续的实数型预排序。
在初始化根节点时,为其设置一个比较大的实数范围,如lft=1000000 rgt=9000000,然后新增子节点时可以划分实数范围的一个数据段。
只需要将左右值的字段类型定义为双精度double。当新增节点时,只需要将新节点放到空位上,并设置左右值为小数,其它节点都不用更新左右值。
未完待续...