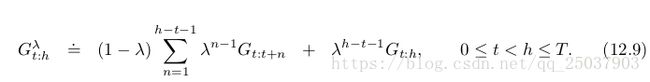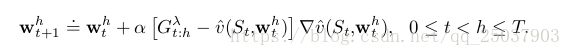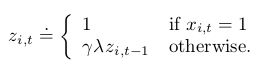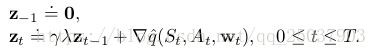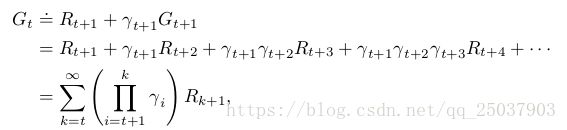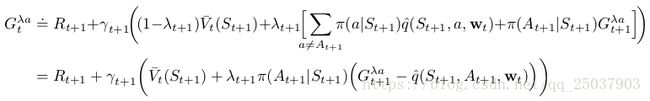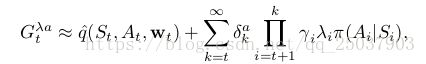强化学习(RLAI)读书笔记第十二章资格迹(Eligibility Traces)
资格迹是强化学习算法中的一个基本机制。比如很流行的![]() 其中的
其中的![]() 指的就是资格迹的使用。基本上所有的TD算法都能够和资格迹进行组合从而得到一个更通用的算法。资格迹把TD和MC方法统一了起来。当TD算法和资格迹进行组合使用时,得到了一组从一步TD延伸到MC算法的算法家族。一般中间部分的算法效果比两端的好。资格迹同样提供了一种在线continuing形式的问题上使用MC算法的实现方式。
指的就是资格迹的使用。基本上所有的TD算法都能够和资格迹进行组合从而得到一个更通用的算法。资格迹把TD和MC方法统一了起来。当TD算法和资格迹进行组合使用时,得到了一组从一步TD延伸到MC算法的算法家族。一般中间部分的算法效果比两端的好。资格迹同样提供了一种在线continuing形式的问题上使用MC算法的实现方式。
之前第七章使用n步TD法已经组合过了TD法和MC方法,但是资格迹的方式更加的优雅而且有很大的计算优势。这个机制使用了一个短期记忆的向量,资格迹![]() ,与长期的权重w平行。大致的思想是当w的某个分量参与了一个估计值的计算,那么z的相对应的部分就增大,之后慢慢减小。当对应的z分量减小为0之前有一个不为零的TD error,那么w对应的部分就会进行更新。而资格迹消减的系数为
,与长期的权重w平行。大致的思想是当w的某个分量参与了一个估计值的计算,那么z的相对应的部分就增大,之后慢慢减小。当对应的z分量减小为0之前有一个不为零的TD error,那么w对应的部分就会进行更新。而资格迹消减的系数为![]() 。
。
资格迹相对于n步TD算法的计算优势在于只需要一个资格迹向量而不需要像n步算法一样要保存过去n个状态的特征向量。而学习的过程也连续而均匀均匀分布而不是延迟到获得episode末尾的反馈值为止。另外,学习过程可以每一步都进行从而立马就会影响到下一状态的行为而不是等到n步之后才能更新。
有些算法需要等待之后状态的返回值来进行学习,比如MC算法和n步TD算法。这种基于从被更新状态往前观察的机制叫做forward views。forward views一般都实现起来比较复杂因为需要考虑当前无法获得的之后状态的反馈值。而这一章我们介绍的算法将要能够使用当前的TD error并且通过资格迹使用先前访问过的状态来获得和forward views几乎一样的更新。这种形式叫做backward views。
像往常一样先介绍状态值函数估计,然后延伸到动作值函数和control算法。主要关注线性函数逼近,因为它使用了资格迹的结果会变得更好。线性的结果也可以应用到表格型和状态集成里去。
12.1 The  -return
-return
第七章定义了n步反馈为前n个奖励加上第n步状态的估计值,每一项都加上discounted系数,也就是:
![]()
现在考虑更新目标不仅仅是一个n步反馈值,而是不同的n的n步反馈的平均值。比如一个两步反馈的一半加上一个四步反馈的一半组合成的一个新的反馈值。任意的n步反馈的集合可以通过这种形式进行平均,只要最终的系数和为1。合成的反馈值能够和单个的n步反馈一样处理TD error因此能够作为一个保证算法收敛的更新目标。这种平均的形式能够得到一系列新的算法。比如可以通过将一步TD的反馈和无穷步反馈MC反馈进行平均得到一种新的组合TD算法和MC算法的方式。理论上甚至可以将基于模型得到的DP反馈和实际经验得到的反馈进行简单的结合。
这种平均更简单的更新分量的更新叫做复合更新。它的backup diagrams如右图。一个复合更新只能够等待它 的分量中最长的部分更新得到结果之后才能够进行计算。比如右图中的两个更新必须等待t+4的那个更新得到了之后才能计算平均的复合更新。所以使用的时候应该限制最长n步反馈的n,防止每次更新需要过长的等待时间。
的分量中最长的部分更新得到结果之后才能够进行计算。比如右图中的两个更新必须等待t+4的那个更新得到了之后才能计算平均的复合更新。所以使用的时候应该限制最长n步反馈的n,防止每次更新需要过长的等待时间。
![]() 算法可以被理解为一种特殊的平均n步更新的形式。这个平均包括了所有的n步更新,每一个的更新的系数都正比于
算法可以被理解为一种特殊的平均n步更新的形式。这个平均包括了所有的n步更新,每一个的更新的系数都正比于![]() ,而所有的系数之和为1;。得到的平均之后的反馈值叫做
,而所有的系数之和为1;。得到的平均之后的反馈值叫做![]() -return:
-return:
下图显示了每一步反馈值的系数:
对于episode形式的反馈,我们可以将前面的反馈同最后一步的反馈分开,即为:
这个形式使得在系数为1的时候更加清楚反馈就是MC形式的反馈。而对于系数为0的时候反馈即为一步TD的反馈。
练习12.1
练习12.2
![]()
现在准备定义一个基于![]() -return的学习算法:the offline
-return的学习算法:the offline ![]() -return algorithm。作为一个线下算法,在遍历episode的时候不会改变系数w的值,等到episode结尾,一整个序列的更新都根据之前的半梯度法来进行系数的更新:
-return algorithm。作为一个线下算法,在遍历episode的时候不会改变系数w的值,等到episode结尾,一整个序列的更新都根据之前的半梯度法来进行系数的更新:
这个![]() -return给我们提供了一种能够和n步自举相比较的从MC平稳过度到one-step TD算法的另一种方式。目前我们采用的方法叫做一个学习算法的理论视角或者叫做forward views。每次访问一个状态,都需要观察未来状态的反馈并且考虑将它们进行组合。每次更新完一个状态我们都会往后前进一步,然后再也不会关心前面的状态。
-return给我们提供了一种能够和n步自举相比较的从MC平稳过度到one-step TD算法的另一种方式。目前我们采用的方法叫做一个学习算法的理论视角或者叫做forward views。每次访问一个状态,都需要观察未来状态的反馈并且考虑将它们进行组合。每次更新完一个状态我们都会往后前进一步,然后再也不会关心前面的状态。
12.2 
![]() 是强化学习算法中最古老也是应用最广的算法之一。则是第一个展示使用了资格迹的更偏理论的forward view和更适合计算的backward view的关系的算法。这里我们展示这个算法对于offline
是强化学习算法中最古老也是应用最广的算法之一。则是第一个展示使用了资格迹的更偏理论的forward view和更适合计算的backward view的关系的算法。这里我们展示这个算法对于offline ![]() -return算法的近似。
-return算法的近似。
![]() 相对于offline
相对于offline ![]() -return算法有三大改进:第一,这个算法能够在每一个状态对于权重向量进行更新而不是等到一个episode结束之后一起更新。第二,计算过程是均匀分布的而不是集中在episode的最后。第三,能够应用于continuing形式的问题而不仅仅是episodic形式。这一节介绍一个半梯度带函数近似版本的
-return算法有三大改进:第一,这个算法能够在每一个状态对于权重向量进行更新而不是等到一个episode结束之后一起更新。第二,计算过程是均匀分布的而不是集中在episode的最后。第三,能够应用于continuing形式的问题而不仅仅是episodic形式。这一节介绍一个半梯度带函数近似版本的![]() 算法。
算法。
资格迹是个和权重向量一样长的向量的短时记忆,一般比一整个episode持续的时间要短。它能够帮助学习过程中对于权重的更新,而权重会决定值函数的估计值。在![]() 中资格迹在开始时初始化为0,而随着时间步骤不断增加,之后乘以系数
中资格迹在开始时初始化为0,而随着时间步骤不断增加,之后乘以系数![]() 来进行衰减:
来进行衰减:
资格迹能够跟踪那些对于最近的状态值有所贡献的权重向量的分量(考虑到线性逼近中对于值函数的梯度就是特征向量x,因此资格迹可以看做是过往输入的特征向量的加权和)。TD error为:
在![]() 算法中权重向量每一步的更新都正比于TD error和资格迹向量:
算法中权重向量每一步的更新都正比于TD error和资格迹向量:
![]() 算法是往回看的。每次我们观察当前的TD error然后将它往回分配到每一个先前的状态中。分配是根据先前的那个状态对于当前的资格迹的贡献度。可以看做是站在当前状态往回看,如上图。当
算法是往回看的。每次我们观察当前的TD error然后将它往回分配到每一个先前的状态中。分配是根据先前的那个状态对于当前的资格迹的贡献度。可以看做是站在当前状态往回看,如上图。当![]() 的时候算法变为一步半梯度TD更新。在这里,只有当前状态的前一个状态会被当前TD error改变。而对于更大的
的时候算法变为一步半梯度TD更新。在这里,只有当前状态的前一个状态会被当前TD error改变。而对于更大的![]() 来说,更多的过往状态会被改变,但是距离当前状态更远的状态就会被当前TD error改变的更少因为相对应的资格迹的部分更小。
来说,更多的过往状态会被改变,但是距离当前状态更远的状态就会被当前TD error改变的更少因为相对应的资格迹的部分更小。
当![]() 时算法可以看作是MC算法的一种更通用的实现方式而且更有实用性。有两个优点:一、这时MC也能用于discounted continuing形式的任务。二、能够实现为增量式和在线形式。
时算法可以看作是MC算法的一种更通用的实现方式而且更有实用性。有两个优点:一、这时MC也能用于discounted continuing形式的任务。二、能够实现为增量式和在线形式。
线性![]() 被证明当步长系数满足2.7的情况下能够在on-policy形势下收敛。对于discounted形式,收敛得上限为:
被证明当步长系数满足2.7的情况下能够在on-policy形势下收敛。对于discounted形式,收敛得上限为:
练习12.3
练习12.4
(2)式和(3)式相等,交换求和顺序即可(不过不会写嘻嘻)。
12.3 n-step Truncated  -return Methods
-return Methods
offline ![]() -return算法是一种很重要的理想算法,但是它的应用有限因为需要使用直到episode结束才能够进行计算的
-return算法是一种很重要的理想算法,但是它的应用有限因为需要使用直到episode结束才能够进行计算的![]() -return。而且在continuing形式的问题里,
-return。而且在continuing形式的问题里,![]() -return是无法得到的。但是对于很多步之后的反馈值起始依赖很小,因为权重系数在不断的下降。综合考虑可以定义一种truncated
-return是无法得到的。但是对于很多步之后的反馈值起始依赖很小,因为权重系数在不断的下降。综合考虑可以定义一种truncated ![]() -return,只返回从t步开始h步之后的反馈的加权和,即:
-return,只返回从t步开始h步之后的反馈的加权和,即:
truncated ![]() -return带来了一组类似于第七章n步自举的n步
-return带来了一组类似于第七章n步自举的n步 ![]() -return算法。其中系数的更新为:
-return算法。其中系数的更新为:
12.4 Redoing Updates: Online  -return Algorithm
-return Algorithm
在truncated TD(![]() )算法中选择n引入了一组矛盾。n应该足够大因此算法才能够足够接近的拟合offline
)算法中选择n引入了一组矛盾。n应该足够大因此算法才能够足够接近的拟合offline ![]() -return算法。但是n又需要足够小这样更新才能足够快的计算并且尽快影响当前动作。我们能够同时获得这两个优点,但是需要付出更多计算复杂度的代价。
-return算法。但是n又需要足够小这样更新才能足够快的计算并且尽快影响当前动作。我们能够同时获得这两个优点,但是需要付出更多计算复杂度的代价。
方法是,每一个时间步骤当产生了一个新的数据,就从头开始重新计算所有的更新目标。因为每次考虑了新的数据,因此新的更新目标会比前一次的更好。也就是说更新总是相当于一个n步truncated ![]() -return,但是只是每次都计算到当前的时间终点为止。不断的计算当前能够计算得到最优的
-return,但是只是每次都计算到当前的时间终点为止。不断的计算当前能够计算得到最优的![]() -return,然后把它用来作为更新目标来更新权重向量。
-return,然后把它用来作为更新目标来更新权重向量。
这个理论上的算法需要遍历一个episode的所有状态很多次,每次都产生了一个不同的权重向量序列。h表示当前时间t开始计算的视野长度,那么所有产生的权重向量为:
因此更新的公式总结为:
这个更新公式同权重向量![]() 一起定义了一个online
一起定义了一个online ![]() -return 算法。
-return 算法。
这个online ![]() -return算法是完全的在线行驶,在每个时间步骤t计算当前系数
-return算法是完全的在线行驶,在每个时间步骤t计算当前系数![]() 。最重要的缺点就是计算复杂度太高,每个时间步都需要将当前步骤之前每一个部分都遍历一次。online形式的算法比offline形式的更复杂,因为offline的算法每次遍历每个状态的时候只有到结束状态才会进行更新。但online形式算法的结果更好,不仅是在offline不进行更新的计算过程中比其效果好,在最终计算结束后的结果上也更好。
。最重要的缺点就是计算复杂度太高,每个时间步都需要将当前步骤之前每一个部分都遍历一次。online形式的算法比offline形式的更复杂,因为offline的算法每次遍历每个状态的时候只有到结束状态才会进行更新。但online形式算法的结果更好,不仅是在offline不进行更新的计算过程中比其效果好,在最终计算结束后的结果上也更好。
12.5 True Online TD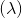
上一节介绍的online ![]() -return算法是目前表现最好的TD算法。这是一个使用online TD(
-return算法是目前表现最好的TD算法。这是一个使用online TD(![]() )只能近似的理想算法。目前展示的online
)只能近似的理想算法。目前展示的online ![]() -return算法还很复杂,可以将它从forward view转换为backward的形式得到一种能够高效计算的算法也就是true online TD(
-return算法还很复杂,可以将它从forward view转换为backward的形式得到一种能够高效计算的算法也就是true online TD(![]() )算法。这个算法叫做true online TD(
)算法。这个算法叫做true online TD(![]() )算法因为它比普通的TD(
)算法因为它比普通的TD(![]() )更接近理想的在线形式的
)更接近理想的在线形式的![]() -return算法。
-return算法。
推导太过复杂就不在这说。可以将online ![]() -return算法计算的权重向量列出来即:
-return算法计算的权重向量列出来即:
上面的三角形中的一列是一个时间步骤中算法计算得到的系数序列。我们实际上只需要每一行最后一个系数向量,因此新的策略就是找到一个直接有效的方式来根据上一行最后一个系数向量得到当前的系数向量。因此在线性情况下我们得出了一个true online TD(![]() )算法:
)算法:
算法已经被证明能够得出和online TD(![]() )算法完全一样的权重向量序列。但是这个算法需要的计算量更少。算法的空间需求是和传统的TD(
)算法完全一样的权重向量序列。但是这个算法需要的计算量更少。算法的空间需求是和传统的TD(![]() )算法一样,但是每一步的计算量增大了大概50%.因此每一步的计算复杂度依然是O(d)。
)算法一样,但是每一步的计算量增大了大概50%.因此每一步的计算复杂度依然是O(d)。
用在true online TD(![]() )算法中的资格迹叫做dutch trace,用来区分之前TD(
)算法中的资格迹叫做dutch trace,用来区分之前TD(![]() )算法中使用的accumulating trace。之前的研究中还有一个经常使用的资格迹叫做replacing trace,只用于表格形式的问题或者在像tile coding中产生的特征一样的二进制特征向量的问题。replacing trace是定义在特征向量的每一个分量上的,取决于其为0或者1:
)算法中使用的accumulating trace。之前的研究中还有一个经常使用的资格迹叫做replacing trace,只用于表格形式的问题或者在像tile coding中产生的特征一样的二进制特征向量的问题。replacing trace是定义在特征向量的每一个分量上的,取决于其为0或者1:
现在我们把replacing traces看作是dutch traces的粗糙逼近。dutch trace通常比replacing trace表现的更好而且有更清楚的理论解释。accumulating traces依然保留在那些无法使用dutch trace的非线性函数逼近的情形下。
12.6 Dutch Traces in Monte Carlo Learning
尽管资格迹紧密的和TD学习算法结合在一起,但实际上他们和TD并没有关系。实际上资格迹甚至可以直接用在MC算法中。之前展示了forward view的线性MC算法可以用来推导出一个等价而且计算更简单的backward-view形式的使用dutch traces的算法。这是本书中唯一显示说明forward-view 和 backward-view 等价的例子。
具体算法略过。
主要是说明资格迹和TD没关系。而且可以应用在任何的想要高效学习长期的函数估计的情形下。
12.7 Sarsa( )
)
只需要很小的变动就可以将这章前面讲的算法应用到带资格迹的动作值函数方法中。首先要改变n步反馈,将其中的v改为q:
这样我们就可以构造一个动作值函数形式的truncated ![]() -return。所以动作值函数形式的offline
-return。所以动作值函数形式的offline ![]() -return算法时需要用q替代v:
-return算法时需要用q替代v:
这个形式的backup diagrams和TD(![]() )的相同。
)的相同。
而动作值函数形式带资格迹的TD算法,叫做Sarsa(![]() )使用forward view的形式逼近上述形式的算法。它的更新形式和TD(
)使用forward view的形式逼近上述形式的算法。它的更新形式和TD(![]() )算法相同:
)算法相同:
线性函数近似形式的使用二进制特征的带accumulating trace或者replacing trace的Sarsa(![]() )算法伪代码如下:
)算法伪代码如下:
同样有一个动作值函数形式的理想状态的TD算法,也就是online ![]() -return算法。以及动作值函数形式的true online TD(
-return算法。以及动作值函数形式的true online TD(![]() )。只需要把对应的值函数改为q,状态特征值改为对应状态动作的形式即可。
)。只需要把对应的值函数改为q,状态特征值改为对应状态动作的形式即可。
最后还有一个truncated版本的Sarsa(![]() )算法,它在与多层ANN合用的时候能够作为一个高效的model-free的control算法。
)算法,它在与多层ANN合用的时候能够作为一个高效的model-free的control算法。
12.8 Variable  and
and 
快要接近对于基本的TD算法的介绍的结尾了。为了介绍最后一个通用形式的算法,先要把使用常数参数的自举和discounting泛化为使用依赖于状态和动作的形式。也就是每个时间步骤都有一个不同![]() 和
和![]() ,即
,即![]() 和
和![]() 。也就是让它们变成对于状态和动作的函数。
。也就是让它们变成对于状态和动作的函数。
介绍函数![]() ,termination function。这个函数改变了反馈的形式,而反馈是我们强化学习任务中需要估计的最重要的变量。于是现在我们把反馈表示为:
,termination function。这个函数改变了反馈的形式,而反馈是我们强化学习任务中需要估计的最重要的变量。于是现在我们把反馈表示为:
为了保证结果是有限值,需要保证 。这种形式的好处是episodic型的任务不需要在单独提出起始状态和结束状态。结束状态变成了一个
。这种形式的好处是episodic型的任务不需要在单独提出起始状态和结束状态。结束状态变成了一个![]() 并且转移到起始状态的状态。因此这种形式统一了episodic和discounted-continuing。
并且转移到起始状态的状态。因此这种形式统一了episodic和discounted-continuing。
对于自举的变量的泛化并不是像discounting一样是对于问题的改变,而是对于解决策略的改变。这个泛化影响了![]() -return。新的基于状态的
-return。新的基于状态的![]() -return可以写为:
-return可以写为:
这里每个![]() 都有一个状态s作为下标。这个等式表明
都有一个状态s作为下标。这个等式表明![]() -return可以有下一刻的奖励值加上第二项。第二项有可能为0,第二项里有两个部分,每部分的值有其自举的程度决定。 基于动作的
-return可以有下一刻的奖励值加上第二项。第二项有可能为0,第二项里有两个部分,每部分的值有其自举的程度决定。 基于动作的![]() -return可以写为Sarsa形式:
-return可以写为Sarsa形式:
或者expected Sarsa的形式:
其中
12.10 Watkins's Q( ) to Tree-Backup(
) to Tree-Backup( )
)
过去的一些年以及有不少将Q-learning与资格迹组合起来的算法。最初的像Watkins‘s Q(![]() )。这个算法只要是选择的是greedy动作就正常的衰退资格迹,否则就把第一个非greedy动作之后的资格迹置为0。第六章中我们将expected Sarsa和q-learning统一了起来。第七章中我们有介绍了n步 expected Sarsa和n步Tree Backup。现在展示一个资格迹版本的tree backup,叫做Tree-Backup(
)。这个算法只要是选择的是greedy动作就正常的衰退资格迹,否则就把第一个非greedy动作之后的资格迹置为0。第六章中我们将expected Sarsa和q-learning统一了起来。第七章中我们有介绍了n步 expected Sarsa和n步Tree Backup。现在展示一个资格迹版本的tree backup,叫做Tree-Backup(![]() )或者TB(
)或者TB(![]() )。这可以论证是Q-learning算法的继承者,因为保留了不需要使用Importance sampling的特性。
)。这可以论证是Q-learning算法的继承者,因为保留了不需要使用Importance sampling的特性。
TB(![]() )算法的思想是很直接的。就像是普通的TD(
)算法的思想是很直接的。就像是普通的TD(![]() ),这个算法就将每个长度的Treebackup组合起来。可以得到他们的递归形式:
),这个算法就将每个长度的Treebackup组合起来。可以得到他们的递归形式:
同样他也能够近似写为TD error的和的形式:
同样需要更新资格迹,不过增加了一个动作概率:
和w的更新一起定义了TB(![]() )的算法。就像所有的半梯度法一样,这个算法不保证在使用函数近似的off-policy情形下保持稳定。为了保持稳定,需要结合下一节的算法。
)的算法。就像所有的半梯度法一样,这个算法不保证在使用函数近似的off-policy情形下保持稳定。为了保持稳定,需要结合下一节的算法。
12.11 Stable Off-policy Methods with Traces
一些使用了资格迹在off-policy的情况下能够保证算法稳定。这里介绍四种在本书介绍的标准概念里最重要的四个算法,包括了通用形式的自举和discounting函数。所有的算法都使用了线性函数逼近,不过对于非线性函数逼近的拓展也可以在论文中找到。
这四个算法是:一,GTD(![]() ),是TDC算法的资格迹形式。TDC算法是双状态值的Gradient-TD算法的改进版。二,GQ算法,是Gradient-TD算法的带资格迹的动作值函数版本。三,HTD(
),是TDC算法的资格迹形式。TDC算法是双状态值的Gradient-TD算法的改进版。二,GQ算法,是Gradient-TD算法的带资格迹的动作值函数版本。三,HTD(![]() )算法是GTD(
)算法是GTD(![]() )和TD(
)和TD(![]() )算法的状态值函数形式的混合。四,Emphatic TD(
)算法的状态值函数形式的混合。四,Emphatic TD(![]() )算法,是一步Emphatic-TD算法到资格迹的延伸。
)算法,是一步Emphatic-TD算法到资格迹的延伸。
12.12 Implementation Issues
首先表格形式的算法看起来似乎比一步算法更难应用资格迹。简单的实现就需要在每个时间对每个状态更新它的值函数估计和资格迹。这对于传统的顺序计算计算机来说实现起来很有问题。还好参数![]() 和参数
和参数![]() 以及大部分状态的资格迹分量都接近0,只有那些拥有明显大于0的资格迹的状态需要被更新来逼近算法。
以及大部分状态的资格迹分量都接近0,只有那些拥有明显大于0的资格迹的状态需要被更新来逼近算法。
实际上在传统计算机上实现的算法可能只会跟踪那些有明显大于0的资格迹的状态。这样就能够在表格型算法中应用资格迹。当函数逼近方法使用了之后,不使用资格迹的计算优势就会变小。因此表格算法对于资格迹的计算复杂度来说是最坏的场景。
12.13 Conclusions
资格迹与TD error的结合提供了一个高效增量形式的在MC和TD算法之间转换和选择的方式。第七章介绍的n步算法也能做到,但是资格迹方法更加通用,学习速度更快而且共不同计算复杂度的选择。这一章主要介绍了优雅新兴的资格迹方法的理论解释。这个方法能够用于on-policy和off-policy,也能适应变化的自举和discounting。这个理论的一方面是true online方法,它能够精确复制计算量特别大的理论算法的结果,而且保留了传统TD算法计算的亲和力。另一方面是对于从更易理解的forward-view的方法到更容易计算的backward-view方法的转换推导。
第五章提到MC算法可以在非马尔科夫的任务中有优势,因为它不使用自举。因为资格迹方法使得TD算法更像MC算法,因此带资格迹的TD也能够得到这种优势。如果想用TD算法的一些特性而任务又是部分非马尔科夫的,就可以选择使用资格迹形式的TD。
通过调整![]() 我们可以将资格迹方法放置到MC到一步TD方法之间的任一个位置。对于应该把它放在哪还没有理论解释,但是经验告诉我们对于步骤比较长的任务使用资格迹比不使用效果更好。在两个方法中间的位置取得的效果一般比较好。虽然现在还不能够非常清楚地使用这个方法。
我们可以将资格迹方法放置到MC到一步TD方法之间的任一个位置。对于应该把它放在哪还没有理论解释,但是经验告诉我们对于步骤比较长的任务使用资格迹比不使用效果更好。在两个方法中间的位置取得的效果一般比较好。虽然现在还不能够非常清楚地使用这个方法。
使用资格迹方法需要比一步TD方法更多的计算量,但是它能够带来更快的学习速度。一般将资格迹用在数据比较稀疏而且不能重复的过程中,经常用在online的应用。而对于产生数据方便的时候经常不使用资格迹。
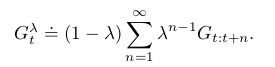








![\sum_{t=0}^{T-1}\alpha \delta_{t}z_{t} = \sum_{t=0}^{T-1}\alpha\delta_{t}\[\sum_{n=1}^{t}(\gamma\lambda)^{t-n}\bigtriangledown \widehat{v}(s_{n},w_{n})\] (2)](http://img.e-com-net.com/image/info8/65605726c7164cd2b24fd6b087e08dd5.gif)