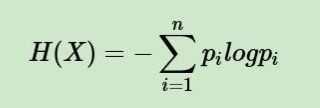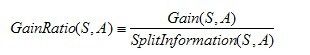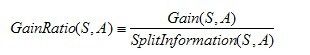实验室作业5.5-决策树

决策树

参考原文

参考原文

决策树算法在机器学习中算是很经典的一个算法系列了。它既可以作为分类算法，也可以作为回归算法，同时也特别适合集成学习比如随机森林。

分类与聚类

·Classification（分类），对于一个classifier，通常需要你告诉它“这个东西被分为某某类”这样一些例子，理想情况下，一个classifier会从它得到的训练集中进行“学习”，从而具备对未知数据进行分类的能力，这种提供训练数据的过程通常叫做supervised learning（监督学习）。

·而Clustering（聚类），简单的说是把相似的东西分到一组，聚类的时候，我们并不关心某一类是什么，我们需要实现的目标只是把相似的东西聚到一起，因此，一个聚类算法通常只需要知道如何计算相似度就可以开始工作了，因此clustering通常并不需要使用训练数据进行学习，这在Machine Learning中被称作unsupervised learning（无监督学习）。

常见的分类与聚类算法

分类，就是根据文本的特征和属性，划分到已有的类别中。如在自然语言处理NLP中，我们经常提到的文本分类便是一个分类问题，一般的模式分类方法都可用于文本分类研究。

常用的分类算法包括：决策树分类法，朴素的贝叶斯分类算法（native Bayesian classifier），基于支持向量机（SVM）的分类器，神经网络法，k-最近邻法（k-nearest neighbor kNN），模糊分类法等等。

分类作为一种监督学习方法，要求必须事先明确知道各个类别的信息，并且所有待分类项都有一个类别与之对应。但是很多时候上诉条件得不到满足，尤其是在处理海量数据的时候，如果通过预处理使得数据满足分类算法的要求，则代价非常大，这时候可以考虑使用聚类算法。

而K均值（K-means clustering）聚类则是最典型的聚类算法（当然，除此之外，还有很多诸如属于划分法K-MEDOIDS算法，CLARANS算法；属于层次法的BIRCH算法，CURE算法，CHAMELEON算法等；基于密度的方法：DBSCAN算法，OPTICS算法，DENCLUE算法等；基于网格的方法：STING算法，CLIQUE算法，WAVE-CLUSTER算法；基于模型的方法。）

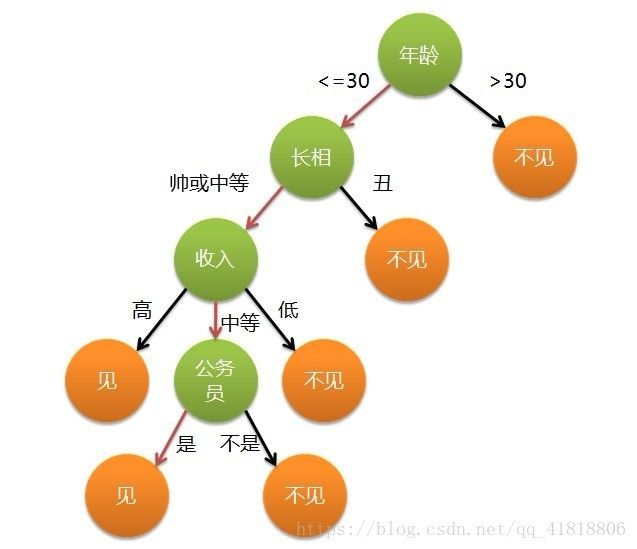
1.1.什么是决策树

    用于特征取值离散的情况，连续的特征一般也要处理成离散的。

    依托于策略抉择而建立

    机器学习中，决策树是一个预测模型；它代表的是对象属性与对象值之间的一中 映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的是某个可能的属性值，而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。

    从数据产生决策树的机器学习技术叫做决策树学习，通俗点说就是决策树，说白了，这是一种依托于分类、训练上的预测树，根据已知预测、归类未来。

例子

一

    一个女孩子相亲的过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑：

    也就是说，决策树的简单策略就是，好比公司招聘面试过程中筛选一个人的简历，如果你的条件相当好比如说某985/211重点大学博士毕业，那么二话不说，直接叫过来面试，如果非重点大学毕业，但实际项目经验丰富，那么也要考虑过来面试一下，即所谓具体情况具体分析、决策。但每一个未知的选项都是可以归类到已有的分类类别中的。

二

 此例子来自Tom M.Mitchell著的机器学习一书：

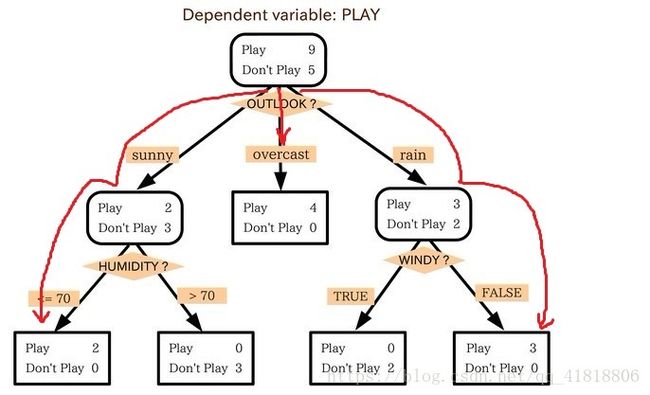
    小王的目的是通过下周天气预报寻找什么时候人们会打高尔夫，他了解到人们决定是否打球的原因最主要取决于天气情况。而天气状况有晴，云和雨；气温用华氏温度表示；相对湿度用百分比；还有有无风。如此，我们便可以构造一棵决策树，如下（根据天气这个分类决策这天是否合适打网球）：

上述决策树对应于以下表达式：

（Outlook=Sunny ^Humidity<=70）V （Outlook = Overcast）V （Outlook=Rain ^ Wind=Weak）

ID3算法的信息论基础

机器学习算法其实很古老，当我们敲if，else，if，else，其实就已经在用到决策树的思想了。那么多条件的情况下，用哪个特征先做if，哪个条件特征后作if比较优呢？怎么准确地定量选择这个标准就是决策树机器学习算法的关键了。

信息增益的度量标准：熵

    ID3算法的核心思想就是“以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂”。而信息增益的度量标准是熵。

    ID3算法的核心问题是选取在树的每个结点要测试的属性。我们希望选择的是最有利于分类实例的属性，信息增益（Information Gain）是用来衡量给定的属性区分训练样例的能力，ID3算法在增长树的每一步使用信息增益从候选属性中选择属性。

    为了精确的定义信息增益，我们先定义信息论中广泛使用的一个度量标准，称为熵（entropy），它刻画了任意样例的纯度（purity）。给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：

上述公式中，p+代表正样例，而p-代表反样例。（在有关熵的所有计算中我们定义0log0为0）

举例来说，假设S是一个关于布尔概念的有14个样例的集合，它包括9个正例和5个反例（我们采用[9+,5-]来概括这样的数据样例），那么S相对于这个布尔样例的熵为：

Entropy（[9+,5-]）=-(9/14)log2(9/14)-(5/14)log2(5/14)=0.940

根据上诉这个公式，我们可以得到：S的所有成员属于同一类，Entropy（S）=0；S的正反例数量相等，Entrpy（S）=1；S的正反例数量不等，熵介于0，1之间。如下图所示：

熵度量了事物的不确定性，越不确定的事物，它的熵就越大。

信息熵公式：

其中n代表X的n种不同的离散取值，而pi代表了X取值为i的概率，log为以2或者e为底的对数。举个例子，比如X有两个可能的取值，而这两个取值各为1/2时X的熵最大，此时X具有最大的不确定性，值为H(X)=-(1/2log1/2+1/2log1/2)=log2。如果两个值概率发生变化，则不确定性减少，对应的熵也会减少。比如一个

概率1/3，另一个2/3，则对应的熵为H(X)=-(1/3log1/3+2/3log2/3)=log3-2/3log2

多个变量的联合熵

条件熵

类似于条件概率，它度量了我们的X在知道Y以后剩下的不确定性

H(X)度量了X的不确定性，条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性，那么H(X)-H(X|Y)度量了X在知道Y以后不确定性减少程度。这个度量信息我们在信息论中称为互信息，记为I(X,Y)。在决策树ID3算法中叫信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大，则越适合用来分类。

2、信息增益度量期望的熵降低

信息增益Gain（S，A）定义

信息增益（information gain）是属性分类训练数据的效力的度量标准。简单的说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低（或者说，样本按照某属性划分时造成熵减少的期望）。更精确的讲，一个属性A相对样例集合S的信息增益Gain（S，A）被定义为：

 其中 Values(A)是属性A所有可能值的集合，是S中属性A的值为v的子集。换句话来讲，Gain(S,A)是由于给定属性A的值而得到的关于目标函数值的信息。当对S的一个任意成员的目标值编码时，Gain(S,A)的值是在知道属性A的值后可以节省的二进制位数。

下面，举个例子，假定S是一套有关天气的训练样例，描述它的属性包括可能是具有Weak和Strong两个值的Wind。像前面一样，假定S包含14个样例，[9+，5-]。在这14个样例中，假定正例中的6个和反例中的2个有Wind =Weak，其他的有Wind=Strong。由于按照属性Wind分类14个样例得到的信息增益可以计算如下。

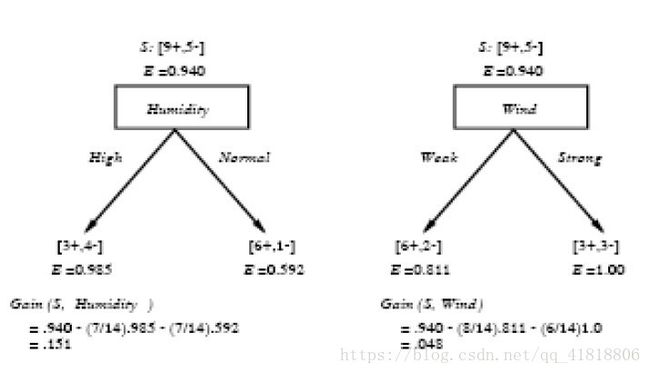
运用在本文开头举得第二个根据天气情况是否决定打羽毛球的例子上，得到的最佳分类属性如下图所示：

在上图中，计算了两个不同属性：湿度(humidity)和风力(wind)的信息增益，最终humidity这种分类的信息增益0.151>wind增益的0.048。说白了，就是在星期六上午是否适合打网球的问题诀策中，采取humidity较wind作为分类属性更佳，决策树由此而来。

1.2.ID3算法

1.2.1.

    ID3算法是决策树算法的一种。在了解什么是ID3算法之前，我们得先明白一个概念：奥卡姆剃刀。

    · 奥卡姆剃刀（Occam's Razor,Ockham's Razor），又称“奥坎的剃刀”，是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉（William of Occam,约1285年至1349年）提出，他在《箴言书注》 2卷15题说“切勿浪费较多的东西，去做‘用较少的东西，同样可以做好的事情’。”简单点说，便是：be simple.

    ID3算法（Iterative Dichotomiser 3 迭代二叉树3代）是一个由Ross Quinlan发明的用于决策树的算法。这个算法就是建立在上诉所介绍的奥卡姆剃刀的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。尽管如此，该算法也不是总是生成最小的树形结构，而是一个启发式算法。

   从信息论中我们知道，期望信息越小，信息增益越大，从而纯度越高。ID3算法的核心思想就是以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。

     所以，ID3的思想便是：

    1.自顶向下的贪婪搜索遍历可能的决策树空间构造决策树（此方法是ID3算法和C4.5算法的基础）；

     2.从“哪一个属性将在树的根节点被测试”开始；

     3.  使用统计测试来确定每一个实例属性单独分类训练样例的能力，分类能力最好的属性作为树的根节点测试（评判一个属性的分类能力用信息增益or信息增益率）；

    4.然后为根节点属性的每个可能值产生一个分支，并把训练样例排列到适当的分支（也就是说，样例的该属性值对应的分支）之下；

    5.重复这个过程，用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。

这形成了对合格决策树的贪婪搜索，也就是算法从不回溯重新考虑以前的选择。

    下图所示即是用于学习布尔函数的ID3算法概要：

1.2.3、ID3算法决策树的形成

    下图为ID3算法第一步后形成的部分决策树。这样综合起来看，就容易理解多了。1、overcast样例必为正，所以为叶子结点，总为yes；2、ID3无回溯，局部最优，而非全局最优，还有另一种树后修剪决策树。下图是ID3算法第一步后形成的部分决策树：

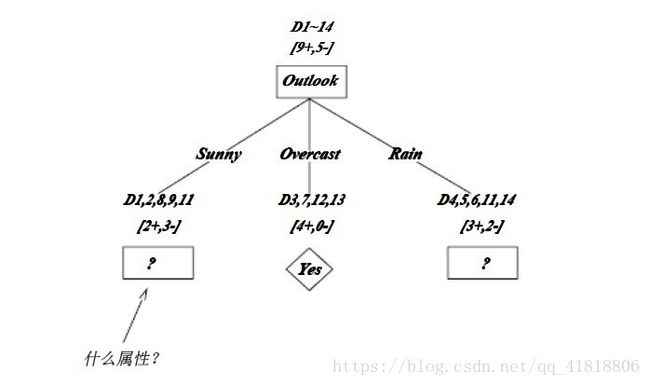
  如上图，训练样例被排列到对应的分支结点。分支Overcast的所有样例都是正例，所以成为目标分类为Yes的叶结点。另两个结点将被进一步展开，方法是按照新的样例子集选取信息增益最高的属性。

1.3、C4.5算法

1.3.1、ID3算法的改进：C4.5算法

    C4.5，是机器学习算法中的另一个分类决策树算法，它是决策树的核心算法。

    决策树构造方法其实就是每次选择一个好的特征以及分裂点作为当前节点的分类条件。

    C4.5算法相对于ID3改进的地方：

      1.  用信息增益率来选择属性。ID3选择属性用的是子树的信息增益，这里可以用很多方法来定义信息，ID3使用的是熵(entropy，熵是一种不纯度度量准则),也就是熵的变化值，而C4.5用的是信息增益率。对，区别就在于一个是信息增益，一个是信息增益率。

        2.在树构造过程中进行剪枝，在构造决策树的时候，那些挂着几个元素的节点，不考虑最好，不然容易导致overfitting。

        3.对非离散数据也能处理。

        4.能够对不完整数据进行处理。

     针对上述第一点，解释下：一般来说率就是用来取平衡用的，就像方差起的作用差不多，比如有两个跑步的人，一个起点是10m/s的人、其10s后为20m/s；另一个人起速是1m/s、其1s后为2m/s。如果紧紧算差值那么两个差距就很大了，如果使用速度增加率(加速度，即都是为1m/s^2)来衡量，2个人就是一样的加速度。因此，C4.5克服了ID3用信息增益选择属性时偏向选择取值多的属性的不足。

C4.5算法之信息增益率

定义：

增益比率度量，是用前面的增益度量Gain(S，A)和分裂信息度量SplitInformation(S，A)来共同定义的，如下所示：

分裂信息用来衡量属性分裂数据的广度和均匀，其定义为：

     其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。分裂信息实际上就是S关于属性A的各值的熵。这与我们前面对熵的使用不同，在那里我们只考虑S关于学习到的树要预测的目标属性的值的熵。

    分裂信息项阻碍选择值为均匀分布的属性。例如，考虑一个含有n个样例的集合被属性A彻底分割（译注：分成n组，即一个样例一组）。这时分裂信息的值为log2n。相反，一个布尔属性B分割同样的n个实例，如果恰好平分两半，那么分裂信息是1。如果属性A和B产生同样的信息增益，那么根据增益比率度量，明显B会得分更高。

    使用增益比率代替增益来选择属性产生的一个实际问题是，当某个Si接近S（|Si|»|S|）时分母可能为0或非常小。如果某个属性对于S的所有样例有几乎同样的值，这时要么导致增益比率未定义，要么是增益比率非常大。为了避免选择这种属性，我们可以采用这样一些启发式规则，比如先计算每个属性的增益，然后仅对那些增益高过平均值的属性应用增益比率测试（Quinlan 1986）。

    除了信息增益，Lopez de Mantaras（1991）介绍了另一种直接针对上述问题而设计的度量，它是基于距离的（distance-based）。这个度量标准基于所定义的一个数据划分间的距离尺度。具体更多请参看：Tom M.Mitchhell所著的机器学习之3.7.3节。

1.3.3、C4.5算法实现中的几个关键步骤

决策树学习C4.5算法中4个重要概念的表达，如下：

1.

2.

3.

4.

总结：

1.实际应用中，决策树overfitting比较严重，一般要做boosting。分类器的性能上不去，很主要的原因在于特征的鉴别性不足，而不是分类器的好坏，好的特征才有好的分类效果，分类器只是弱相关。

2.那如何提高 特征的鉴别性呢？一是设计特征时尽量引入domain knowledge，二是对提取出来的特征做选择、变换和再学习，这一点是机器学习算法不管的部分(不针对决策树，因此不能说是决策树的特点，只是一些机器学习算法在应用过程中的经验体会)。