Datawhale_温习概率统计(3)——常见分布与假设检验

一、二项分布，泊松分布，正态分布的关系

1.1 二项分布（Binomial distribution）

二项分布可以认为是一种只有两种结果（成功/失败)的单次试验重复多次后成功次数的分布概率。
二项分布需要满足以下条件：

• 试验次数是固定的
• 每次试验都是独立的
• 对于每次试验成功的概率都是一样的

一些二项分布的例子：

• 销售电话成功的次数
• 一批产品中有缺陷的产品数量
• 掷硬币正面朝上的次数
• 在一袋糖果中取糖果吃，拿到红色包装的次数

在n次试验中，单次试验成功率为p，失败率q=1-p，则出现成功次数的概率为
$$P(X=x)=C_n^x{p}^x{q}^{n-x}$$

1.2 泊松分布（Poisson distribution）

泊松分布是用来描述泊松试验的一种分布，满足以下两个特征的试验可以认为是泊松试验：

• 所考察的事件在任意两个长度相等的区间里发生一次的机会均等
• 所考察的事件在任何一个区间里发生与否和在其他区间里发生与否没有相互影响，即是独立的

泊松分布需要满足一些条件：

• 试验次数n趋向于无穷大
• 单次事件发生的概率p趋向于0
• np是一个有限的数值

泊松分布的一些例子：

• 一定时间段内，某航空公司接到的订票电话数
• 一定时间内，到车站等候公交汽车的人数
• 一匹布上发现的瑕疵点的个数
• 一定页数的书刊上出现的错别字个数

一个服从泊松分布的随机变量X，在具有比率参数（rate parameter）λ （λ=np）的一段固定时间间隔内，事件发生次数为i的概率为
$$P\{X=i\}=e^{-\lambda }\frac{{\lambda }^i}{i!}$$

1.3 正态分布（Normal distribution）

正态分布，也叫做高斯分布，是最为常见的统计分布之一，是一种对称的分布，概率密度呈现钟摆的形状，其概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(x-u{)}^2}{2{\sigma }^2}}$$
记为X ~ N(μ, ${\sigma }^2$) , 其中μ为正态分布的均值，σ为正态分布的标准差

有了一般正态分布后，可以通过公式变换将其转变为标准正态分布 Z ~ N(0,1)，
$$Z=\frac{X-\mu }{\sigma }$$
正态分布的一些例子：

• 成人的身高
• 不同方向的气体分子的运动速度
• 测量物体质量时的误差

1.4 三者的关系

正态分布在现实生活有着非常多的例子，这一点可以从中心极限定理来解释，中心极限定理说的是一组独立同分布的随机样本的平均值近似为正态分布，无论随机变量的总体符合何种分布

当n很大，p很小时，如n ≥ 100 and np ≤ 10时，二项分布可以近似为泊松分布。

当λ很大时，如λ≥1000时，泊松分布可以近似为正态分布。

当n很大时，np和n(1-p)都足够大时，如n ≥ 100 , np ≥10，n(1-p) ≥10时，二项分布可以近似为正态分布。

二、python&numpy简单实现

2.1 简单实现

import matplotlib.pyplot as plt
import numpy as np 
def n_1(n):
    if n <= 1:
        return 1.0
    return n * n_1(n-1)

def A_mn(m, n):
    return n_1(n) / n_1(n - m)

def C_mn(m, n):
    # A_mn/n_1(m)
    return n_1(n) / (n_1(m) * n_1(n - m))


def binorma(m, n, p):
    # 二项分布
    return C_mn(m, n) * p**m *(1.0 -p)**(n-m) 


def poisson(x, l):
    # 泊松分布
    out = (np.e ** -l) * (l ** x) / n_1(x)
    return out 

def normal_ds(x, mean_ = 0, std_ = 1):
    return 1 / np.sqrt(2 * std_ * np.pi) * np.exp(-1*(x - mean_)**2 / (2 * std_**2))

2.2 分布间关系

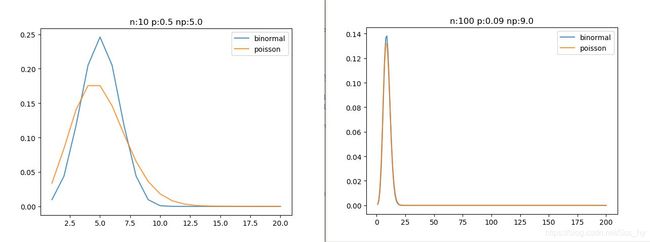
• 当n 很大， p很小时， n >= 100 and np <= 10 二项分布接近泊松分布

def plot_pos_bin(n, p):
    a, b = [], []
    l = n * p
    x = list(range(1, n*2+1))
    for i in x:
        try:
            # 返回的是概率密度
            tmp = binorma(i, n, p)
            tmp1 = poisson(i, l)
            a.append(tmp)
            b.append(tmp1)
        except:
            print(f'{i} 超出计算范围')

    plt.plot(x[:len(a)], a, label="binormal", alpha=0.8)
    plt.plot(x[:len(b)], b, label="poisson", alpha=0.8)
    plt.legend()
    plt.title(f'n:{n} p:{p} np:{n*p}')
    plt.show()

plot_pos_bin(10, 0.5)
plot_pos_bin(100, 0.09)

• numpy

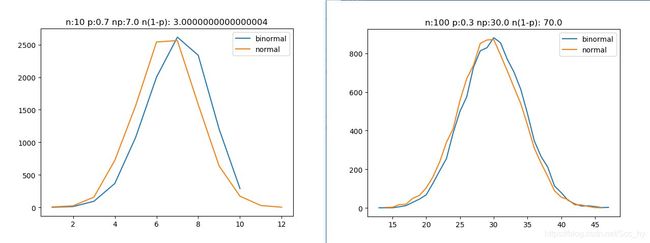
# np和(1-p) 都足够大时， 如果 n>=100 np >=10 n(1-p)>=10 二项分布可以近似为正态分布
import numpy as np 
def plot_bin_norm(n = 100, p = 0.3):
    binormal_lst = np.random.binomial(n=n, p=p,size=10000)
    unq_, cnt = np.unique(binormal_lst, return_counts=True)

    normal_lst = np.random.normal(n * p, np.sqrt(n * p * (1-p)), size = 10000)
    normal_lst = normal_lst.astype(int)
    unq_n, cnt_n = np.unique(normal_lst, return_counts=True)

    plt.plot(unq_, cnt, label='binormal')
    plt.plot(unq_n, cnt_n, label = 'normal')
    plt.title(f'n:{n} p:{p} np:{n*p} n(1-p): {n*(1-p)}')
    plt.legend()
    plt.show()

plot_bin_norm(100, 0.3)
plot_bin_norm(10, 0.7)

三、pmf与cdf的生成

3.1 概率质量分布pmf

import scipy.stats as sts 

# 计算二项分布B(10,0.5)的PMF
x = list(range(11))
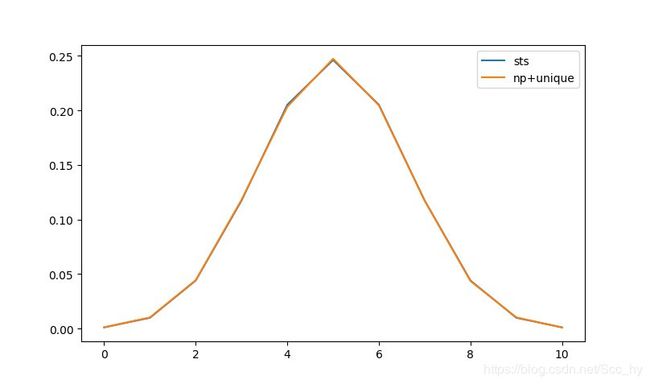
p = sts.binom.pmf(x, n=10, p=0.5)
# 本质上应该是和下列操作一致的：
bin_lst = np.random.binomial(n=10, p=0.5, size=100000)
bin_uniq, bin_cnt = np.unique(bin_lst, return_counts=True)
p_ = bin_cnt / bin_cnt.sum()
plt.plot(x, p, label='sts')
plt.plot(x, p_, label='np+unique')
plt.legend()
plt.show()


# 计算泊松分布P(1)的PMF
x=range(11)
p=sts.poisson.pmf(x, mu=1)

# 计算均匀分布U(0,1)的PDF
x = numpy.linspace(0,1,100)
p= sts.uniform.pdf(x,loc=0, scale=1)

# 计算正态分布N(0,1)的PDF
x = numpy.linspace(-3,3,1000)
p= sts.norm.pdf(x,loc=0, scale=1)

3.2 概率密度分布pmf

x = list(range(11))
p_cdf = sts.binom.cdf(x, n=10, p=0.5)
# 本质上应该是和下列操作一致的：
bin_lst = np.random.binomial(n=10, p=0.5, size=100000)
bin_uniq, bin_cnt = np.unique(bin_lst, return_counts=True)
p_ = bin_cnt / bin_cnt.sum()
p_cdf_ = np.cumsum(p_)

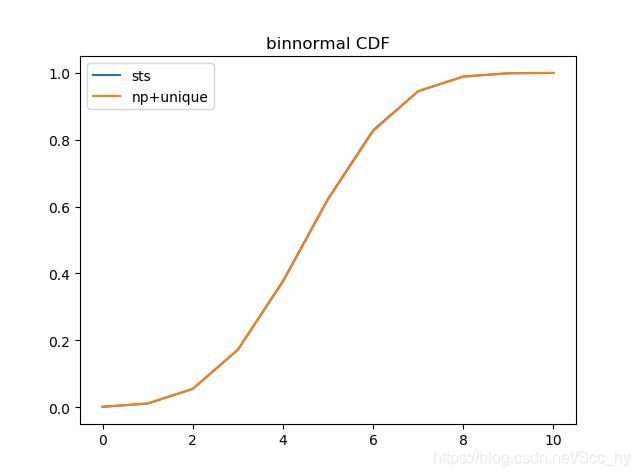
plt.plot(x, p_cdf, label='sts')
plt.plot(x, p_cdf_, label='np+unique')
plt.legend()
plt.title('binnormal CDF')
plt.show()

四、假设检验

4.1 基本概念

假设检验问题时统计推断中的一类重要问题，在总体的分布函数完全未知或只知其形式，不知其参数的情况，为了推断总体的某些未知特性，提出某些关于总体的假设，这类问题被称为假设检验。

4.2 基本步骤

一个假设检验问题可以分为5步，无论细节如果变化，都一定会遵循这5个步骤。

1. 陈述研究假设，包含原假设（null hypothesis）和备择假设（alternate hypothesis）
2. 为验证假设收集数据
3. 构造合适的统计测试量并测试
4. 决定是接受还是拒绝原假设
5. 展示结论

步骤1：

通常来说，我们会把原假设的描述写成变量之间不存在某种差异，或不存在某种关联，备择假设则为存在某种差异或关联。
例如，原假设：男人和女人的平均身高没有差别， 备择假设男人和女人的平均身高存在显著差别。

步骤2:

为了统计检验的结果真实可靠，需要根据实际的假设命题从总体中抽取样本，要求抽样的数据要具有代表性，例如在上述男女平均身高的命题中，抽取的样本要能覆盖到各类社会阶级，各个国家等所有可能影响到身高的因素。

步骤3：

统计检验量有很多种类，但是所有的统计检验都是基于组内方差和组间方差的比较，如果组间方差足够大，使得不同组之间几乎没有重叠，那么统计量会反映出一个非常小的P值，意味着不同组之间的差异不可能是由偶然性导致的。

步骤4：

基于统计量的结果做出接受或拒绝原假设的判断，通常我们会以P=0.05作为临界值（单侧检验）。

步骤5：

展示结论。

4.3 统计量的选择

选择合适的统计量是进行假设检验的关键步骤，最常用的统计检验包括回归检验(regression test)，比较检验(comparison test)和关联检验(correlation test)三类。

回归检验

回归检验适用于预测变量是数值型的情况，根据预测变量的数量和结果变量的类型又分为以下几种。

	预测变量	结果变量
简单线性回归	单个，连续数值	连续数值
多重线性回归	多个，连续数值	连续数值
Logistic回归	连续数值	二元类别

比较检验

比较检验适用于预测变量是类别型，结果变量是数值型的情况，根据预测变量的分组数量和结果变量的数量又可以分为以下几种。

	预测变量	结果变量
Paired t-test	两组，类别	组来自同一总体，数值
Independent t-test	两组，类别	组来自不同总体，数值
ANOVA	两组及以上，类别	单个，数值
MANOVA	两组及以上，类别	两个及以上，数值

关联检验

关联检验常用的只有卡方检验一种，适用于预测变量和结果变量均为类别型的情况。

非参数检验

此外，由于一般来说上述参数检验都需满足一些前提条件，样本之间独立，不同组的组内方差近似和数据满足正态性，所以当这些条件不满足的时候，我们可以尝试用非参数检验来代替参数检验。

非参数检验	用于替代的参数检验
Spearman	回归和关联检验
Sign test	T-test
Kruskal–Wallis	ANOVA
ANOSIM	MANOVA
Wilcoxon Rank-Sum test	Independent t-test
Wilcoxon Signed-rank test	Paired t-test

4.4 两类错误

事实上当我们进行假设检验的过程中是存在犯错误的可能的，并且理论上来说错误是无法完全避免的。根据定义，错误分为两类，一类错误（type I error）和二类错误（type II error）。

• 一类错误：拒绝真的原假设

• 二类错误：接受错误的原假设

一类错误可以通过α值来控制，在假设检验中选择的 α（显著性水平）对一类错误有着直接影响。α可以认为是我们犯一类错误的最大可能性。以95%的置信水平为例，a=0.05，这意味着我们拒绝一个真的原假设的可能性是5%。从长期来看，每做20次假设检验会有一次犯一类错误的事件发生。

二类错误通常是由小样本或高样本方差导致的，二类错误的概率可以用β来表示，和一类错误不同的是，此类错误是不能通过设置一个错误率来直接控制的。对于二类错误，可以从功效的角度来估计，首先进行功效分析（power analysis）计算出功效值1-β，进而得到二类错误的估计值β。

一般来说这两类错误是无法同时降低的，在降低犯一类错误的前提下会增加犯二类错误的可能性，在实际案例中如何平衡这两类错误取决于我们更能接受一类错误还是二类错误。

4.5 假设检验Python实现

4.5.1 正态检验

Shapiro-Wilk Test是一种经典的正态检验方法。

H0: 样本总体服从正态分布
H1: 样本总体不服从正态分布

import numpy as np
from scipy.stats import shapiro
data_nonnormal = np.random.exponential(size=100) # 指数分布
data_normal = np.random.normal(size=100) # 正态分布

def normal_judge(data):
	stat, p = shapiro(data)
	if p > 0.05:
		return 'stat={:.3f}, p = {:.3f}, probably gaussian'.format(stat,p)
	else:
		return 'stat={:.3f}, p = {:.3f}, probably not gaussian'.format(stat,p)

# output
normal_judge(data_nonnormal)
# 'stat=0.850, p = 0.000, probably not gaussian'
normal_judge(data_normal)
# 'stat=0.987, p = 0.415, probably gaussian'

4.5.2 卡方检验

目的：检验两组类别变量是相关的还是独立的

H0: 两个样本是独立的
H1: 两组样本不是独立的

from scipy.stats import chi2_contingency
table = [[10, 20, 30],[6,  9,  17]]
stat, p, dof, expected = chi2_contingency(table)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
	print('Probably independent')
else:
	print('Probably dependent')

 # output
#stat=0.272, p=0.873
#Probably independent

4.5.3 T-test

目的：检验两个独立样本集的均值是否具有显著差异
H0: 均值是相等的
H1: 均值是不等的

from scipy.stats import ttest_ind
import numpy as np
data1 = np.random.normal(size=10)
data2 = np.random.normal(size=10)
stat, p = ttest_ind(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
	print('Probably the same distribution')
else:
	print('Probably different distributions')
    
# output
# stat=-1.382, p=0.184
# Probably the same distribution

4.5.4 ANOVA

目的：与t-test类似，ANOVA可以检验两组及以上独立样本集的均值是否具有显著差异

H0: 均值是相等的
H1: 均值是不等的

from scipy.stats import f_oneway
import numpy as np
data1 = np.random.normal(size=10)
data2 = np.random.normal(size=10)
data3 = np.random.normal(size=10)
stat, p = f_oneway(data1, data2, data3)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
	print('Probably the same distribution')
else:
	print('Probably different distributions')
 
# output
# stat=0.189, p=0.829
# Probably the same distribution

4.5.5 Mann-Whitney U Test

目的：检验两个样本集的分布是否相同

H0: 两个样本集的分布相同
H1: 两个样本集的分布不同

from scipy.stats import mannwhitneyu
data1 = [0.873, 2.817, 0.121, -0.945, -0.055, -1.436, 0.360, -1.478, -1.637, -1.869]
data2 = [1.142, -0.432, -0.938, -0.729, -0.846, -0.157, 0.500, 1.183, -1.075, -0.169]
stat, p = mannwhitneyu(data1, data2)
print('stat=%.3f, p=%.3f' % (stat, p))
if p > 0.05:
	print('Probably the same distribution')
else:
	print('Probably different distributions')

# output
# stat=40.000, p=0.236
# Probably the same distribution