算法之动态规划法(java)最长递减子序列,最长公共子序列,0-1背包问题
算法之动态规划法(java)最长递减子序列,最长公共子序列,0-1背包问题
1.概念:
- 动态规划(Dynamic programming)是运筹学的一个分支,是求解决策过程最优化的数学方法。
- 动态规划处理的对象是多阶段决策问题。
- 多阶段决策问题: 问题可以分解成若干相互联系的阶段,在每一个阶段都要做出决策,形成一个决策序列。最终获取最优决策序列(最优策略),即得到最优解。
2.动态规划设计思想
3.最长递减子序列问题
案例提出:
给定由n个整数a1,a2,…,an构成的序列,在这个序列中随意删除一些元素后可得到一个子序列ai,aj,ak,…,am,其中1≤i≤m≤n,i
1> 第一步就是划分子问题。
假设序列a[i],a[m],…,a[n],a[k],a[j]是以a[j]为尾元素的最长递减子序列,它的长度值为b[j],且a[i]>a[m]>…>a[n]>a[k]>a[j]。必然有下面这个结论成立,那就是a[i],a[m],…,a[n],a[k]一定是以a[k]为尾元素的最长递减子序列,它的长度值为b[k],且a[i]>a[m]>…>a[n]>a[k]。
b[j]和b[k]存在关系: b[j]=b[k]+1。
2> 第二步就是建立子问题的递推关系。
要求以元素a[j]为尾元素的最长递减子序列的长度b[j],只需穷举出a[j]之前所有比a[j]大的元素a[k],满足k
b[j]=max{ b[k]+1 | k
3> 第三步就是以自底向上的方式计算各个b[j]
先求b[1],显然b[1]就等于1,求完b[1]后,根据a[1]与a[2]的大小关系来更新b[2],求完b[2]后,根据a[1]、a[2]与a[3]的大小关系来更新b[3]……,依此类推,直至求到b[n]时,根据前n-1个数与a[n]的大小关系来更新b[n],求完b[n]后,n个b[j]中的最大者就是整个数组的最长递减子序列的长度。
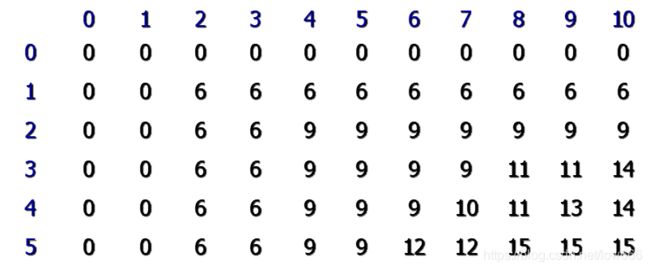
例:给定一个含有6个元素的数组a,下表给出了数组b的各个元素的值。

答案: 显然b[6]最大,为4,因此数组a的最长递减子序列长度为4。
代码:
package com.sun.main;
import java.util.ArrayList;
public class MaxList {
public static void main(String[] args) {
int[] num = {65, 22, 34, 99, 27, 25, 100, 33, 35, 200, 44, 57};
list(num);
}
private static void list(int[] num) {
if (num == null) {
return;
}
int max = 0;
ArrayList<Integer> arrayList = new ArrayList<Integer>();
for (int i = 0; i < num.length; i++) {
if (max == 0) {
arrayList.add(num[i]);
max ++;
continue;
}
if (arrayList.get(max - 1) < num[i]) {
arrayList.add(num[i]);
max ++;
} else {
// 找到比它大,但是最小的那个数据,替换掉
int left = binarySearch(arrayList, max, num[i]);
arrayList.set(left, num[i]);
}
}
System.out.println("最大递增长度为:" + max);
}
private static int binarySearch(ArrayList<Integer> arrayList, int right, int n) {
int left = 0;
while (left < right){
int mid = (right + left) / 2;
if (arrayList.get(mid) >= n) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
结果:
4.最长公共子序列
案例提出:
X 的子序列 Z :设序列 X, Z,

若存在 X 的元素构成的下标严格递增序列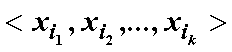
使得 ,则称 Z 是 X 的子序列。
X 与 Y 的公共子序列 Z :Z 是 X 和 Y 的子序列。
给定序列 X=
例: X: A B C B D A B
Y: B D C A B A
一个最长公共子序列: B C B A
分析:
1> 第一步就是划分子问题。
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
(1)若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。
(2)若xm≠yn且zk≠xm,则Z是xm-1和Y的最长公共子序列。
(3)若xm≠yn且zk≠yn,则Z是X和yn-1的最长公共子序列。
2> 第二步就是建立子问题的递推关系。
用c[i][j]记录序列Xi={x1,x2,…,xi}和Yj={y1,y2,…,yj}的最长公共子序列的长度。递推归关系如下:

3> 第三步就是以自底向上的方式计算。
当序列X为空时,考察当序列Y为空时,Y有一个元素,Y有两个元素时,一直到Y有n个元素时两者的最长公共子序列。
当X有一个元素时,考察当Y为空时,Y有一个元素,Y有两个元素时,一直到Y有n个元素时两者的最长公共子序列。
当X有两个元素时,做同样的计算。
当X有m个元素时,考察当Y为空时,Y有一个元素,Y有两个元素时,一直到Y有n个元素时两者的最长公共子序列。这时就求出的问题的最优值了。
代码:
package com.sun.main;
public class MaxPublic {
public static void main(String[] args) {
String str1 = "ABCBDAB";
String str2 = "BDCABA";
maxPublic(str1, str2);
}
public static void maxPublic(String str1, String str2) {
int str1Len = str1.length();
int str2Len = str2.length();
int[][] cLenNUm = new int[str1.length() + 1][str2.length() + 1];//默认赋值,[0][?],[?][0]默认两侧皆0,类似公式中0的场景
//构造一个长度数组
for (int i = 1; i <= str1Len; i++) {
for (int j = 1; j <= str2Len; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {//对应公式第二条相等
cLenNUm[i][j] = cLenNUm[i - 1][j - 1] + 1;
} else {//对应公式第三条不相等
cLenNUm[i][j] = Math.max(cLenNUm[i][j - 1], cLenNUm[i - 1][j]);
}
}
}
//反推结果
int i = str1Len;
int j = str2Len;
StringBuffer sb = new StringBuffer();//作为结果
while (i > 0 && j > 0) {//这里其实处理了i=0,j=0的,对应公式0的反推场景
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {//反推公式中不相等的场景
//该值一定是被选取到的,根据之前的公式,知道两条字符串的下标都前进一位
sb.append(str1.charAt(i - 1));
i--;
j--;
} else {//对应公式中不相等的反推场景
if (cLenNUm[i][j - 1] > cLenNUm[i - 1][j]) {//找大的那个方向,此处是左边大于上面,则该处的结果是来自左边
j--;
} else if (cLenNUm[i][j - 1] < cLenNUm[i - 1][j]) {
i--;
} else if (cLenNUm[i][j - 1] == cLenNUm[i - 1][j]) {
//对于有分支的可能时,我们选取单方向
i--; //此结果对于结果1所选取方向,str1的下标左移一位.替换为j--,则结果对应与结果2选取的方向
}
}
}
//由于是从后往前加入字符的,需要反转才能得到正确结果
System.out.println(sb.reverse().toString());
}
}
结果:
5. 0-1背包问题
案例:
给定n个物品和一个载重量为M的背包,其中第i个物品的重量为Wi,其价值为Pi,应该如何从这n个物品中选择出一些物品装进背包,在不超过背包的载重量的情况下,使得背包中物品的价值达到最大。物品不可分割。
显然,对于0-1背包问题,当背包中的物品的价值达到最大时,背包不一定装满。
1>第一步就是划分子问题。
设(X1,X2,…,Xn)是n个物品的最优解,则(X2,X3,…,Xn)必是其子问题的最优解,这个子问题共有n-1个物品,背包载重量为M-W1X1。
即满足约束条件: <=M-W1X1,
且背包中的物品的价值达到最大,即:max( )。
2>第二步就是建立子问题的递推关系。
用一个二维数组m来保存问题的最优值,其数组元素m[i][j]定义为:从前面i个物品中选取物品装进载重量为j的子背包中所能获得的最大价值。
(1)当 i=0或j=0,即有m[i][j]=0.
(2)当 i>0,j>0,且Wi>j,即有m[i][j] = m[i-1][j]
(3)当 i>0,j>0,且Wi<=j
把物品装进背包,即有:m[i][j] = Pi + m[i-1][j-Wi]
不把物品i装进背包,即有:m[i][j] = m[i-1][j]
显然当Wi<=j时有和两种装法,这两种装法所获得的价值不一定相同,那么这时m[i][j]取哪种呢?
m[i][j]=max{ m[i-1][j], Pi+m[i-1][j-Wi] }

3>第三步就是以自底向上的方式计算。
计算m[i][j],i=1,2,3…n
对于给定的i,j=1,2,3…M
例:
设有5个物品,重量分别为(w1,w2,w3,w4,w5)=(2,2,6,5,4),各物品的价值分别为(p1,p2,p3,p4,p5)=(6,3,5,4,6),给定背包的载重量为m=10,下面给出了一个(n+1)(m+1)的表,用来存放从前面i个物品中选出物品装入载重量为j的背包中所能取得的最大价值。表中给出了一部分元素的值,试填写空白处的值,并构造该问题的最优解。
分析:
代码:
package com.sun.main;
import java.util.Scanner;
public class Package01 {
// N表示物体的个数,V表示背包的载重
int N,V;
//用于存储每个物体的重量,下标从1开始
private int[] weight;
//存储每个物体的收益,下标从1开始
private int[] value;
//二维数组,用来保存每种状态下的最大收益
private int[][] F;
public static void main(String[] args) {
Package01 zop = new Package01();
zop.init();
zop.Recursive();
}
public void init() {
Scanner sc = new Scanner(System.in);
System.out.println("输入物体个数:");
N = sc.nextInt();
System.out.println("输入背包空间数:");
V = sc.nextInt();
//下标从1开始,表示第1个物品
weight = new int[N + 1];
value = new int[N + 1];
F= new int[N + 1][V + 1];//注意是 N + 1,因为需要一个初始状态F[0][0],表示前0个物品放进空间为0的背包的最大收益
System.out.println("输入物体所占空间数:");
for(int i = 1; i <= N; i++) {
weight[i] = sc.nextInt();
}
System.out.println("输入每个物体的价值:");
for(int i = 1; i <= N; i++) {
value[i] = sc.nextInt();
}
}
public void Recursive() {
//对二维数组F进行初始化
int i,j;
for(j = 0; j <= V; j++) {
F[0][j] = 0;
}
//注意边界问题,i是从1开始的,j是从0开始的
//因为F[i - 1][j]中i要减1
for(i = 1; i <= N; i++) {
for(j = 0; j <= V; j++) {
//如果容量为j的背包放得下第i个物体
if(j >= weight[i]) {
F[i][j] = Math.max(F[i - 1][j - weight[i]] + value[i], F[i - 1][j]);
}else {
//放不下,只能选择不放第i个物体
F[i][j] = F[i - 1][j];
}
}
}
System.out.println("结果:"+F[N][V]);
}
}