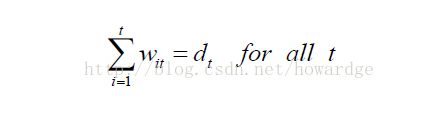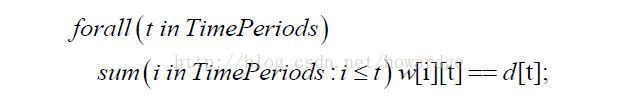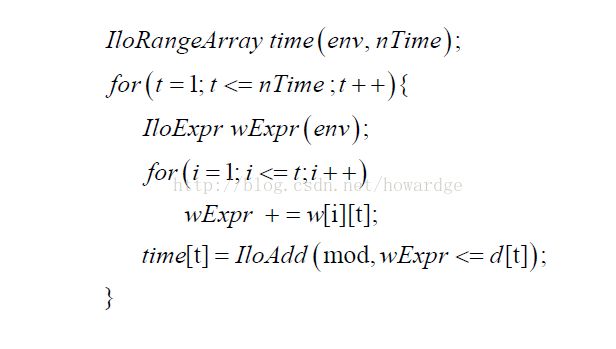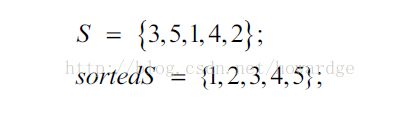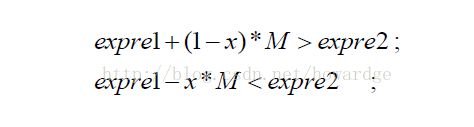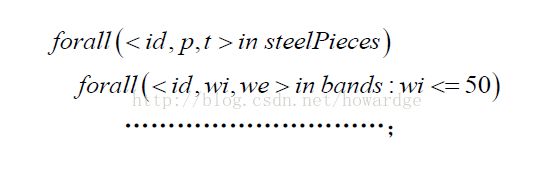OPL高效建模技巧

OPL的优势

OPL是ILOG团队为运筹学专家量身定制的一种优化建模语言，语法相对简单，约束定义接近运筹学专家习惯的属性模型表达。同时表达更为简洁，描述同样约束，OPL更为简单明了，易于检查排错。有助于开发者专注于模型的开发，而不必花很大精力将数学模型转换为复杂的程序语言。

以产能选址（UFL）为题为例，设 wit表示 i阶段生产的满足t 阶段需求的产量，dt 表示t 阶段的需求量，因此任一时间段，需求都必须满足的约束表达如下：

下面分以OPL和Concert（C++）两种建模语言表达如上约束。

l  OPL：

l  Concert（C++）：

 对比两种建模表达可见OPL更为简洁、方便，且更贴近数学模型；

集合（Sets）

OPL提供了更人性化更方便的集合供建模人员存储数据，集合的操作相比于传统的数组更为方便。集合的优势如下：

1、  建模人员可以用带有建模意义的字符串作为下标，方便理解模型；

2、  OPL提供了很多操作集合的API，方便建模人员更方便的操作数据，从而将主要精力花在数学建模层面，如OPL提供了集合的合并（union）、获取共同元素（inter）、和获取差异元素（diff）等很多函数；

3、  数组声明时必须给定长度，此后不可伸缩，数学建模时有时候需要不定长度的数据结构。集合则可根据需要动态改变大小，更加灵活。

API案例：

已知如下集合s1,s2  生成新的集合，生成两者共有元素集合 i={1}，两者的并集 u={1,2,3,4,5}、 s1中有而s2 没有的集合d={2，3} 和 s1和s2 中各自元素的并集sd={2,3,4} 。OPL代码如下，可见代码操作非常的简单方便。

同时OPL还提供了对集合的自动排序功能，方便建模人员对输入源数据进行快速处理。排序的关键词为 sorted，下面简单的演示下用法。

输出为：

集合可变元素案例：

结构体（Tuples）

结构体（Tuple）是OPL提供的一种多属性数据结构，与数据库中的一条记录（一行）相对应，方便建模人员与数据库进行读写操作。同时OPL支持以结构体为下标读取数组，以运输问题为例，我们的结果为供应商A 给客户B运输多少货，可以按照如下表达：

由此可见结构体更方便建模人员操作，变量的下标表达更为自然。同时也方便读写数据库，如上的结构体读数据库如下：

  

同样结构体和集合一样也提供了有序结构体（Sorted Tuples）。因为结构体对应于一条记录，因此结构体也提供主键功能，结构体对于其内记录的排序依靠自身的主键进行排序，示例如下：

输出的有序结构体 如下：

利用结构体可以帮建模人员因为数据稀疏而带来的变量个数巨大的问题。以上面的运输问题为例，假设有1000家仓库，1000家门店，不采用结构体采用二维数组则有1，000，000个决策变量（ routes[supply][demand]），同时采用结构体在约束表达上也更为简洁，示例如下：

由此可见结构体的表达更为简洁，且能够显著的降低变量的维度，带来了更高效的求解效率。

善用逻辑表达

OPL提供了很多处理逻辑的API函数，善用这些函数可以给建模节省很多时间同时提高模型的可读性和提高模型的求解性能。OPL支持逻辑与（&&）、逻辑或（||）、逻辑非（！）、条件约束（=>），三元表达式（a?b:c），利用这些逻辑表达式我们可以轻松表达模型中的非线性约束。

以常见的M法为例，设x 为决策变量， expre1和 expre2为两个决策变量构成的表达式，假设业务场景如下：

常规的数学建模思路是采用大M法来构建，但是M的取值很难定，一般都是根据实际模型情况定一个经验值，构建如下的数学表达式：

此种构造方式虽精妙，但是大M的设置比较随机，且模型的求解性对大M的设置值的敏感性很大。通过OPL的条件约束（=>）,我们可以轻松的避免大M法。OPL建模表达如下：

对比可见OPL的建模表达更易于解读和模型的后期维护，且避免了大M法带来的模型求解性能不稳定现象，因此推荐使用OPL的逻辑表达式来解决很多非线性的问题。

善用循环条件

构建数学模型中，我们常常会遇到筛选部分元素进行构建约束的需求，同时在实际中常常需要在两三个集合中通过公有元素过滤筛选部分集合元素进行施加约束。在进行这一类的循环筛选可用元素的操作时，比较初级的写法是分别循环每个集合，然后通过公有元素相等来实现，具体实现如下：

如上的表达可见对 bands进行了集合的遍历，筛选出idB==id 的集合，此种表达方式过于冗余，可以借用如下的方式获取更简洁和高效的表达（OPL内部也会将上述表达换成如下）：

善用热启动（warm start）

热启动为给模型设置一个初始解，让求解器在此解的基础上继续搜索。在求解大规模问题时或者时设计主模型、子模型迭代求解中，热启动被广泛采用。他能大大地提高模型的求解效率，缩短求解时间，提高解质量。

初始解的获得常见有两者方式：

1、  同一个模型先前的解；

2、  通过启发式或者约束规划求的部分解；

对于场景1，我们只需要获取同一个模型上一次解，OPL Script提供了现成的获取先前解的函数，具体实现如下：

对于场景2，我们只需提前设定以部分解，然后让引擎求解全部的决策变量，预先固定部分解也借助OPL的自带函数，具体实现如下：