最长递增序列的长度和序列；最长公共子序列

题目描述
（1）最长递增子序列的长度
对于一个数字序列，请设计一个复杂度为O(nlogn)的算法，返回该序列的最长上升子序列的长度，这里的子序列定义为这样一个序列U1，U2…，其中Ui < Ui+1，且A[Ui] < A[Ui+1]。
给定一个数字序列A及序列的长度n，请返回最长上升子序列的长度。
测试样例：
[2,1,4,3,1,5,6],7
返回：4

例如：一个序列有n个数：a[1],a[2],…,a[n]，求出最长递增子序列的长度。比如说对于测试数据5，3，4，8，6，7来说：
第一个数字5，d[0] = 1
第一个数字3，前面没有比他还小的了，d[1] = 1
第三个数字4，最长的递增子序列就是3，4，d[2] = 2
第四个数组8，d[3] = 3
第五个数字6，d[4] = 3
第六个数字7，d[5] = 4
思路：用c[i]来记录a[i]为结尾的子序列中最大递增子序列的长度，对于每一个i，令j从1到i - 1遍历，当a[j] < a[i]，比较当前c[i]和每一个c[j] + 1的大小，将最大值赋给c[i]。
O(n^2)时间复杂度的实现：

import java.util.*; 
public class AscentSequence {
    public int findLongest(int[] A, int n) {
        int [] c=new int[n];
        for(int i=0; i1;
            for(int j=0; jif(A[j]1, c[i]);
            }
        }
        int max=0;
        for(int i=0; iif(c[i]>max) max=c[i];
        }
        return max;
    }
}

O(nlogn)时间复杂度的实现：

import java.util.*;
public class AscentSequence {
    public int findLongest(int[] A, int n) {
        int[] B = new int[n+1]; B[1] = A[0];
        int len=1,start=0,end=len,mid;
        for(int i = 1;iif(A[i]>B[len]) {len++;B[len] = A[i];}
            else{
                start=1;end=len;
                while(start<=end){
                  mid=(start+end)/2;
                  if(B[mid]mid+1;
                  else end=mid-1;
              } B[start] = A[i];
            }
        }
        return len;
    }
}

（2）求以某个元素为结尾的最长递增序列
说明：本段代码实现的功能为
（1）随机生成一个有10个元素的数组，然后输出它的最长递增子序列
（2）输出以其中某一个元素为结尾的最长递增子序列的长度

import java.util.Arrays;
import java.util.Random;
public class LIS {
    public static void main(String[] args){
        System.out.println("generating a random array...");
        LIS lis=new LIS();
        int[] oldArray=lis.randomArray();
        for (int i = 0; i < oldArray.length; i++) {
            System.out.print(oldArray[i]+" ");
        }
        System.out.println();
        System.out.println("最长递增子序列的长度为");
        lis.lisGet(oldArray);

    public  int[] randomArray(){
        Random random=new Random();
        int[] randomArray=new int[10];
        for (int i = 0; i < 10; i++) {
            randomArray[i]=random.nextInt(10);
        }
        return randomArray;
    }

    public void lisGet(int[] arrayL ){
        int[] lisLength=new int[arrayL.length];//用于记录当前个元素作为最大元素的最长递增序列的长度
        for (int i = 0; i < arrayL.length; i++) { //初始化
            lisLength[i]=1;
        }
        int max=1;
        for (int i = 1; i < arrayL.length; i++) {
            for (int j = 0; j if (arrayL[j]1)>lisLength[i]) {                   
                    lisLength[i]=lisLength[j]+1;
                }
                if (max//得到当前最长递增序列的长度以及该子序列的最末元素的位置
                    max=lisLength[i];
                }           
            }
        }
        System.out.println(max);
        System.out.println("第i个元素结尾时最长递增子序列："+Arrays.toString(lisLength)); //输出数组
    }
}

（3）最长公共子序列
给定2个序列，求这两个序列的最长公共子序列，不要求子序列连续（序列中的数有先后顺序）。例如{2,4,3,1,2,1}和{1,2,3,2,4,1,2}的结果是{2,3,2,1}，{2,3,1,2}和{2,4,1,2}，也就是最长公共子序列长度唯一，但子序列不唯一。
下面这个图解释的很清楚

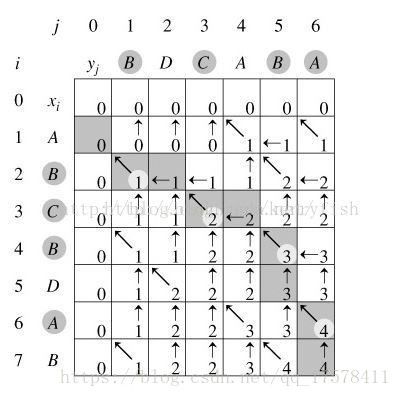
用d[i][j]表示序列a[0~i]和序列b[0~j]的最长公共子序列的长度，这是状态，对应上图中的数字。
状态转移方程：
当a[i] == b[j] 时，d[i][j] = d[i - 1][j - 1] + 1，re[i][j] = 0
当a[i] != b[j]时，有三种情况 ：
1.d[i - 1][j] > d[i][j - 1]，则d[i][j] = d[i - 1][j]，re[i][j] = 1

2.d[i - 1][j] < d[i][j - 1]，d[i][j] = d[i][j - 1]，re[i][j] = -1

3.d[i - 1][j] == d[i][j - 1]，d[i][j] = d[i][j - 1]，re[i][j] = 2
这里用re[i][j]来表示每个d[i][j]的方向来源，对应图中的箭头。0表示从d[i - 1][j - 1]转移而来，1表示从d[i - 1][j ]转移（图上表示为d[i][j]的左边大于上边），-1表示从d[i ][j - 1]转移，2表示d[i][j]的来源有两条路，即d[i][j - 1]或d[i - 1][j]转移，所以是输出所有结果（题例为3个）的关键。

输出函数prt()用的递归，用result[current_len]保存当前值（current_len初始值为前面计算出的最长长度len），这样可以保证是正序输出。

public class  Test{
    static int[][] d; // d[i][j]记录a[i]和b[j]的最长公共子序列长度，初始化为0
    static int[][] re; 
    static int len = 0; // 子字符串的长度
    static int count = 0; // 用于保存最长公共子字符串的个数
    static int[] result; // 用于暂时保存结果
    static int[] a;
    static int[] b;
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n1 = in.nextInt();
        int n2 = in.nextInt();
        a = new int[n1 + 1];
        b = new int[n2 + 1];
        for (int i = 1; i < a.length; i++) {
            a[i] = in.nextInt();
        }
        for (int i = 1; i < b.length; i++) {
            b[i] = in.nextInt();
        }
        result = new int[n1 + 1];
        d = new int[a.length][b.length];
        re = new int[a.length][b.length];

        len = dp(a, b);
        System.out.println("the length :" + len);
        prt(a.length - 1, b.length - 1, len);
        System.out.println("共有：" + count + "种");
        in.close();
    }

    public static int dp(int[] a, int[] b) {
        // initial
        for (int i = 0; i < a.length; i++) {
            d[i][0] = 0;
        }
        for (int i = 0; i < b.length; i++) {
            d[0][i] = 0;
        }
        for (int i = 1; i < a.length; i++) {
            for (int j = 1; j < b.length; j++) {
                if (a[i] == b[j]){
                    d[i][j] = d[i - 1][j - 1] + 1;
                    re[i][j] = 0;
                }
                else if (d[i][j - 1] < d[i - 1][j]){
                    d[i][j] = d[i - 1][j];
                    re[i][j] = 1; // 上方向
                }
                else if (d[i][j - 1] > d[i - 1][j]) { 
                    d[i][j] = d[i][j - 1];
                    re[i][j] = -1; // 左方向
                } else {
                    d[i][j] = d[i][j - 1];
                    re[i][j] = 2;  
                }
            }
        }
        return d[a.length - 1][b.length - 1];
    }
    public static void prt(int i, int j, int current_len) {
        if (i == 0 || j == 0) {
            for (int s = 0; s < len; s++) {
                System.out.print(result[s] + " ");
            }
            System.out.println();
            count++;
            return;
        }
        if (re[i][j] == 0) {
            current_len--;
            result[current_len] = a[i];
            prt(i - 1, j - 1, current_len);
        } else if (re[i][j] == 1) {
            prt(i - 1, j, current_len);
        } else if (re[i][j] == -1) {
                prt(i, j - 1, current_len);
        } else {
            prt(i - 1, j, current_len);
            prt(i, j - 1, current_len);
        }
    }
}