关系型数据库如何工作

关系型数据库如何工作

文章大概分为这三个部分、

• 低级和高级数据库组件的概述
• 查询优化过程的概述
• 事务和缓冲池管理的概述

基础

在硬件的发展还没像今天这么迅速时，开发人员必须知道他们正在编码的运算的确切数量。他们熟记自己的算法和数据结构，因为他们负担不起浪费CPU和内存的代价。在这一部分中，将阐述其中的一些概念，因为它们是理解数据库所必需的。我还将介绍数据库索引的概念。

O(1) vs O(n2)

现在，许多开发人员不关心时间复杂度……他们是对的!

但是，当您处理大量数据(不是几千行数据)或正在争取毫秒级的时间时，理解这个概念就变得非常重要了。你猜怎么着，数据库必须处理这两种情况!我不会让你厌烦很长时间，只是时间得到的想法。这将帮助我们以后理解基于成本的优化的概念。

概念

**时间复杂度用于查看算法处理给定数量的数据需要多长时间。**为了描述这种复杂性，计算机科学家使用数学大O符号。这个符号与一个函数一起使用，该函数描述了一个算法需要对给定数量的输入数据进行多少操作。

重要的不是数据量，而是当数据量增加时操作数增加的方式。时间复杂度并不能给出操作的确切数量，但这是个比较好的办法。

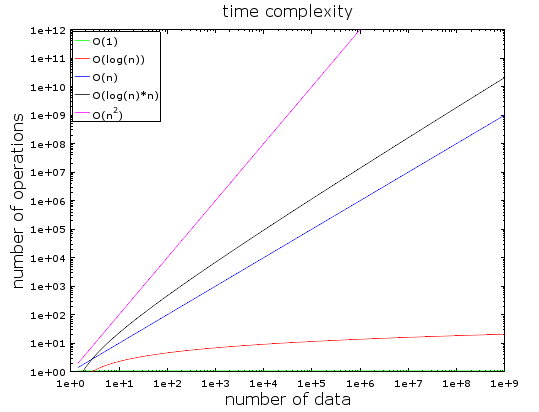
在这个图中，我们可以看到不同时间复杂度的算法随着数据数量的增加，操作次数的演变。数据的数量正在迅速从10亿增长到10亿。我们可以看到:

• O(1)或常数复杂度保持不变(否则就不叫常数复杂度)
• 即使有数十亿的数据，O(log(n))仍然很低
• 最糟糕的复杂度是O(n2)，其中操作的数量会迅速激增
• 另外两个复杂性正在迅速增加

Examples

如果数据量少，O(1)和O(n2)之间的差异可以忽略不计。例如，假设我们有一个需要处理2000个元素的算法。

• O(1)算法将需要一次运算
• O(log(n))算法需要7次运算
• O(n)算法需要2000次运算
• O(n*log(n))算法将需要14000个运算
• O(n2)算法将花费你4000000个运算

O(1)和O(n2)之间的差异似乎很大(400万)，但你最多会损失2毫秒，只是眨眼的时间。实际上，当前的处理器每秒可以处理数亿次操作。这就是为什么性能和优化在许多项目中不是一个问题。

就像我们前面说的一样，在面对大量数据时，了解这个概念仍然很重要。如果这一次算法需要处理1000000个元素(对于数据库来说不算大):

• O(1)算法将花费你一个运算
• O(log(n))算法需要14次运算
• O(n)算法将花费你100万次运算
• O(n*log(n))算法将花费14000000个运算
• O(n2)算法将花费你100000000000个运算

我没有做精确的计算，但我要说的是，对于O(n2)算法，我们有时间下楼拿个外卖了，如果我们在数据量上再加一个0，就有时间打个午觉了。

深入理解

• 在一个好的哈希表中进行搜索，会得到O(1)中的一个元素
• 在平衡良好的树中进行搜索，结果为O(log(n))
• 数组中的搜索结果为O(n)
• 最好的排序算法复杂度为O(n*log(n))
• 一个糟糕的排序算法有O(n2)复杂度

时间复杂度有多种类型:

• 一般的情况
• 最好的情况
• 最坏的情况

复杂性通常是最坏的情况。

我们只讲了时间复杂度但是复杂度也适用于:

• 算法的内存消耗
• 算法的磁盘I/O消耗

当然还有比n2更复杂的情况，比如:

• n4：后面我们会提到这个算法，已经是很再差劲了
• 3n：这个更差，我们将在本文中看到的一种算法具有这种复杂性(实际上在许多数据库中都使用了这种算法)
• n的阶乘: 即使数据量很少，也永远不会得到结果
• n的n次方：如果你最终面对的是如此复杂的局面，你应该问问自己，你是否应该学计算机，甚至是学工科

归并排序

当需要对集合排序时，应该怎么做?一般我们可以调用sort()函数。好的，回答得很好。但是对于数据库，我们必须了解sort()函数是如何工作的。

有几个很好的排序算法，所以我将重点介绍最重要的一个：归并排序。我们现在可能还不理解为什么对数据进行排序是很有用的，但是在学习查询优化部分之后，我们应该了解为什么排序数据是有用的。此外，理解合并排序将帮助我们以后理解一个称为**合并连接（merge join）**的公共数据库连接操作。

归并

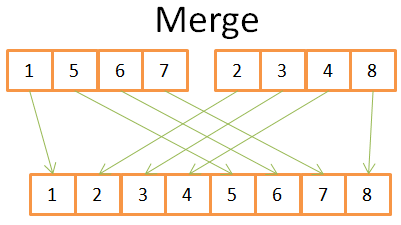
像许多有用的算法一样，归并排序基于一个技巧:将大小为N/2的两个排序数组合并到一个N元素排序数组只需要N个操作。这个操作称为归并。

让我们用一个简单的例子来归并排序怎么实现的:

从图中可以看出，为了构造最终的8个元素的排序数组，您只需要在2个4元素数组中迭代一次。因为这两个4元数组已经排序:

1. 比较两个数组中的两个当前元素(current=first，第一次)
2. 然后把最低的那个放到8个元素的数组中
3. 然后转到你取了最低的元素数组的下一个元素
4. 然后重复1,2,3，直到到达其中一个数组的最后一个元素
5. 然后将另一个数组的其余元素放入8个元素的数组中

这是可行的，因为两个4元素数组都是排序的，因此您不需要在这些数组中“返回”。

现在我们已经知晓了归并排序如何实现的，下面是归并排序的伪代码。

array mergeSort(array a)
 if(length(a)==1)
  return a[0];
 end if

//recursive calls
[left_array right_array] := split_into_2_equally_sized_arrays(a);
array new_left_array := mergeSort(left_array);
array new_right_array := mergeSort(right_array);

//merging the 2 small ordered arrays into a big one
result := merge(new_left_array,new_right_array);
return result;

归并排序将问题分解成更小的问题，然后找到更小问题的结果，从而得到初始问题的结果(注意:这种算法称为分治算法)。我认为这个算法是分为两个阶段的算法:

• 划分阶段，数组被划分成更小的数组
• 排序阶段，将小数组放在一起(使用merge)形成更大的数组。

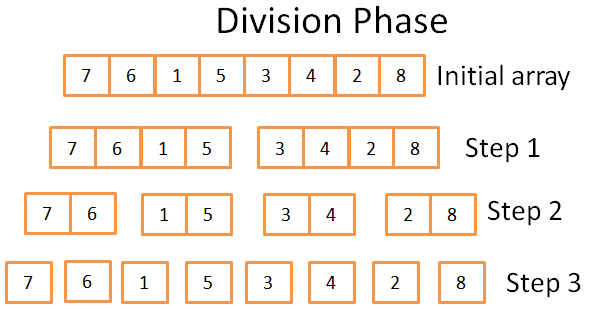
划分阶段

在划分阶段，使用3步将数组划分为单元数组。正式的步骤数是log(N)(因为N=8，所以log(N) = 3)。

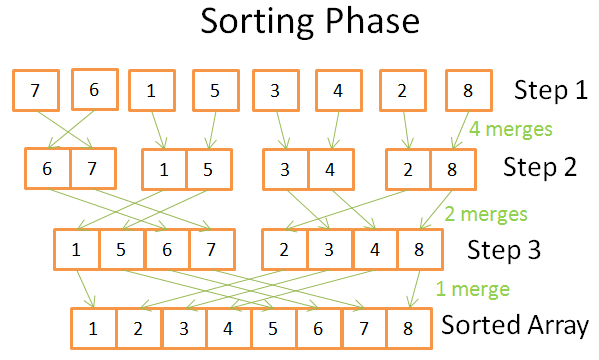
排序阶段

In the sorting phase, you start with the unitary arrays. During each step, you apply multiple merges and the overall cost is N=8 operations:

在排序阶段，从划分的最小数组开始。在每一步，我们应用多个归并的成本是N=8次操作:

• 在第一步中，有4个合并，每个合并需要2个操作
• 在第二步中，有两个合并，每个合并需要4个操作
• 在第三步中，你有一个需要8个操作的合并

因为有log(N)个步骤，所以总的时间复杂度是N*log(N)个操作。

优点

• 可以修改它以减少内存占用，方法是不创建新数组，而是直接修改输入数组(原地算法)
• 可以修改它，以便同时使用磁盘空间和少量内存，而不会造成巨大的磁盘I/O损失。其思想是在内存中只加载当前正在处理的部分。当您需要对一个几GB大的表进行排序时，而内存缓冲区只有100Mb大小时，这一点就非常重要（这种算法称为外部排序）
• 可以修改它以在多个进程/线程/服务器上运行。例如，分布式归并排序是Hadoop(大数据框架)的关键组件之一

数组，树和哈希表

既然我们已经理解了时间复杂度和排序背后的思想，我必须告诉你3种数据结构。这很重要，因为它们是现代数据库的支柱。之后我还将介绍数据库索引的概念。

数组

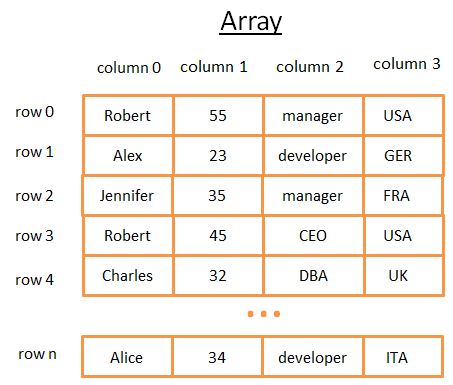
二维数组是最简单的数据结构。表可以看作一个数组。例如:

这个二维数组是一个包含行和列的表:

每一行代表一个主题，列是描述主题的特性。每个列存储特定类型的数据(整数、字符串、日期……)。虽然存储和可视化数据很好，但是当你需要查找特定的值时，它就很糟糕了。

例如，如果你想找到所有在英国工作的人，你必须查看每一行来确定这一行是否属于UK。这将花费你N个操作(N是行数)，这并不坏，但是有更快的方法吗?这就是tree发挥作用的地方。

注意:大多数现代数据库提供高级数组来有效地存储表，如堆组织的表或索引组织的表。但这并没有改变在一组列上快速搜索特定条件的问题。

树和数据库索引


这棵树有N=15个元素。假设我在找208:

• 我从键值为136的根开始。因为136<208，所以我查看节点136的右子树
• 398>208，我查看节点398的左子树
• 250>208，查看节点250的左子树
• 因此，我查看节点200的右子树。但是200没有右子树，这个值不存在(因为如果它确实存在，它就在200的右子树中)

现在假设我们在找40：

就像上面的过程一样，我们最终找到了40的节点。然后提取节点内的行id(它不在图中)，并查看表中给定的行id。知道行id让我知道数据在表中的确切位置，因此我可以立即获得它。最后，查找节点的算法复杂度是O(logN)，至少比O(N)强了很多。 : )

但是这个东西很抽象，所以我们回到我们的问题，我们要找的不是整数，而是表示上表中某个国家的字符串。假设你有一个包含“国家”列表格的树:

如果您想知道谁在英国工作，您可以查看树以获得“UK节点”中代表英国的节点，您将找到英国工人的行位置。刚才我们说的树就是索引。

你可以建立一个树索引对于任何列(可以使字符串,也可以是整数,也可以是整数和一个字符串或日期…),只要你有一个函数比较这些键(即作为索引的列),这样你就可以给这些键创建顺序(这是任何基本类型在数据库的情况）。

B+Tree Index

尽管这个树可以很好地获得一个特定的值，但是当你需要在两个值之间获取多个元素时，就会出现一个大问题。它将花费O(N)，因为你必须查看树中的每个节点，并检查它是否位于这两个值之间(例如，使用树的顺序遍历)。此外，这个操作对磁盘I/O不友好，因为必须读取整个树。我们需要找到一种有效地进行范围查询的方法。为了解决这个问题，现代数据库使用以前的树的一个修改版本，称为B+树。
B+树：

• 只有最低的节点(叶节点)存储信息(相关表中的行位置)
• 其他节点在这里只是为了在搜索期间路由到正确的节点


可以看到，节点更多(多了两倍)。实际上，还有其他节点，即“决策节点”，它将帮助您找到正确的节点(在关联的表中存储行位置)。但是搜索复杂度仍然是O(log(N))。最大的区别是，最低的节点与它们的后续节点相连。

在这个B+树中，如果你想找40到100之间的值:

• 您只需查找40(如果40不存在，则在40之后寻找最近的值)，就像前面的树所做的那样
• 然后收集40的继任者使用直接链接到继任者，直到你达到100

假设有M个结点，树有N个结点。对特定节点的搜索花费与前一棵树一样的log(N)。但是，一旦有了这个节点，在M操作中就会有M个后续操作，它们都有与其后续操作的链接。这个搜索只需要花费M + log(N)操作与前一个树的N个操作。此外，您不需要读取整个树(只需要M + log(N)个节点)，这意味着更少的磁盘使用。如果M很低(比如200行)而N很大(1000000行)，则会有很大的不同。

但新的问题又出现了。如果在数据库中添加或删除一行(在相关的B+树索引中如何操作？):

• 你必须保持B+树中节点之间的顺序，否则你将无法在混乱中找到节点
• 你必须在B+树中保持尽可能少的层数否则O(log(N))中的时间复杂度将变成O(N)

换句话说，B+树需要是自排序和自平衡的。幸运的是，通过智能删除和插入操作，这是可行的。但是这是有代价的:在B+树中的插入和删除是在O(log(N))的时间复杂度。这就是为什么有些人听说使用太多索引不是一个好主意。实际上，由于数据库需要对每个索引执行代价高昂的O(log(N))操作来更新表的索引，所以会减慢表中某一行的快速插入/更新/删除操作。此外，添加索引意味着事务管理器有更多的工作负载(后面我们会讲)

Hash table

最后一个重要的数据结构是哈希表。当我们希望快速查找值时，它非常有用。此外，理解哈希表将有助于我们以后理解称为哈希连接的公共数据库连接操作。数据库也使用此数据结构来存储一些内部内容(如锁表或缓冲池，稍后我们将看到这两个概念)

哈希表是一种数据结构，它可以快速找到具有其键值的元素。要建立一个哈希表，你需要定义:

• 每一个元素的键（Key）
• 键的哈希函数。哈希函数给了Key对应元素的位置(称为buckets)
• 比较键的函数。一旦找到了正确的bucket，就必须使用这个比较在bucket中找到要查找的元素

例子


这个哈希表有10个bucket。因为我很懒，我只画了5个桶但是我知道你很聪明，所以我让你想象其他5个。我使用的哈希函数是键的模10。换句话说，我只保留一个元素的键的最后一位来找到它的桶:

• 如果最后一位数字是0元素就会在桶0中结束
• 如果最后一位数字是1元素就会在桶1中结束
• 如果最后一位数字是2元素就会在桶2中结束
• …

比较函数就是简单地比较两个整数。
假设你想要得到78号元素：

• 哈希表计算78的哈希码，即8
• 然后在bucket 8中查找，找到的第一个元素是78
• 它会返回元素78
• 搜索只需要两个操作(一个用于计算散列值，另一个用于查找bucket内的元素)

现在，假设你想要得到元素59:

• 哈希表计算59的哈希码，即9
• 它在bucket 9中查找，找到的第一个元素是99；因为99!=59，所以元素99不是正确的元素
• 使用相同的逻辑，它查看第二个元素(9)、第三个元素(79)、…和最后一个元素(29)
• 元素不存在
• 搜索需要7次操作

很明显两次搜索的时间复杂度相差比较大，因为我们看到有很多bucket没有元素或很少，有的却很多，这就影响了我们的平均查找的时间复杂度。由此引出如何构建一个好的哈希函数来解决以上的问题。

什么是好的哈希函数

如果我现在用键的1000000的模(即取最后6位数字)来改变哈希函数，那么第二次搜索只需要一个操作，因为在bucket 000059中没有元素。真正的挑战是找到一个好的散列函数，它将创建包含非常少的元素的bucket。

在我的例子中，找到一个好的哈希函数是很容易的。但这是一个简单的例子，当我们的键是以下时，找到一个好的哈希函数很困难:

• String(例如一个人的姓)
• 2个String(例如一个人的姓和名)
• 2个String和一个Date(例如一个人的姓、名和出生日期)

使用好的哈希函数，在哈希表的查找的时间复杂度是O(1)。

数组vs哈希表

哈希表可以在内存中加载一半，而其他bucket可以留在磁盘上。对于数组，必须使用内存中的连续空间。如果要加载一个大的表，就很难有足够的连续空间。使用哈希表，你也可以选择所需的键(例如国家和一个人的姓)。

数据库概览

我们已经看到了数据库中的基本组件。我们现在需要退一步来看看数据库总体是什么样子。

数据库是一组可以方便地访问和修改的信息。但是一堆简单的文件也可以做到这一点。事实上，像SQLite这样最简单的数据库只不过是一堆文件。但是SQLite是一组精心制作的文件，因为它允许:

• 使用确保数据安全和一致的事务
• 即使处理数百万数据，也能快速处理数据

一般而言，数据库可以如下图所示:


网上有很多数据库的结构图，因此，不要过多地关注我如何组织这个数据库或如何命名这些过程，因为我做了一些选择来适应本文的计划。重要的是不同的组成部分;总体思想是将数据库划分为多个相互交互的组件。

核心组件：

• 进程管理器：许多数据库都有需要管理的进程/线程池。此外，为了获得纳秒级速度的提升，一些现代数据库使用自己的线程而不是操作系统线程
• 网络管理器：网络I/O是一个大问题，特别是对于分布式数据库。这就是为什么有些数据库有自己的管理器
• 文件系统管理器：磁盘I/O是数据库的第一个瓶颈。拥有一个能够完美地处理操作系统文件系统甚至替换它的管理器是很重要的
• 内存管理器:为了避免磁盘I/O的损失，需要大量的ram。但如果处理大量内存，则需要高效的内存管理器。特别是当您同时有许多使用内存的查询时
• 安全管理器：用于管理用户的身份验证和授权
• 客户端管理器：用于管理客户端连接

工具:

• 备份管理器:用于保存和恢复数据库
• 恢复管理器:用于在崩溃后以一致状态重新启动数据库
• 监听管理器:用于记录数据库的活动并提供监视数据库的工具
• 中央管理器:用于存储元数据(如表的名称和结构)，并提供管理数据库、模式、表空间的工具……

查询管理器:

• 查询解析器:检查查询是否有效
• 查询重写器:预先优化查询
• 查询优化器:优化查询
• 查询执行程序:编译和执行查询

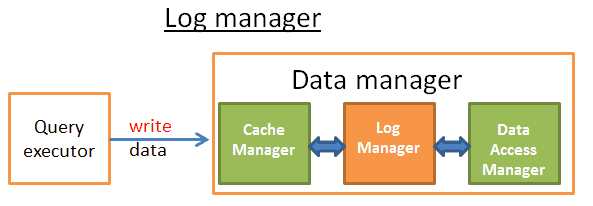
数据管理器:

• 事务管理器:处理事务
• 缓存管理器:在使用数据之前将数据放入内存，在将数据写入磁盘之前将数据放入内存
• 数据访问管理器:访问磁盘上的数据

在本文的其余部分，我将重点介绍数据库如何通过以下过程管理SQL查询:

• 客户端管理器
• 查询管理器
• 数据管理器

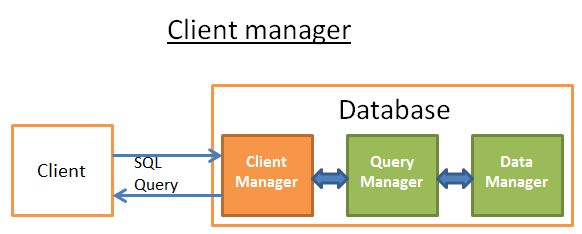
客户端管理器

客户端管理器是处理与客户端通信的部分。客户机可以是(web)服务器，也可以是终端用户/终端应用程序。客户端管理器提供了通过一组API访问数据库，如JDBC、ODBC等。

当你连接到一个数据库::

• 管理器首先检查您的身份验证(您的登录名和密码)，然后检查您是否具有使用数据库的授权。这些访问权限是由DBA设置的
• 然后，它检查是否有可用的进程(或线程)来管理查询
• 它还检查数据库是否处于高负载状态
• 它可以等待片刻来获得所需的资源。如果此等待达到超时，则关闭连接并给出可读的错误消息
• 然后它将您的查询发送到查询管理器，然后处理您的查询
• 由于查询处理不是“全有或全无”的事情，就是一下子就全部完成的事情，只要它从查询管理器获取数据，它就会将部分结果存储在缓冲区中，并开始将它们发送给您
• 如果出现问题，它会停止连接，给出可读的解释并释放资源

查询管理器

查询管理器就是数据库的强大所在。在这一部分中，一个写得不好的查询被转换成一个快速的可执行代码。然后执行代码并将结果返回给客户端管理器。这是一个多步骤的操作:

• 首先解析查询，看看它是否有效
• 然后重写它以删除无用的操作并添加一些预优化
• 然后对其进行优化以提高性能，并将其转化为执行和数据访问计划
• 然后进行编译
• 最后执行

在这一部分中，我不会过多地讨论最后两点，因为它们不太重要。

查询解析器

每个SQL语句都被发送到解析器，在那里检查语法是否正确。如果您在查询中出错，解析器将拒绝该查询。例如，如果你写的是“SLECT…”而不是“SELECT…”，那故事到此结束。不仅仅如此，它还检查关键字是否按正确的顺序使用。例如，WHERE在SELECT前的话就会被拒绝。

然后，分析查询中的表和字段。解析器使用数据库的元数据来检查:

• 表是否存在
• 表中的字段是否存在
• 是否可以对字段类型进行操作(例如，不能将整数与字符串进行比较，也不能对整数使用substring()函数))

然后，它检查您是否具有读取(或写入)查询中的表的授权。同样，这些表上的访问权限是由DBA设置的。在此解析过程中，SQL查询被转换为内部表示(通常是树)。如果一切正常，则将内部表示发送给查询重写程序。

查询重写器

在这一步，我们有一个查询的内部表示。改写的目的是:

• 预先优化查询
• 避免不必要的操作
• 以帮助优化器找到最佳的解决方案

重写器对查询语句执行一个已知规则列表。如果查询符合规则的模式，则应用规则并重写查询。以下是一个非详尽的(可选)规则列表:

• 视图合并：如果在查询中使用视图，则视图将使用视图的SQL代码进行转换
• 子查询的扁平化：要优化带有子查询的查询语句非常困难，所以重写器将尝试修改带有子查询的查询语句，这样可以删除子查询、

举个栗子

SELECT PERSON.*
FROM PERSON
WHERE PERSON.person_key IN
(SELECT MAILS.person_key
FROM MAILS
WHERE MAILS.mail LIKE 'christophe%');
Will be replaced by

SELECT PERSON.*
FROM PERSON, MAILS
WHERE PERSON.person_key = MAILS.person_key
and MAILS.mail LIKE 'christophe%';

• 删除不必要的操作符:例如，如果你使用DISTINCT，而你有一个防止数据不惟一的惟一约束，则会删除DISTINCT关键字
• 冗余连接消除:如果您有两个相同的连接条件，因为一个连接条件隐藏在视图中，或者根据传递性存在一个无用的连接，则将其删除
• 常量算术计算:如果你写的东西需要微积分，那么在重写的过程中它会被计算一次。例如，将AGE > 10+2转换为AGE > 12和TODATE(“some date”)转换为datetime格式的日期
• (高级)分区修剪:如果使用分区表，则重写器能够找到要使用的分区
• (高级)物化视图重写:如果有一个物化视图匹配查询中的谓词子集，则重写器检查该视图是否最新，并修改查询以使用物化视图而不是原始表
• (高级)自定义规则:如果有自定义规则来修改查询(如Oracle策略)，则重写器将执行这些规则
• (高级)Olap转换:分析/窗口函数、星型连接、rollup…也进行了转换(但我不确定这是由重写器还是优化器完成的，因为这两个过程都非常接近，它必须取决于数据库)

统计数据(Statistics)

在我们看到数据库如何优化查询之前，我们需要讨论一下统计数据，因为没有统计数据，数据库是愚蠢的。如果你不告诉数据库去分析它自己的数据，它就不会去做，并且会做出很糟糕的假设。

但是数据库需要什么样的信息呢?

我必须简要地谈谈数据库和操作系统如何存储数据。他们使用一个最小的单元，称为一个页面或一个块(默认情况下是4或8kb)。这意味着如果你只需要1kb，但它还是要花费你一页。如果页面占用8kb，那么将浪费7kb。

回到数据上来!当你要求数据库收集统计数据时，它会计算这样的值:

• 表中的行/页数
• 对于表中的每一列：
  • 不同的数据值
  • 数据值的长度(min、max、average)
  • 数据范围信息(min、max、average)
• 表的索引的信息

这些统计数据将帮助优化器估计查询的磁盘I/O、CPU和内存使用量。

每一列的统计数据非常重要。例如，如果需要在两个列上联接表PERSON: LAST_NAME、FIRST_NAME。通过统计数据，数据库知道FIRST_NAME上只有1000个不同的值，LAST_NAME上只有1000个不同的值。因此，数据库将联接LAST_NAME、FIRST_NAME而不是FIRST_NAME、LAST_NAME上的数据，因为它产生的比较要少得多，因为LAST_NAME不太可能是相同的，所以大多数情况下，对LAST_NAME的第2(或3)个字符进行比较就足够了。

但这些都是基本的统计数据。您可以要求数据库计算称为直方图的高级统计数据。直方图是关于列内值分布的统计信息。例如：

• 最常见的值
• 分位数
• 等等

这些额外的统计信息将帮助数据库找到更好的查询计划。特别是对于相等谓词(例如:AGE = 18)或范围谓词(例如:AGE > 10和AGE <40)，因为数据库可以更好地了解这些谓词所涉及的行数。

统计数据存储在数据库的元数据中。例如，你可以看到(非分区)表的统计:

• 对于Oracle在USER/ALL/DBA_TABLES 和 USER/ALL/DBA_TAB_COLUMNS
• 对于DB2在SYSCAT.TABLES 和 SYSCAT.COLUMNS

统计数字必须是最新的。没有什么比数据库认为一个表只有500行而它却有100000行更糟糕的了。统计数据的唯一缺点是计算它们需要时间。这就是大多数数据库默认情况下不会自动计算它们的原因。要计算数百万的数据是很困难的。在这种情况下，可以选择只计算基本统计信息，也可以选择计算数据库样本上的统计信息。

查询优化器

所有现代数据库都使用基于成本的优化(CBO)来优化查询。其思想是为每个操作设置一个成本，并通过使用开销最小的操作组合来获得结果，从而找到降低查询成本的最佳方法。

为了理解成本优化器是如何工作的，我认为最好有一个例子来“感受”这个任务背后的复杂性。在本部分中，我将向您介绍连接两个表的3种常见方法，我们很快就会发现，即使是一个简单的连接查询也很难优化。之后，我们将看到真正的优化器是如何完成这项工作的。

对于这些连接操作，我们将关注它们的时间复杂性，但是数据库优化器会计算它们的CPU成本、磁盘I/O成本和内存需求。时间复杂度和CPU成本之间的区别是，时间成本非常接近。对于CPU成本，我应该计算每一个操作，比如加法、“if语句”、乘法、迭代……

每个高级代码操作都有特定数量的低级CPU操作。CPU操作的成本是不一样的(就CPU周期而言)，无论你使用的是Intel Core i7、Intel Pentium 4还是AMD Opteron……换句话说，它取决于CPU架构。
利用时间复杂性更容易，我们仍然可以得到CBO的概念。我有时会讨论磁盘I/O，因为它是一个重要的概念。请记住，瓶颈大部分时间是磁盘I/O，而不是CPU使用。

索引

我们在讲B+树的时候讲过索引。只要记住这些索引已经排序了。另外，还有其他类型的索引，比如位图索引。它们在CPU、磁盘I/O和内存方面提供的成本与B+树索引不同。此外，如果可以提高执行计划的成本，许多现代数据库可以动态地为当前查询创建临时索引。

访问路径

在使用连接操作符之前，首先需要获取数据。下面是获取数据的方法。

注意:由于所有访问路径的真正问题是磁盘I/O，所以我们不会过多地讨论时间复杂性。

全扫描（Full scan）

如果你曾经看过什么是执行计划，那么一定见过单词full scan(或只是scan)。完全扫描就是数据库完全读取一个表或一个索引。就磁盘I/O而言，表全扫描显然比索引全扫描更昂贵。

范围扫描（Range Scan）

还有其他类型的扫描，如索引范围扫描。例如，当使用谓词“WHERE AGE > 20 AND AGE <40”时，可以使用它。当然，您需要在字段AGE上有一个索引来使用这个索引范围扫描。

我们在第一部分中已经看到，范围查询的时间成本类似于log(N) +M，其中N是这个索引中的数据数量，M是这个范围内的行数的估计。由于统计数据，N和M值都是已知的(注意:M是谓词AGE >20和AGE<40的选择性)。此外，对于范围扫描，您不需要读取完整索引，因此就磁盘I/O而言，它比完整扫描开销更小。

唯一扫描（Unique scan）

如果只需要索引中的一个值，可以使用惟一扫描。

按行id访问

大多数情况下，如果数据库使用索引，它必须查找与索引关联的行。为此，它将使用一个按行id进行的访问。

举个栗子，看下面这个查询语句

SELECT LASTNAME, FIRSTNAME from PERSON WHERE AGE = 28

如果你在age列上有一个索引，优化器将使用索引来查找所有age = 28的person，再找到表中的行(索引节点会存储行id信息等)，因为索引中的行只有年龄，但我们要查询他的lastname和firstname。

但是如果你执行下面的查询语句

SELECT TYPE_PERSON.CATEGORY from PERSON ,TYPE_PERSON
WHERE PERSON.AGE = TYPE_PERSON.AGE

PERSON上的索引将用于与TYPE_PERSON连接，但是表PERSON不会被行id访问，因为你没有查询这个表上的信息。虽然它对于一些访问非常有效，但是这个操作的真正问题是磁盘I/O。如果需要通过行id进行太多访问，数据库可能会选择全扫描。

连接运算符

我将介绍3个常见的连接操作符:合并连接、散列连接和嵌套循环连接。但在此之前，我需要介绍一些新的词汇:inner relation和outer relation。Relation 可以是:

• 一张表
• 一个索引
• 前一个操作的中间结果(例如前一个连接的结果)

当连接两个关系时，join算法以不同的方式管理这两个关系。在本文的其余部分，我将假设:

• outer relation是左数据集
• inner relation是右数据集

例如，A连接B是A和B之间的连接，其中A是outer relation，B是inner relation。

大多数情况下，A JOIN B的成本与B JOIN A的成本是不一样的。
在这一部分中，我还将假设外部关系有N个元素，内部关系有M个元素。请记住，一个真正的优化器通过统计信息知道N和M的值。

嵌套循环连接

嵌套循环连接是最简单的。

实现原理：

• 循环外部关系中的每一行
• 可以查看内部关系中的所有行，以查看是否有匹配的行

伪代码：

nested_loop_join(array outer, array inner)
  for each row a in outer
    for each row b in inner
      if (match_join_condition(a,b))
        write_result_in_output(a,b)
      end if
    end for
   end for

由于是两次循环，时间复杂度为O(N*M)

对于磁盘I/O，对于外部关系中的每N行，内部循环需要从内部关系中读取M行。这个算法需要从磁盘读取N + N*M行。但是，如果内部关系足够小，你可以把这个关系放在内存中，只需要读取M +N次。通过这种修改，内部关系必须是最小的那个数据集，因为它有更多的机会适应内存。

就时间复杂性而言，这没有什么区别，但就磁盘I/O而言，最好只读取一次这两个关系。当然，内部关系可以用索引代替，这对于磁盘I/O更好。

由于这个算法非常简单，所以如果内部关系太大而无法装入内存，这里有另一个版本，它对磁盘I/O更友好。这个想法是这样的:

• 不是逐行读取两个关系
• 一串一串地读它们，并在内存中保留两串行(从每个关系中)
• 可以比较这两个串中的行，并保持匹配的行
• 然后，从磁盘加载新的串并比较它们
• 如此循环，直到没有需要加载的束为止

// improved version to reduce the disk I/O.
nested_loop_join_v2(file outer, file inner)
  for each bunch ba in outer
  // ba is now in memory
    for each bunch bb in inner
        // bb is now in memory
        for each row a in ba
          for each row b in bb
            if (match_join_condition(a,b))
              write_result_in_output(a,b)
            end if
          end for
       end for
    end for
   end for

在这个版本中，时间复杂度保持不变，但是磁盘访问的次数减少了:

• 在以前的版本中，算法需要N + N*M次访问(每次访问获得一行)
• 在这个新版本中，磁盘访问的次数变成了number_of_bunches_for(外部)+ number_of_bunches_for(外部)* number_of_bunches_for(内部)
• 如果增加组的大小，就会减少磁盘访问的次数

Hash连接

哈希连接比较复杂，但在很多情况下，它的成本比嵌套循环连接要小。

哈希连接的思想是：

• 从内部关系中获取所有元素
• 建立一个内存中的哈希表
• 逐一获取外部关系的所有元素
• 计算每个元素的哈希值（用哈希表的哈希函数），找到内部关系的相关联的bucket
• 找一找桶中的元素与外表的元素是否匹配

在时间复杂性方面，我需要做一些假设来简化问题。

• 内部关系分为X个桶
• 哈希函数对这两个关系的哈希值分布几乎是均匀的。换句话说，这两个桶的大小是相等的
• 外部关系的一个元素与桶内的所有元素之间的匹配需要花费桶内元素的数量

时间复杂度为（M/X）N + cost_to_create_hash_table(M) + cost_of_hash_functionN

如果哈希函数创建了足够多的小尺寸桶，那么时间复杂度为O(M+N)

这里是另一个版本的哈希连接，它对内存更友好，但对磁盘I/O不那么友好。这一次是这样的：

• 计算出内部和外部关系的哈希表
• 然后把它们放到磁盘上
• 然后将2个关系桶逐桶比较(其中一个加载在内存中，另一个逐行读取)

归并连接

归并连接是唯一能产生排序结果的连接。

注意：在这个简化的合并连接中，没有内表和外表，它们的作用都是一样的。但真正的实现会有所区别，例如，在处理重复表时。

归并连接可以分为两个步骤。

• （可选）排序连接操作。两者的输入都是对join键进行排序。
• 归并连接操作。将排序后的输入合并在一起。

分类

我们已经讲到了归并排序，在这种情况下，归并排序是一个很好的算法（但如果内存不是问题的话，不是最好的）。

但是有时候数据集已经排序了，例如：

• 如果表是原生排序的，比如说一个索引组织的表，在join条件上的索引组织的表
• 如果该关系是连接条件上的索引
• 如果在查询过程中，这个连接应用于已经排序的中间结果上

归并连接

这一部分与我们看到的合并排序的归并操作非常相似。但这一次，我们不是从两个关系中挑选每一个元素，而是只从两个关系中挑选等价的元素。思路是这样的，

1. 你比较2个关系中的两个当前元素（current=first为第一次）
2. 如果它们相等，那么你把这两个元素都放在结果中，两个关系的指针就会都指向下一个元素，你就会进入到下一个元素中去处理这两个关系
3. 如果不是，你就去找值相对较小的关系的下一个元素
4. 并重复1,2,3，直到到达其中一个关系中的最后一个元素
   这样做是因为两个关系都是排序的，因此你不需要在这些关系中 “返回”。

这个算法是一个简化的版本，因为它没有处理同一数据在两个数组中多次出现的情况（换句话说就是多次匹配）。对于这种情况，真实版本的算法更复杂，这就是我选择简化版本的原因。

如果两个关系都已经排序了，那么时间复杂度是O(N+M)

如果两个关系都需要排序，那么时间复杂度就是对两个关系进行排序的成本。O(NLog(N) + MLog(M))

下面是多次匹配的情况的实现代码：

mergeJoin(relation a, relation b)
  relation output
  integer a_key:=0;
  integer b_key:=0;
  
  while (a[a_key]!=null or b[b_key]!=null)
    if (a[a_key] < b[b_key])
      a_key++;
    else if (a[a_key] > b[b_key])
      b_key++;
    else //Join predicate satisfied
    //i.e. a[a_key] == b[b_key]
 
      //count the number of duplicates in relation a
      integer nb_dup_in_a = 1:
      while (a[a_key]==a[a_key+nb_dup_in_a])
        nb_dup_in_a++;
         
      //count the number of duplicates in relation b
      integer dup_in_b = 1:
      while (b[b_key]==b[b_key+nb_dup_in_b])
        nb_dup_in_b++;
         
      //write the duplicates in output
       for (int i = 0 ; i< nb_dup_in_a ; i++)
         for (int j = 0 ; i< nb_dup_in_b ; i++)     
           write_result_in_output(a[a_key+i],b[b_key+j])
            
      a_key=a_key + nb_dup_in_a-1;
      b_key=b_key + nb_dup_in_b-1;
 
    end if
  end while

哪一种连接算法最好呢？

如果有一个最好的连接算法，我们就不会介绍这么多连接算法。这个问题是非常难抉择的，因为很多因素都会影响到，比如：

• 可用内存的大小：没有足够的内存，你可以告别强大的哈希连接（至少是全内存内的哈希连接）
• 2个数据集的大小：例如，如果你有一个大表和一个很小的表，嵌套循环连接会比哈希连接快，因为哈希连接有一个昂贵的哈希创建费用。如果你有2个非常大的表，那么嵌套循环连接将非常耗费CPU
• 索引的存在：在2个B+树索引的情况下，归并连接显然效率更高
• 如果需要对结果进行排序：即使你正在处理未排序的数据集，你可能会想使用一个成本很高的归并连接（带排序的），因为最后结果会被排序，你可以用另一个归并连接来处理结果（或者可能是因为查询用ORDER BY/GROUP BY/DISTINCT操作隐式或显式地要求排序的结果）
• 如果关系已经被排序：在这种情况下，归并连接是最好的选择
• 连接类型：是等价连接（即：tableA.col1 = tableB.col2）？是内联接、外联接、卡特尔乘积还是自联接？有些联接在某些情况下是不能工作的
• 数据的分布情况。如果join条件上的数据是偏斜的（例如你是以姓氏为条件加入的人，但很多人的姓氏都是一样的），使用哈希join将是一场灾难，因为哈希函数会产生分布不均匀的bucket
• 如果你想让连接由多个线程/进程执行

例子

我们刚刚介绍了三种类型的连接操作。

现在我们需要连接5个表，才能有一个人的完整视图。一个Person可以有：

• multiple MOBILES
• multiple MAILS
• multiple ADRESSES
• multiple BANK_ACCOUNTS

翻译成SQL语句就是

SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS
WHERE
PERSON.PERSON_ID = MOBILES.PERSON_ID
AND PERSON.PERSON_ID = MAILS.PERSON_ID
AND PERSON.PERSON_ID = ADRESSES.PERSON_ID
AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID

要优化这个查询语句，我必须找到最好的处理数据的方法。但是有2个问题。

• 我应该用什么样的Join算法来处理每个Join？

我有3种可能的Join（Hash Join、Merge Join、Nested Join），可以使用0,1或2个索引（更何况有不同类型的索引）

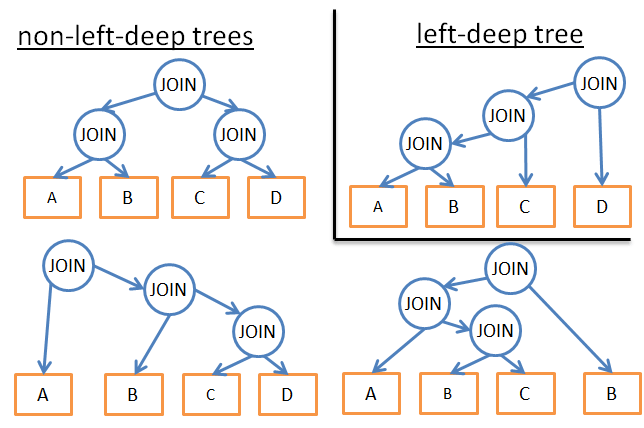
• 我应该选择什么顺序来计算加入？

例如，下图显示了4个表上用3个连接的不同可能方案

那么，下面是我的几种可能。

1. 我用暴力的方法
   利用数据库的统计，我计算出每一个可能的方案的成本，选择了最佳方案。但是，有很多可能性。对于一个给定的加入顺序，每个加入有3种可能。HashJoin，MergeJoin，NestedJoin。所以，对于给定的连接顺序，有34种可能性。连接顺序是一个二进制树上的排列组合问题，并且有(24)!/(4+1)! 可能的顺序。对于这个非常简化的问题，我最终得到34(2*4)!/(4+1)! 的可能性。
   用非专业术语来说，这意味着有27216种可能的计划。如果我现在再加上归并连接的可能性，即取0,1或2个B+Tree索引，可能的计划数就变成了210 000。我是不是忘了提一下，这个查询是非常简单的？

2. 我哭着退出这个工作
   很有诱惑力，但你不会得到你的结果，我需要钱来付账。

3. 我只试了几个方案，就选成本最低的那个
   因为我不是超人，我无法计算出每个计划的成本。相反，我可以从所有可能的计划中任意选择一个子集，计算出它们的成本，然后给出这个子集中最好的计划。

4. 我应用智能规则来减少可能的计划数量
   有2种类型的规则。

   我可以使用 "逻辑 "规则，这些规则会删除无用的可能性，但它们不会过滤掉很多可能的计划。比如说 “嵌套循环连接的内部关系必须是最小的数据集”

   我接受没有找到最好的解决方案，并应用更激进的规则来减少很多可能性。例如，“如果一个关系很小，就使用嵌套循环连接，千万不要使用合并连接或哈希连接”

在这个简单的例子中，我最终得到了很多可能性。但真正的查询可以有其他的关系运算符，如OUTER JOIN、CROSS JOIN、GROUP BY、ORDER BY、PROJECTION、UNION、INTERSECT、DISTINCT…这意味着更多的可能性。

那么，数据库是怎么做的呢？

动态规划、贪婪算法和启发式算法

一个关系型数据库尝试了我刚才说的多种方法。优化器的真正工作是在有限的时间内找到一个好的解决方案。

大多数时候，优化器并没有找到最好的解决方案，而是找到一个 "好的 "解决方案。

对于小的查询，做一个暴力的方法是可以的。但是有一种方法可以避免不必要的计算，这样即使是中等体量的查询也可以使用暴力方法。这就是所谓的动态编程。

动态规划

它们共享同一个（A JOIN B）子树。所以，我们可以不在每次计划中计算这个子树的成本，而是计算一次，将计算出的成本保存下来，当我们再次看到这个子树的时候，再重复使用。更正式的说，我们面临的是一个重叠问题。为了避免部分结果的额外计算，我们使用类似备忘录技术。

使用这种技术，我们不再有(2*N)!/(N+1)!的时间复杂度，而是只需要3^N。在我们之前的例子中，我们用4个连接，这意味着从336个排序传递到81个。如果你拿一个更大的查询，用8次接续（这并不大），这意味着从57 657 600传递到6561。

procedure findbestplan(S)
if (bestplan[S].cost infinite)
   return bestplan[S]
// else bestplan[S] has not been computed earlier, compute it now
if (S contains only 1 relation)
         set bestplan[S].plan and bestplan[S].cost based on the best way
         of accessing S  /* Using selections on S and indices on S */
     else for each non-empty subset S1 of S such that S1 != S
   P1= findbestplan(S1)
   P2= findbestplan(S - S1)
   A = best algorithm for joining results of P1 and P2
   cost = P1.cost + P2.cost + cost of A
   if cost < bestplan[S].cost
       bestplan[S].cost = cost
      bestplan[S].plan = “execute P1.plan; execute P2.plan;
                 join results of P1 and P2 using A”
return bestplan[S]

对于较大的查询，你仍然可以采用动态规划的方法，但要用额外的规则（或启发式算法）来消除可能性。

• 如果我们只分析某一种类型的方案（例如：左深树），我们最终会得到n*2ⁿ，而不是3ⁿ

• 如果我们添加逻辑规则来避免某些模式的计划(比如“如果一个表作为给定谓词的索引，不要尝试在表上而是在索引上进行归并连接”)，它将减少可能性的数量，而不会影响最佳可能的解决方案
• 如果我们在流上添加规则(比如“在所有其他关系操作之前执行连接操作”)，这样也减少了很多可能性

贪婪算法

但是对于一个非常大的查询或有一个很快要得到的答案(但不是一个非常快的查询)，使用另一种类型的算法，贪婪算法。

其思想是遵循规则(或启发)以增量方式构建查询计划。有了这个规则，贪婪算法就可以一步一步地找到问题的最佳解决方案。算法以一个连接开始查询计划。然后，在每个步骤中，算法使用相同的规则向查询计划添加一个新的连接。

让我们举一个简单的例子。假设我们有一个查询，它包含5个表(A、B、C、D和E)上的4个连接。让我们使用“使用成本最低的join”规则

• 我们任意从5个表中的一个开始(我们选A)
• 我们用A (A是内部关系或外部关系)计算每个连接的成本
• 我们发现A联接B的成本最低
• 然后我们计算每个连接的成本，结果是A连接B (A连接B是内部关系或外部关系)
• 我们发现(A JOIN B) JOIN C的代价最大
• 然后，我们用(A join B) join C的结果计算每个join的成本
• 在最后，我们找到了计划((A JOIN B) JOIN C) JOIN D) JOIN E)

因为我们任意地从A开始，我们可以对B应用相同的算法，然后是C，然后是D，然后是e，然后我们保持这个计划的最低成本。顺便说一下，这个算法有个名字，叫做最近邻算法。

我不会讲得太细，但是有了一个好的模型和一个Nlog(N)的排序，这个问题就很容易解决了。这个算法的代价是O(Nlog(N)) vs O(3^N)对于完整的动态规划版本。如果有一个包含20个连接的大查询，这意味着26 vs 3 486 784 401，一个很大的差异!

这个算法的问题是，我们假设如果我们保持这个连接并添加一个新连接，那么在两个表之间找到最佳连接将会给我们带来最佳成本。但是:即使A JOIN B给出了A、B和C之间的最佳成本,(A JOIN C) JOIN B可能比(A JOIN B) JOIN C的结果更好。为了改善结果，可以使用不同的规则运行多个贪婪算法，并保持最佳计划。

其他算法

如何找到最佳的可行方案是许多计算机科学研究者的一个活跃的研究课题。他们经常试图为更精确的问题/模式找到更好的解决方案。例如：

• 如果查询是星型连接(它是某种类型的多连接查询)，一些数据库将使用特定的算法
• 如果查询是并行查询，一些数据库将使用特定的算法

还研究了其他算法来代替动态规划的大量查询。贪婪算法属于一个更大的家族，称为启发式算法。贪心算法遵循一个规则(或启发式)，保留它在前一步找到的解决方案，并“附加”它来找到当前步骤的解决方案。有些算法遵循一个规则，并以循序渐进的方式应用它，但并不总是保持在前一步找到的最佳解决方案。它们都被称为启发式算法。

例如，遗传算法遵循一个规则，但最后一步的最佳解决方案往往不保持:

• 一个解决方案表示一个可能的完整查询计划
• 这一个完整的查询计划可能有P个分计划
• 0)P个查询计划是随机创建的
• 1)只有成本最低的计划才会被保留
• 2)这些最好的计划被混合在一起形成P个新计划
• 3)有些P计划是随机修改的
• 4)步骤1、2、3重复T次
• 5)然后从最后一个循环的P计划中保留最好的计划

适者生存法则。

数据库的优化是怎么实现的

但是，所有这些都是理论性的。因为我是开发人员而不是研究人员，所以我喜欢具体的例子。

让我们看看SQLite优化器是如何工作的。这是一个轻量级的数据库，所以它使用了一个简单的优化，基于一个附加规则的贪心算法来限制可能方案的数量:

• SQLite选择从不在交叉连接操作符中重新排序表
• 连接被实现为嵌套连接
• 外连接总是按照它们发生的顺序计算
• 。。。
• 在3.8.0版本之前，SQLite在搜索最佳查询计划时使用“最近邻”贪婪算法

自3.8.0版(2015年发布)以来，SQLite在搜索最佳查询计划时使用了“N近邻”贪婪算法。

让我们看看另一个优化器是如何工作的。IBM DB2就像所有的企业数据库一样，但是我将重点介绍这个数据库。如果我们查看官方文档，我们会了解到DB2优化器允许您使用7种不同级别的优化:

• 对连接使用贪婪算法
  • 0 -最小优化，使用索引扫描和嵌套循环连接，避免一些查询重写
  • 1 -低优化
  • 2 -全面优化
• 对连接使用动态规划
  • 3 -适度优化和粗略估计
  • 5 -充分优化，使用启发式算法的所有技术
  • 7 -完全优化类似于5，没有启发式算法
  • 9 -最大优化，不惜代价考虑所有可能的连接可能，包括笛卡尔积

我们可以看到DB2使用贪婪算法和动态规划。当然，由于查询优化器是数据库的主要功能，所以它们不会共享它们所使用的启发方法。

仅供参考，默认级别是5。默认情况下，优化器使用以下特征:

• 使用所有可用的统计信息，包括频率值和分位数统计信息
• 应用所有查询重写规则(包括物化查询表路由)，但计算密集型规则只在非常罕见的情况下适用
• 使用动态编程连接枚举，使用:
  • 复合内部关系的有限使用
  • 对涉及查找表的星型模式的笛卡尔积的有限使用
• 这里考虑了各种各样的访问方法，包括列表预取(注意:将会看到这是什么意思)、索引结束(注意:带索引的特殊操作)和物化查询表路由

默认情况下，DB2在连接排序中使用受启发法限制的动态规划。其他条件(GROUP BY、DISTINCT…)由简单的规则处理。

缓存查询计划

由于创建计划需要时间，大多数数据库将计划存储在查询计划缓存中，以避免对同一个查询计划进行无用的重新计算。这是一个很大的主题，因为数据库需要知道何时更新过时的计划。其思想是设置一个阈值，如果表的统计数据在这个阈值之上发生了变化，那么将从缓存中清除涉及该表的查询计划。

查询执行器

在这个阶段，我们有一个优化的执行计划。这个计划被编译成一个可执行的代码。然后，如果有足够的资源(内存、CPU)，则由查询执行程序执行。计划中的操作符(JOIN、SORT BY…)可以按顺序或并行方式执行;由执行器决定。为了获取和写入数据，查询执行器与数据管理器进行交互，这是本文的下一部分。

数据管理器

在这个步骤中，查询管理器执行查询并需要来自表和索引的数据。它要求数据管理器获取数据，但是有两个问题:

• 关系数据库使用事务模型。因此，不能在任何时候获取任何数据，因为其他人可能同时在使用/修改数据
• 数据检索是数据库中最慢的操作。因此数据管理器需要足够智能来获取和保存内存缓冲区中的数据

在本部分中，我们将了解关系数据库如何处理这两个问题。我不会讨论数据管理器获取数据的方式，因为这不是最重要的。

缓存管理器

正如我已经说过的，数据库的主要瓶颈是磁盘I/O。为了提高性能，现代数据库使用缓存管理器。

查询执行程序不是直接从文件系统获取数据，而是向缓存管理器请求数据。缓存管理器有一个称为缓冲池的内存缓存。从内存中获取数据极大地提高了数据库的速度。很难给出一个数量级，因为这取决于你需要做的操作:

• 顺序访问(例如:全扫描)vs随机访问(例如:按行id访问)
• read vs write

以及数据库使用的磁盘类型:

• 7.2k/10k/15k rpm HDD
• SSD
• RAID 1/5/…

但是我认为内存比磁盘快100到100000倍。

但是，这会导致另一个问题(与数据库一样……)。缓存管理器需要在查询执行器使用数据前之前获取内存中的相应的数据;否则，查询管理器必须等待来自慢速磁盘的数据。

cache预取

这个问题称为预取。查询执行器知道它需要的数据，因为它知道查询的完整流程，并且知道磁盘上的数据和统计信息。这个想法是这样的:

• 当查询执行器处理它的第一组数据时
• 它要求缓存管理器预加载第二组数据
• 当它开始处理第二组数据时
• 它要求CM预加载第三组数据，并通知CM可以从缓存中清除第一批数据。

CM将所有这些数据存储在其缓冲池中。为了知道数据是否仍然需要，缓存管理器添加了关于缓存数据的额外信息(称为锁存器(Latch))。

有时查询执行器不知道它需要什么数据，有些数据库不提供此功能。相反，它们使用推测性预取(例如:如果查询执行器请求数据1、3、5，它可能在不久的将来请求数据7、9、11)或顺序预取(在本例中，CM只是在请求的数据之后从磁盘加载下一个连续数据)。

为了监视预取的工作情况，现代数据库提供了一个称为缓冲区/缓存命中率的指标。命中率显示了在不需要访问磁盘的情况下，在缓冲区缓存中找到请求数据的频率。缓存命中率低并不总是意味着缓存不能正常工作。

但是，缓冲区是有限的内存。因此，它需要删除一些数据，以便能够加载新的数据。从磁盘和网络I/O的角度来看，加载和清除缓存是有代价的。如果你有一个经常执行的查询，那么总是加载然后清除此查询使用的数据将不会是有效的。为了处理这个问题，现代数据库使用缓冲区替换策略。

缓冲区替换策略

大多数现代数据库(至少SQL Server、MySQL、Oracle和DB2)使用LRU算法。

LRU是“最近最少使用”的意思。此算法背后的思想是将最近使用过的数据保存在缓存中，因此更有可能再次使用这些数据。
下面是个可视化的例子：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7YZRj5dt-1590130229147)(http://coding-geek.com/wp-content/uploads/2015/08/LRU-624x481.png)]

为了便于理解，我假设缓冲区中的数据没有被锁存器锁定(因此可以删除)。在这个简单的例子中，缓冲区可以存储3个元素:

• 1:缓存管理器使用数据1并将数据放入空缓冲区
• 2: CM使用数据4并将数据放入半装载的缓冲区中
• 3: CM使用数据3并将数据放入半装载的缓冲区中
• 4: CM使用数据9。缓冲区已满，因此数据1被删除，因为它是最近使用的数据。数据9被添加到缓冲区中
• 5: CM使用数据数据4已经在缓冲区中，因此它再次成为第一个最近使用的数据。
• 6: CM使用数据1。缓冲区已满，因此数据9被删除，因为它是最近使用的数据。数据1被添加到缓冲区中
  …

该算法运行良好，但存在一些局限性。如果在一个大表上有一个完整的扫描呢?换句话说，当表/索引的大小超过缓冲区的大小时，会发生什么情况?使用此算法将删除缓存中的所有以前的值，而来自完整扫描的数据可能只使用一次。

为了防止这种情况发生，一些数据库添加了特定的规则。例如，根据Oracle文档:

“For very large tables, the database typically uses a direct path read, which loads blocks directly […], to avoid populating the buffer cache. For medium size tables, the database may use a direct read or a cache read. If it decides to use a cache read, then the database places the blocks at the end of the LRU list to prevent the scan from effectively cleaning out the buffer cache.”

还有其他的可能性，比如使用LRU的高级版本LRU-K。例如，SQL Server使用LRU-K,设K =2。

这个算法背后的想法是考虑到更多的历史。对于简单的LRU(也就是K=1时的LRU-K)，算法只考虑数据最后一次使用的时间。LRU-K:

• 它考虑了数据最后使用的K次。
• 权重被放在数据被使用的次数上
• 如果将一组新数据加载到缓存中，则不会删除经常使用的旧数据(因为它们的权重更高)。
• 但是，如果旧数据不再使用，算法就不能将它们保存在缓存中。
• 因此，如果不使用数据，权重会随着时间减少。

权重的计算非常昂贵，这就是SQL Server只使用K=2的原因。对于可接受的开销，这个值执行得很好。

当然，还有其他的算法来管理缓存：

• 2Q (a LRU-K like algorithm)
• CLOCK (a LRU-K like algorithm)
• MRU (most recently used, uses the same logic than LRU but with another rule)
• LRFU (Least Recently and Frequently Used)

写缓冲区

我们只讨论了在使用数据之前读取数据的缓冲区。但是在数据库中，还可以使用写缓冲区来存储数据，并通过成批地将数据刷新到磁盘上，而不是逐个地写入数据并产生许多单独的磁盘访问。

请记住，缓冲区存储的是页面(最小的数据单元)，而不是行(这是一种逻辑/人为的数据查看方式)。如果页已被修改且未写入磁盘，则缓冲池中的页是脏的。有多种算法可以决定在磁盘上写入脏页面的最佳时间，但是它与事务的概念高度相关，这是本文的下一部分。

事务管理器

这一部分是关于事务管理器的。我们将看到这个过程如何确保每个查询在自己的事务中执行。但是在此之前，我们需要理解ACID事务的概念。

ACID

ACID事务是一个工作单元，它确保4件事情:

• 原子性:事务是“全有或全无”的。即使它持续10个小时，如果事务崩溃，状态会回到事务之前(事务被回滚)。
• 隔离性:如果两个事务A和B同时运行，执行相同的操作，无论A是否在事务B之前/之后/期间完成，事务A和事务B的结果必须相同。
• 持久性:一旦事务提交(即成功结束)，无论发生什么情况(崩溃或错误)，数据都会保留在数据库中。
• 一致性:只有有效的数据(在关系约束和功能约束方面)才写入数据库。一致性与原子性和隔离性有关。

在同一个事务期间，可以运行多个SQL查询来读取、创建、更新和删除数据。当两个事务使用相同的数据时，混乱就开始了。经典的例子是账户A向账户B转账。假设你有两笔交易:

• Transaction 1：从A账户中取出100美元并将其交给B账户
• Transaction 2：从A账户取出50美元并将其交给B账户

我们要的事物要符合ACID：

• 原子性确保无论在T1期间发生什么(服务器崩溃、网络故障……)，都不会出现从A中提取100美元而没有提供给B的情况(这种情况是不一致的状态)。
• 隔离性确保如果T1和T2发生在同一时间,最后将A会取出150美元，B得到150美元。例如,A取出了150美元，B只得到了50美元。因为T2的行为部分抹去T1(这种情况下也是一个不一致的状态)。
• 持久性确保在提交T1之后数据库崩溃时，T1不会凭空消失。
• 一致性确保了系统中钱的数量不会改变。

许多现代数据库并没有将纯隔离作为默认行为，因为它带来了巨大的性能开销。SQL规范定义了4个隔离级别:

• Serializable (SQLite中的默认行为):最高级别的隔离。同时发生的两个事务是100%隔离的。每个事务都有自己的“世界”。
• Repeatable read(MySQL中的默认行为):除了一种情况外，每个事务都有自己的“世界”。如果事务成功结束并添加了新数据，这些数据将在另一个仍然运行的事务中可见。但是，如果修改数据并成功结束，修改将在仍然运行的事务中不可见。因此，事务间隔离的中断只与新数据有关，而与现有数据无关。
  例如，如果事务a执行“SELECT count(1) from TABLE_X”操作，然后事务B在TABLE_X中添加并提交一个新数据，如果事务a再次执行count(1)操作，那么该值将不相同。
  这被称为幻像读取。
• Read committed (Oracle、PostgreSQL和SQL Server中的默认行为):这是一个可重复的Read +一个新的隔离。如果事务A读取数据D，然后事务B修改(或删除)并提交D，如果事务A再次读取数据D，它将看到B对数据所做的修改(或删除)。
  这称为不可重复读取。
• Read uncommitted:隔离的最低级别。这是一个读提交+打破隔离。如果事务A读取数据D，然后该数据D被事务B修改(未提交且仍在运行)，如果事务A再次读取数据D，它将看到修改后的值。如果事务B被回滚，那么由A第二次读取的数据D没有任何意义，因为它已经被一个从未发生过的事务B修改过(自从它被回滚以来)。
  这叫做脏读取。

大多数数据库都添加了自己的自定义隔离级别(比如PostgreSQL、Oracle和SQL Server使用的快照隔离)。而且，大多数数据库并没有实现SQL规范的所有级别(尤其是read uncommitted级别)。
在连接开始时，用户/开发人员可以覆盖默认的隔离级别(只需添加非常简单的一行代码)。

并发控制

确保隔离性、一致性和原子性的真正问题是对同一数据的写操作(添加、更新和删除):

• 如果所有事务都只是读取数据，那么它们可以同时工作，而不需要修改另一个事务的行为
• 如果(至少)其中一个事务正在修改其他事务读取的数据，那么数据库需要找到一种方法来对其他事务隐藏此修改。此外，它还需要确保这个修改不会被另一个没有看到修改数据的事务删除

这个问题称为并发控制。

解决这个问题最简单的方法是一个一个地运行每个事务(即顺序地)。但这是不可扩展的，而且只有一个内核在多处理器/核心服务器上工作，效率不是很高……

解决这个问题的理想方法是，每次创建或取消一个事务时:

• 监视所有事务的所有操作
• 检查两个(或更多)事务的部分是否冲突，因为它们正在读取/修改相同的数据
• 重新排序冲突事务中的操作，以减少冲突部分的大小
• 以一定的顺序执行冲突部分(而非冲突事务仍在并发地运行)
• 考虑到事务可否取消

更正式地说，这是一个日程安排冲突的日程安排问题。更具体地说，这是一个非常困难和CPU昂贵的优化问题。企业数据库承受不起为每个新事务事件寻找最佳调度而等待数小时的代价。因此，他们使用不太理想的方法，导致在冲突的事务之间浪费更多的时间。

锁管理器

为了处理这个问题，大多数数据库都使用锁和/或数据版本控制。因为这是一个很大的主题，所以我将重点讨论锁的部分，然后再谈一谈数据版本控制。

悲观锁

锁背后的想法是:

• 如果一个事务需要数据
• 它就锁住数据
• 如果另一个事务也需要这个数据
• 它就必须等到第一个事务释放数据。

这称为独占锁。

但是，为只需要读取数据的事务使用排他锁是非常昂贵的，因为它会迫使只想读取相同数据的其他事务等待。这就是为什么有另一种类型的锁，共享锁。

共享锁：

• 如果事务只需要读取数据A
• 它“共享锁定”数据并读取数据
• 如果第二个事务也只需要读取数据A
• 它“共享锁定”数据并读取数据
• 如果第三个事务需要修改数据A
• 它“独占锁定”数据，但它必须等到其他两个事务释放它们的共享锁，才能对数据A应用独占锁定

但是，如果数据是一个独占锁，那么只需要读取数据的事务就必须等待独占锁的结束，以便在数据上放置一个共享锁。

锁管理器是给出和释放锁的进程。在内部，它将锁存储在一个哈希表中(其中的键是要锁的数据)，并知道每个数据:

• 哪些事务正在锁定数据
• 哪些事务正在等待数据

死锁

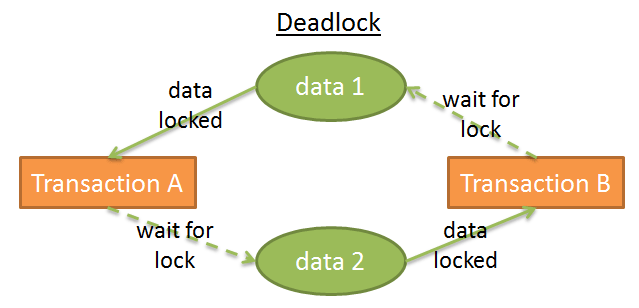
但是使用锁会导致两个事务永远等待一个数据:

在这个图:

• 事务A在data1上有一个独占锁，正在等待获取data2
• 事务B在data2上有一个独占锁，正在等待获取data1

这称为死锁。

在死锁期间，锁管理器选择取消哪个事务(回滚)，以消除死锁。这个决定并不容易:

• 是否最好终止修改最少数据量的事务(因此将产生最少代价的回滚)?
• 因为另一个事务的用户已经等待了更长的时间，所以终止等待时间更短的事务是否更好?
• 终止需要更少时间完成的事务(并避免可能的饥饿)是否更好?
• 在回滚的情况下，有多少事务将受到此回滚的影响?

但是在做出这个选择之前，它需要检查是否存在死锁。
可以将哈希表视为一个图(如前面的图所示)。如果图中有一个循环，就会出现死锁。由于检查周期的开销很大(因为包含所有锁的图非常大)，所以通常使用一种更简单的方法:使用超时。如果在此超时内没有给出锁，事务将进入死锁状态。

锁管理器还可以在提供锁之前检查这个锁是否会导致死锁。但同样地，完美地完成它需要很高的计算代价。因此，这些预先检查通常是一组基本规则。

锁协议

确保纯粹隔离的最简单方法是在事务开始时获取锁，并在事务结束时释放锁。这意味着事务必须等待所有的锁才能启动，事务持有的锁在事务结束时释放。它可以工作，但是会浪费很多时间来等待所有的锁。

更快的方法是两阶段锁定协议(DB2和SQL Server使用)，其中事务分为两个阶段:

• 执行阶段，事务可以获得锁，但不能释放任何锁
• 释放阶段，事务可以释放锁(对已处理且不再处理的数据)，但无法获得新锁

这两个简单规则背后的想法是:

• 释放不再使用的锁，以减少其他事务等待这些锁的等待时间
• 防止事务在事务启动后得到修改的数据，从而与事务获得的第一次数据不一致。

此协议可以正常工作，除非修改数据并释放关联锁的事务被取消(回滚)。你可能会遇到这样的情况:另一个事务读取修改后的值，而这个值将被回滚。为了避免这个问题，所有的独占锁必须在事务结束时释放。

当然，真正的数据库使用更复杂的系统，包括更多类型的锁(如意图锁)和更多粒度(行、页、分区、表、表空间上的锁)，但原理是一样的。

我只介绍了纯粹的基于锁的方法。数据版本控制是处理这个问题的另一种方法。
版本背后的想法是:

• 每个事务都可以在同一时间修改相同的数据
• 每个事务都有自己的数据副本(或版本)
• 如果两个事务修改相同的数据，则只接受一个修改，拒绝另一个修改，并且关联的事务将回滚(可能重新运行)。

它提高了性能，因为：

• 读事务不会阻塞写事务
• 写事务不会阻塞读事务
• 没有来自臃肿且速度很慢的锁管理器的开销

一切都比锁好，除非两个事务写相同的数据。此外，你会得到一个巨大的磁盘空间开销。

数据版本控制和锁是两种不同的观点:乐观锁和悲观锁。它们都有优点和缺点;这实际上取决于用例(更多的读和更多的写)。对于一个关于数据版本控制的演示，我推荐这个关于PostgreSQL如何实现多版本并发控制（MVCC）的非常好的演示。

有些数据库，如DB2(直到DB2 9.7)和SQL Server(快照隔离除外)只使用锁。其他像PostgreSQL, MySQL和Oracle使用了一种混合的方法，包括锁和数据版本控制。

如果你在不同的隔离级别上阅读这一部分，那么当你增加隔离级别时，你就增加了锁的数量，因此也就增加了事务等待它们的锁所浪费的时间。这就是大多数数据库在默认情况下不使用最高隔离级别(Serializable)的原因。

日志管理器

我们已经看到，为了提高性能，数据库将数据存储在内存缓冲区中。但是，如果在提交事务时服务器崩溃，你将在崩溃期间丢失仍然在内存中的数据，这会破坏事务的持久性。

我们可以在磁盘上写任何东西，但是如果服务器崩溃，最终会在磁盘上只写了一半的数据，这会破坏事务的原子性。

由事务执行的任何修改都必须撤消或完成。

解决这个问题有两种方法:

• 影子拷贝/页面:每个事务创建自己的数据库拷贝(或者只是数据库的一部分)，并处理这个拷贝。如果出现错误，则删除该副本。如果成功，数据库立即使用文件系统技巧切换来自副本的数据，然后删除“旧”数据。
• 事务日志:事务日志是一个存储空间。在每次写入磁盘之前，数据库将在事务日志上写入一个信息，以便在事务崩溃/取消时，数据库知道如何删除(或完成)未完成的事务。

当在涉及许多事务的大型数据库上使用影子复制/页面时，会产生巨大的磁盘开销。这就是现代数据库使用事务日志的原因。事务日志必须存储在稳定的存储中。我不会深入讨论存储技术，但是使用(至少)RAID磁盘是防止磁盘故障的必要手段。

大多数数据库(至少Oracle、SQL Server、DB2、PostgreSQL、MySQL和SQLite)使用Write-Ahead日志记录协议(WAL)处理事务日志。WAL协议是由3条规则组成的:

• 对数据库的每次修改都会产生一条日志记录，在将数据写入磁盘之前，必须将日志记录写入事务日志
• 日志记录必须按顺序书写;在日志记录B之前发生的日志记录A必须在B之前写入
• 当提交事务时，必须在事务成功结束之前将提交命令写入事务日志

这项工作由日志管理器完成。查看它的一个简单方法是，在缓存管理器和数据访问管理器(在磁盘上写入数据)之间，日志管理器在事务日志上写入每个update/delete/create/commit/rollback的操作，然后再将它们写到磁盘上。容易,对吧?

**显然不对!**在经历了这些之后，我们应该知道与数据库相关的所有内容都受到“数据库效应”的影响。更严重的问题是，如何在保持良好性能的同时编写日志。如果事务日志上的写操作太慢，则会降低所有操作的速度。

1992年，IBM的研究人员"发明"了一种增强版的WAL，称为ARIES。大多数现代数据库或多或少都在使用ARIES。逻辑可能不一样，但是ARIES背后的概念却无处不在。我之所以在发明后面加上引号，是因为根据MIT的这门课程，IBM的研究人员除了编写事务恢复的良好实践之外，什么也没做。

ARIES stands for Algorithms for Recovery and Isolation Exploiting Semantics.

这项技术的目的是双重的:

• 写日志时有着良好的性能
• 有着可靠和快速的恢复

数据库必须回滚事务的原因有很多:

• 因为用户取消了它
• 由于服务器或网络故障
• 因为事务破坏了数据库的完整性(例如，列上有一个惟一的约束，而事务添加了一个副本)
• 因为死锁

有时(例如，在网络故障的情况下)，数据库可以恢复事务。那这是怎么实现的呢？要回答这个问题，我们需要理解存储在日志记录中的信息。

事务期间的每个操作(添加/删除/修改)都会生成一个日志。该日志记录由以下部分组成:

• LSN：（A unique Log Sequence Number）唯一的日志序列号。这个LSN是按时间顺序给出的。这意味着如果操作A发生在操作B之前LSN (log A)就会小于LSN (log B)
• TransID：产生操作的事务的id
• PageID：修改后的数据在磁盘上的位置。磁盘上的最小数据量是一个页面，因此数据的位置就是包含数据的页面的位置
• PrevLSN：指向同一事务产生的前一个日志记录的链接。
• UNDO：一种消除操作影响的方法。例如，如果操作是update，UNDO将在更新之前存储更新元素的值/状态(物理 UNDO)，或者存储返回到前一状态的反向操作(逻辑 UNDO)
• REDO:一种重新执行操作的方法。同样地，有两种方法可以做到这一点。要么在操作之后存储元素的值/状态，要么重新执行操作。
• 仅供参考，一个ARIES日志还有另外两个字段:UndoNxtLSN和Type

而且，磁盘上的每个页面(存储数据，而不是日志)都有最后一个修改数据的操作的日志记录(LSN)的id。LSN的给定方式更加复杂，因为它与日志的存储方式相关联。但想法是一样的。

ARIES只使用逻辑UNDO，因为处理物理UNDO实在是一团糟。

注意:据我所知，只有PostgreSQL没有使用撤销。它使用一个垃圾收集器守护进程来删除旧版本的数据。这与PostgreSQL中数据版本控制的实现相关联。

每个日志都有一个唯一的LSN。被链接的日志属于同一个事务。日志按时间顺序链接(链表的最后一个日志是最后一个操作的日志)。

为了避免日志写入成为主要瓶颈，需要使用日志缓冲区。

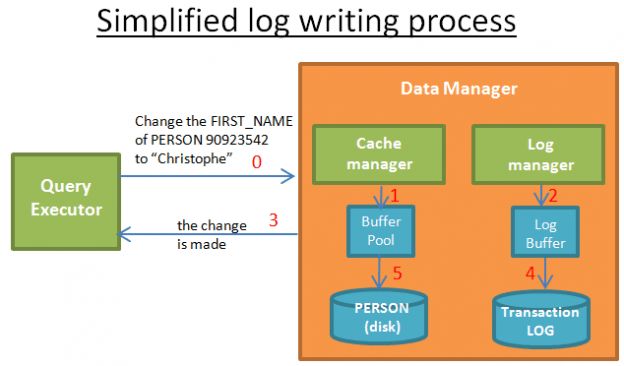
当查询执行器要求修改时:

• 1）缓存管理器将修改存储在其缓冲区中
• 2）日志管理器将相关日志存储在其缓冲区中
• 3）在这一步，查询执行器认为操作已经完成(因此可以请求其他修改)
• 4）然后(稍后)日志管理器将日志写入事务日志。何时写入日志是由算法决定的
• 5）然后(稍后)缓存管理器将修改写入磁盘。何时在磁盘上写入数据也是由算法决定的

当提交事务时，它意味着对事务中的每个操作执行步骤1、2、3、4、5。写入事务日志是快速的，因为它只是“在事务日志的某个地方添加了一个日志”，而在磁盘上写入数据则更为复杂，因为它是“以一种快速读取数据的方式写入数据”。

STEAL策略和FORCE策略

出于性能原因，第5步可能在提交之后执行，因为在发生崩溃的情况下，仍然可以使用REDO日志恢复事务。这被称为NO-FORCE。
数据库可以选择一个FORCE策略(即必须在提交之前执行步骤5)来降低恢复期间的工作负载。

另一个问题是选择数据是在磁盘上一步一步地写入(STEAL policy)，还是缓冲区管理器需要等到提交命令才立即写入所有内容(NO-STEAL)。在“STEAL”和“NO STEAL”之间进行选择取决于你想要什么:使用UNDO日志进行长时间恢复的快速写入还是快速恢复?

以下是这些策略对Recovery的影响的总结:

• STEAL/NO-FORCE需要UNDO和REDO:性能最高，但提供更复杂的日志和恢复过程(如ARIES)。这是大多数数据库的选择
• STEAL/FORCE只需要UNDO
• NO-STEAL/NO-FORCE只需要REDO
• NO-STEAL/FORCE不需要任何东西:最差的性能和大量的ram是必须的

Recovery

现在，我们有了很好的日志，让我们使用它们!假设新实习生破坏了数据库(规则1:这总是实习生的错)。重新启动数据库，恢复过程就开始了。

ARIES从崩溃中恢复过来需要三个步骤：

• 1）分析：恢复过程读取完整的事务日志，以重新创建崩溃期间发生的事件的时间线。它确定要回滚哪些事务(回滚所有没有提交命令的事务)以及崩溃时需要在磁盘上写入哪些数据
• 2）Redo：这一步从分析期间确定的日志记录开始，并使用REDO将数据库更新到崩溃前的状态。
  在redo阶段，REDO日志按时间顺序处理(使用LSN)。

对于每个日志，恢复过程读取磁盘上包含要修改的数据的页面的LSN。如果LSN(page_on_disk)>=LSN(log_record)，这意味着在崩溃之前已经在磁盘上写入了数据(但是该值被在日志之后和崩溃之前发生的操作所覆盖)，所以什么也不做。

如果LSN(page_on_disk)

即使对于将要回滚的事务，也会进行redo，因为它简化了恢复过程(但我相信现代数据库不会这样做)。

• 3）Undo：这一步回滚崩溃时未完成的所有事务。回滚从每个事务的最后一个日志开始，并按反时间顺序处理撤消日志(使用日志记录的PrevLSN)。

在恢复期间，必须警告事务日志有关恢复过程所做的操作，以便磁盘上写入的数据与事务日志中写入的数据同步。解决方案可能是删除正在撤消的事务的日志记录，但这非常困难。相反，ARIES在事务日志中写入补偿日志，逻辑上删除被删除事务的日志记录。

当一个事务被“手动”取消，或者被锁管理器取消(以停止死锁)，或者仅仅是因为网络故障，那么分析这一步就不需要了。事实上，关于REDO和UNDO操作的信息可以在2个内存表中找到:

• 事务表(存储所有当前事务的状态)
• 脏页表(存储需要在磁盘上写入的数据)

缓存管理器和事务管理器为每个新事务事件更新这些表。因为它们位于内存中，所以当数据库崩溃时它们就会被销毁。

分析阶段的工作是使用事务日志中的信息在崩溃后重新创建这两个表。为了加速分析过程，ARIES提供了检查点（CheckPoint）的概念。其思想是不时地在磁盘上写入事务表和脏页表的内容以及写入时的最后一个LSN，以便在分析过程中，只分析这个LSN之后的日志。

总结

• B+树索引的概述
• 数据库的全局概览
• 概述了基于成本的优化，重点介绍了连接操作符
• 缓冲池管理的概述
• 事务管理的概述

但是数据库包含更多的智能。例如，我没有谈论一些敏感的问题，比如：

• 如何管理集群数据库和全局事务
• 如何在数据库仍在运行时捕获快照
• 如何有效地存储(和压缩)数据
• 如何管理内存