动态规划算法梳理(Java)
今天看了一个公众号 (labulangdong)关于动态规划算法套路的详解,豁然开朗,在这里写一下自己的理解顺道自己再捋一捋思路。
原文链接:https://leetcode-cn.com/problems/coin-change/solution/dong-tai-gui-hua-tao-lu-xiang-jie-by-wei-lai-bu-ke/
一:原理
动态规划问题一般是要求最值,那么我把所有结果穷举出来最值不就出来了吗。事实上动态规划的核心问题就是穷举。
那为什么动态规划那么难呢?因为它具有三种特殊的要素:重叠子问题、最优子结构和状态转移方程。
①:如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。
② :用动态规划求解最优化问题的第一步就是刻画最优解的结构,如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个很好的线索。
③:动态规划中本阶段的状态往往是上一阶段状态和上一阶段决策的结果,函数表示前后阶段关系的方程,称为状态转移方程。事实上状态转移方程直接代表着暴力解法。写出状态转移方程是动态规划最难的地方。
二:斐波那契数
我们从LeetCode 509 斐波那契数这个简单的问题入手
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.给定 N,计算 F(N)。(0 ≤ N ≤ 30)
普通的递归算法,很好理解,长下面这个样子:
public class Solution {
public int fib(int N) {
if (N <= 1) {
return N;
}
return fib(N-1) + fib(N-2);
}
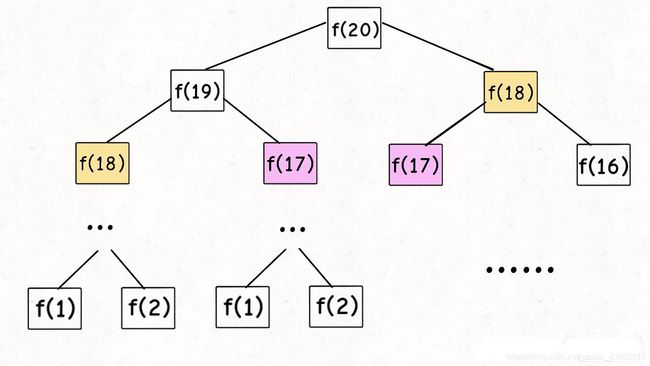
}画出它的递归树
我们可以看出其中存在大量的重复运算 ,比如f(18) f(17)在递归中都要运算两次......使得算法变得低效,时间复杂度=子问题个数*解决子问题的时间=O(2^N)。
这就是动态规划的第一个特殊要素:重叠子问题 。解决这一问题的方法:备忘录 或 DP table.
1、备忘录
对于大量的重复计算,我们选择造一个备忘录,对于每一层递归的答案,我们不急着返回,而是把它存在备忘录中。遇到子问题先去备忘录中查询是否有答案,如果有就直接返回结果。一般使用一个数组充当这个备忘录,当然也可以使用哈希表(字典)。
使用备忘录的自顶向下的递归解法
class Solution {
private Integer[] cache = new Integer[31];
public int fib(int N) {
if (N <= 1) {
return N;
}
cache[0] = 0;
cache[1] = 1;
return memoize(N);
}
public int memoize(int N) {
if (cache[N] != null) {
return cache[N];
}
cache[N] = memoize(N-1) + memoize(N-2);
return memoize(N);
}
}① 时间按复杂度:O(2^n)→O(n)
递归树经过了“剪枝”操作,子问题个数变成了O(n),所以时间复杂度就变成了O(n)。
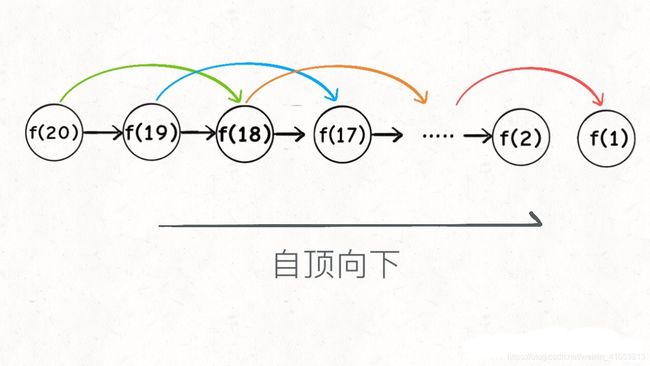
② 什么叫自顶向下?
我们从上层最大的问题开始,逐层分解,直到f(1)、f(2)打到底部返回。这就是自顶向下。
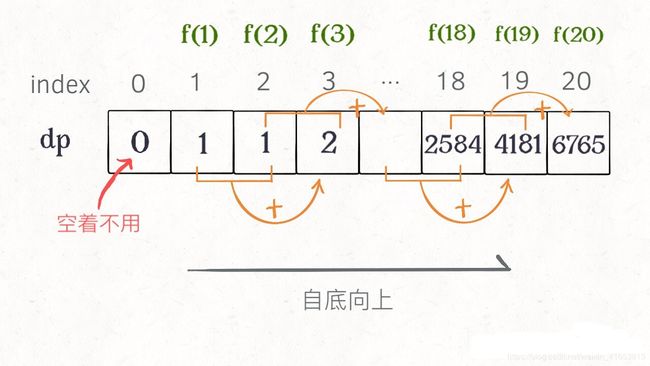
2、DP table
有了上面的备忘录的实现,我们可以将备忘录拿出来做成一张表,从而实现自底向上的递归解法。
class Solution {
public int fib(int N) {
if (N <= 1) {
return N;
}
return memoize(N);
}
public int memoize(int N) {
int[] cache = new int[N + 1];
cache[1] = 1;
for (int i = 2; i <= N; i++) {
cache[i] = cache[i-1] + cache[i-2];
}
return cache[N];
}
}实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
在这里解释一下状态转移方程:把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移。上面的几种解法中的所有操作都是围绕这个方程式的不同表现形式。
最后,其实我们还可以进一步优化空间复杂度。我们只需要三个变量来存储 fib(N), fib(N-1) 和 fib(N-2)。从而使空间复杂度变为O(1)。
class Solution {
public int fib(int N) {
if (N <= 1) {
return N;
}
if (N == 2) {
return 1;
}
int current = 0;
int prev1 = 1;
int prev2 = 1;
for (int i = 3; i <= N; i++) {
current = prev1 + prev2;
prev2 = prev1;
prev1 = current;
}
return current;
}
}因为斐波那契数列没有求最值,所以在斐波那契数的例子里没有涉及到到最优子结构的问题。
二:零钱兑换
使用 LeetCode 322题:
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1这里就这涉及到了最优子结构问题。关于最优子结构问题,这里公众号给的比喻通俗易懂的就离谱好吧。
“要符合「最优子结构」,子问题间必须互相独立。啥叫相互独立?
比如说,你的原问题是考出最高的总成绩,那么你的子问题就是要把语文考到最高,数学考到最高…… 为了每门课考到最高,你要把每门课相应的选择题分数拿到最高,填空题分数拿到最高…… 当然,最终就是你每门课都是满分,这就是最高的总成绩。
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,“每门科目考到最高”这些子问题是互相独立,互不干扰的。”
那么我们如何列出状态转移方程呢?
①:确定状态 ,也就是原问题和子问题中变化的变量。由于硬币数量无限,所以唯一的状态就是目标金额 amount
②:然后确定 dp 函数的定义:当前的目标金额是 n,至少需要 dp(n) 个硬币凑出该金额
③:然后确定「选择」并择优,也就是对于每个状态,可以做出什么选择改变当前状态。具体到这个问题,无论当的目标金额是多少,选择就是从面额列表 coins 中选择一个硬币,然后目标金额就会减少
④:最后明确 base case,显然目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1:
至此就得到了状态转移方程:
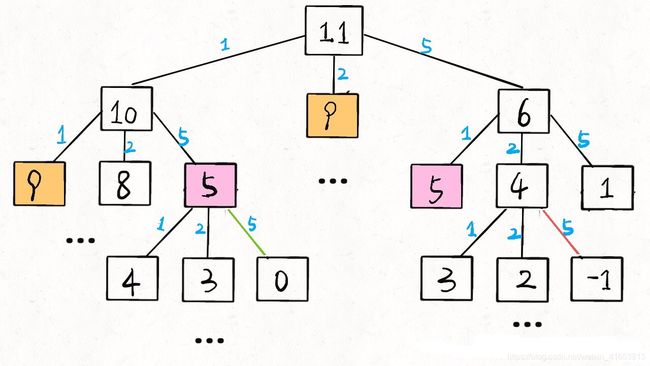
普通的递归树如下:
这里代码就直接贴了。
自底向上:
public class Solution {
public int coinChange(int[] coins, int amount) {
int max = amount + 1;
int[] dp = new int[amount + 1];
Arrays.fill(dp, max);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int j = 0; j < coins.length; j++) {
if (coins[j] <= i) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
}dp[i] = x 表示,当目标金额为 i 时,至少需要 x 枚硬币。
dp 数组初始化为 amount + 1 :因为凑成 amount 金额的硬币数最多只可能等于 amount(全用 1 元面值的硬币),所以初始化为 amount + 1 就相当于初始化为正无穷,便于后续取最小值。
三、结论
结论是,遇到题还是不会做。唉,继续多刷题吧。