张量网络算法基础（二、量子态、量子算符）

从这篇博客开始慢慢接触到张量网络的基础算法了。我是一只正在不断学习、希望早日成为小白的小小白，有什么错误欢迎大家批评指正，喜欢的请点个赞哦！

量子态与量子算符

1. 定义

态矢（state vector）：代表量子态的状态，可标记为 $|\phi ⟩$。
正如大家耳熟能详的薛定谔的猫，猫活着的状态、猫死去的状态和猫处于既死又生的状态，这些都是量子态。一般下情况下，我们把猫活着的状态记为 $|1⟩$，猫着死去的状态记为 $|0⟩$，$|\phi ⟩$只是用来表示量子态的状态的符号，如果看见不一样表示的不必去纠结。

算符/算子（operator）：对态矢或算子的操作，可标记为 $O$。
如果我们只看算符的解释，对于算符的本质还是会感到很迷糊，其实，算符就是一种模型。我们可以这样子去进行理解，把算符当成一个加工厂，当一个态进入这个加工厂，出去的时候就变成另外一个态，而这个加工也正是算符对态作用。

基矢：定义为一组满足正交完备性的态矢 $\{|i⟩\}$。
态矢我们前面已经了解了，那么什么是具有正交完备性的态矢呢？像我们数学里面学的两个垂直的单位向量具有正交性，此时向量的内积等于0。基矢满足正交完备性，此时基矢的内积也等于0。也就是说当两个态矢的内积等于0时，它们就是一组满足正交完备性的态矢。我们将态矢的内积定义为
$$⟨i\mid i^{\prime }⟩={\delta }_{i{i}^{\prime }}$$

$\text{ 当 }i=i^{\prime }\text{ 狄拉克矩阵 }{\delta }_{i{i}^{\prime }}=1,\text{ 否则 }{\delta }_{i{i}^{\prime }}=0$。

对于一个单自旋体系，我们所能观测到的只有两种情况，就像死猫和活猫那样，单自旋体系的基矢我们一般用 $\{|0⟩\}$和 $\{|1⟩\}$来表示。任意的单自旋量子态可写成基矢的线性叠加:
$$|\phi ⟩={\phi }_0|0⟩+{\phi }_1|1⟩=\sum _{i=0}^1{\phi }_i|i⟩$$

对于双自旋体系，基矢定义为
$$|0⟩|0⟩,|0⟩|1⟩,|1⟩|0⟩,|1⟩|1⟩$$

其中, $|i⟩|j⟩=|ij⟩=|i⟩\otimes |j⟩$ ，其构成的基矢为四个4维向量。例如$|1⟩={\left[\begin{array}{cc}1& 0\end{array}\right]}^T,|11⟩={\left[\begin{array}{cc}1& 0\end{array}\right]}^T\otimes {\left[\begin{array}{cc}1& 0\end{array}\right]}^T={\begin{array}{llll}[1& 0& 0& 0\end{array}]}^T$ 。
和单自旋量子态一样，任意的二自旋量子态可写成基矢的线性叠加:
$$|\phi ⟩={\phi }_{00}|00⟩+{\phi }_{01}|01⟩+{\phi }_{10}|10⟩+{\phi }_{11}|11⟩=\sum _{ij=0}^1{\phi }_{ij}|ij⟩$$

二自旋量子态 $|\phi ⟩$的系数可看作是$4\times 1$的向量${\left[\begin{array}{cccc}{\phi }_{00}& {\phi }_{01}& {\phi }_{10}& {\phi }_{11}\end{array}\right]}^T$, 也可以看作 $2\times 2$ 的矩阵 $\left[\begin{array}{cc}{\phi }_{00}& {\phi }_{01}\\ {\phi }_{10}& {\phi }_{11}\end{array}\right]$, 二者相差一个reshape操作。

补充：$\otimes$ 称为直积、张量积、外积或克伦内克积,$\otimes$符号可省略

2. 态矢与算符的向量或矩阵表示

学完下面的内容，你会慢慢发现张量和和数学是紧密联系在一起的。

态矢和在给定基矢下的展开系数的向量表示

由前面的学习我们可以知道任意单个自旋的量子态可写成基态的线性叠加:
$$|\phi ⟩={\phi }_0|0⟩+{\phi }_1|1⟩$$

在不引起误解的情况下我们可以直接认为态即对应的系数向量.
例如 $|\phi ⟩={\phi }_0|0⟩+{\phi }_1|1⟩$, 我们可以认为 $|\phi ⟩=\left[\begin{array}{ll}{\phi }_0& {\phi }_1\end{array}\right]$ , 此时若 $|\phi ⟩=|1⟩$, 即 $|1⟩={\phi }_0|0⟩+{\phi }_1|1⟩\Rightarrow {\phi }_0=0,{\phi }_1=1,$则 $|1⟩={\left[\begin{array}{ll}0& 1\end{array}\right]}^T$ 。一般情况下，我们认为左矢 $⟨\phi |$ 对应于行向量，右矢$|\phi ⟩$对应于列向量，$⟨\phi |$为$|\phi ⟩$的共轭转置。

量子态内积对应于系数向量的内积:
$$⟨\phi \mid \psi ⟩=\left[\begin{array}{cc}{\phi }_0& {\phi }_1\end{array}\right]{\left[\begin{array}{ll}{\psi }_0& {\psi }_1\end{array}\right]}^T$$

我们可以试着用前面学过的知识去证明一下这个等式：
证明:
因为$|\phi ⟩={\sum }_i{\phi }_i|i⟩,|\psi ⟩={\sum }_j{\psi }_j|j⟩$
有$⟨\phi \mid \psi ⟩={\sum }_{ij}{\phi }_i^{\ast }{\psi }_j⟨i\mid j⟩$
由基矢的正交归一性 $⟨i\mid j⟩={\delta }_{ij}$
令 $j$=$i$, 有 ${\sum }_{ij}{\phi }_i^{\ast }{\psi }_j⟨i\mid j⟩={\sum }_i{\phi }_i^{\ast }{\psi }_i$
证毕

算符在给定基矢下的展开系数的矩阵表示

基矢的向量表示确定之后，可用这对基矢对算符做展开，得到算符的系数。例如泡利算符的展开系数是一个2 × 2的矩阵，它满足
$${\hat{\sigma }}^{\alpha }=\sum _{ij=0}^1{\sigma }_{ij}^a|i⟩⟨j|(a=x,y,z)$$
$\text{我们由 }{\hat{\sigma }}^{\alpha }={\sum }_{ij=0}^1{\sigma }_{ij}^a|i⟩⟨j|$以及基矢的正交归一性，易得
$${\sigma }_{ij}^a=⟨i\left|{\hat{\sigma }}^{\alpha }\right|j⟩$$

看到这不知道有没有小伙伴觉得一点也不易得，反正当时我第一次看是这么想的，我们在这个中间加一步，看这：
$$⟨i|{\hat{\sigma }}^{\alpha }|j⟩=\sum _{i=0}^1{\sigma }_i^a⟨i||i⟩⟨j||j⟩\Rightarrow {\sigma }_{ij}^a=⟨i\left|{\hat{\sigma }}^{\alpha }\right|j⟩$$

这样子是不是就明白啦！

3. 量子态和算符的运算

在没学习态矢与算符的向量和矩阵表示之前对于量子态和算符的运算是不是一头雾水？学习了之后，在给定基矢、确定量子态和算符的向量与矩阵表示之后，相关的计算就自然而然变成与之对应的向量与矩阵的运算。
例如：定义上升算符 ${\hat{\sigma }}^{+}$和下降算符 ${\hat{\sigma }}^{-}$, 其在 ${\hat{\sigma }}^z$ 的本征基矢下的矩阵表示为:
$${\hat{\sigma }}^{+}=\left[\begin{array}{ll}0& 1\\ 0& 0\end{array}\right],{\hat{\sigma }}^{-}=\left[\begin{array}{ll}0& 0\\ 1& 0\end{array}\right],$$

则
$${\hat{\sigma }}^{+}|0⟩=\left[\begin{array}{ll}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{l}0\\ 1\end{array}\right]=\left[\begin{array}{l}1\\ 0\end{array}\right]$$

由上篇博客的学习内容我们知道矩阵积可以写成指标求和的形式，例如 ${\sigma }^{+}\phi \iff {\sum }_j{\sigma }_{ij}^{+}{\phi }_j$，不记得可以戳这张量和线性代数基础，

单体算符及其运算

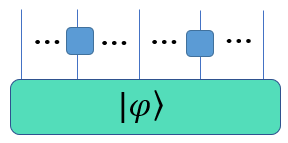
1. 对于N自旋体系，对应希尔伯特空间维数为$2^{\mathrm{N}}$，即量子态的系数为$2^{\mathrm{N}}$维张量，算符的系数为$2^{\mathrm{N}}$×$2^{\mathrm{N}}$维张量。单体算符就是作用到某一个自旋上的算符，例如泡利算符，它的系数维数为2 × 2。如下图，按照上一篇博客所学，每一个腿代表一个指标，每一个指标的维数为2。如果这个时候理解有点困难，我们可以先从最简单的单自旋体系着手，慢慢地向多自旋体系进行过渡。
   

2. 单体算符作用到多体量子态的规则：定义作用在第一个自旋空间的算子 ${\hat{O}}^{(1)}$，易得其对应的系数维数为2×2，三自旋量子态$|\phi ⟩$对应的系数维数为2×2×2。将 ${\hat{O}}^{(1)}$作用到$|\phi ⟩$上：
   $$|{\phi }^{\prime }⟩={\hat{O}}^{(1)}|\phi ⟩={\hat{O}}^{(1)}\otimes {\hat{I}}^{(2)}\otimes {\hat{I}}^{(3)}|\phi ⟩$$
   ${\hat{I}}^{(n)}$为定义在第n个自旋空间的的单位算符。
   注意：对于自旋态，无法定义对某一个自旋的单独操作，相关算符也需要定义在多自旋希尔伯特空间中。

3. 在公式$|{\phi }^{\prime }⟩={\hat{O}}^{(1)}|\phi ⟩={\hat{O}}^{(1)}\otimes {\hat{I}}^{(2)}\otimes {\hat{I}}^{(3)}|\phi ⟩$中，我们可以以指标收缩的方式进行计算。设$|\phi ⟩$和$|{\phi }^{\prime }⟩$的系数分别为三阶张量${\phi }_{ijk}$和$\phi {{}^{\prime }}_{i^{\prime }jk}$，${\hat{O}}^{(1)}$的系数为二阶矩阵${{\hat{O}}_{i^{\prime }i}}^{(1)}$，根据相同指标可以进行收缩我们可以计算：
   $$\phi {{}^{\prime }}_{i^{\prime }jk}=\sum {{\hat{O}}_{i^{\prime }i}}^{(1)}{\phi }_{ijk}$$
   由此我们可以知道，将定义在n个自旋的算符${\hat{O}}^{(n)}$作用到自旋多体态上只需要将算符与第n个指标进行收缩
   注意：虽然只是进行第n个指标进行收缩，实际上所有张量元都会改变。

多体算符及其运算

如果量子算符为幺正算符，那么这些算符构成一个作用在多体态上的大的幺正算符的操作，称之为量子线路。
补充：逆算符等于其转置共轭算符的算符称为幺正算符：$U^{-1}=U^{}{U}^{-1}=U^{+}$

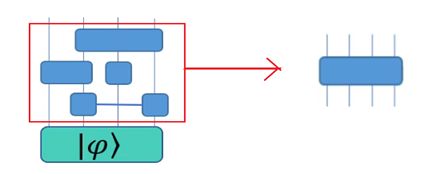
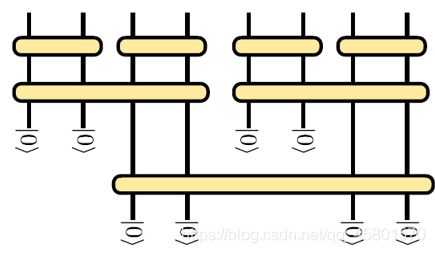
量子线路是可运行于量子计算机的模型，类似于经典计算机上的逻辑门线路。例如下图所示的作用在$|\text{00000000}⟩$上的量子线路，由三个四体量子门和四个二体量子门构成。

对于多体算符，当该算符可以写成多个定义在不同的单体算符的直积时，计算算符作用到多体态上时，由于单体算符作用在不同的空间，互相之间不受干扰，所以算符是相互对易的，所以作用顺序不影响结果，此时仅需要进行多次单体算符的作用即可。例如，将定义在第一和第二个自旋空间中的算符$\hat{O}={\hat{O}}^{(1)}\otimes {\hat{O}}^{(2)}$作用到三自旋态$|\phi ⟩$上，得到量子态$|{\phi }^{\prime }⟩$，相应的系数满足:
$$\phi {{}^{\prime }}_{i^{\prime }{j}^{\prime }k}=\sum _{ij}{O}_{i^{\prime }i}^{(1)}{O}_{j^{\prime }j}^{(2)}{\phi }_{ijk}$$

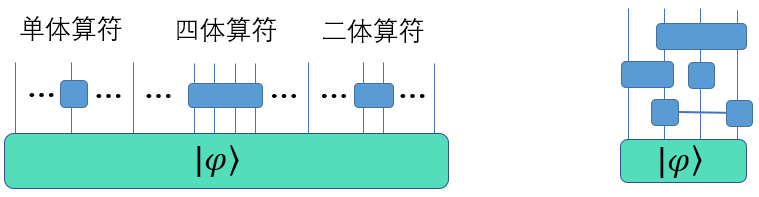
并不是所有的多体算符都可以分解成单体算符的直积。如果算符不能分解成多个单体算符直积的形式，如下图左边所示，则根据分解的情况进行收缩；如果存在不同算符作用在相同自旋上，如下图 右边所示，我们按照上面的规则，由下至上依次将每一层的算符作用到量子态上；也可以先进行算符之间的作用，最后再作用到量子态上。

我是一只正在不断学习、希望早日成为小白的小小白，有什么错误欢迎大家批评指正，喜欢的请点个赞哦！