张量网络算法基础(三、格点模型)
格点模型
- 格点模型
- 1. 热力学基础
- 经典热力学基础
- 量子格点模型的热力学基础
- 2. 海森堡模型的基态计算
- 量子格点模型的基态问题
- 基态计算的退火算法
- 基态计算的严格对角化算法
- 基于自动微分的基态变分算法
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!
格点模型
1. 热力学基础
经典热力学基础
-
对于一个粒子构成的系统,该系统处于某一种状态(记为 s 1 , s 2 , … {{s}_{1}},{{s}_{2,\ldots }} s1,s2,…)的概率 P 由该状态的能量E决定,满足:
P ( s 1 , s 2 , … ; β ) = e − β E ( s 1 , s 2 , … ) Z P({{s}_{1}},{{s}_{2}},\ldots ;\beta )=\frac{{{e}^{-\beta E({{s}_{1}},{{s}_{2}},\ldots )}}}{Z} P(s1,s2,…;β)=Ze−βE(s1,s2,…)
其中 β = 1 / T \beta =1/T β=1/T为倒温度,在机器学习里面叫做超参数 ,Z被称为配分函数,满足:
Z = ∑ s 1 , s 2 , … e − β E ( s 1 , s 2 , … ) Z=\sum\nolimits_{{{s}_{1}},{{s}_{2}},\ldots }{{{e}^{-\beta E({{s}_{1}},{{s}_{2}},\ldots )}}} Z=∑s1,s2,…e−βE(s1,s2,…)
由这个公式可以看出,系统能量越低,处在该状态的概率就越大。 -
热力学量即对应物理量的概率平均值:
O ( β ) = ∑ s 1 , s 2 , … P ( s 1 , s 2 , … ; β ) O ( s 1 , s 2 , … ) O(\beta )=\sum\limits_{{{s}_{1}},{{s}_{2}},\ldots }{P({{s}_{1}},{{s}_{2}},\ldots ;\beta )}O({{s}_{1}},{{s}_{2}},\ldots ) O(β)=s1,s2,…∑P(s1,s2,…;β)O(s1,s2,…)
O ( s 1 , s 2 , … ) O({{s}_{1}},{{s}_{2}},\ldots ) O(s1,s2,…)是在当前状态下对应的观测到的物理量的值。由此可见,建立描述给定物理系统热力学性质的关键在于建立能量 E 和状态 s 1 , s 2 , … {{s}_{1}},{{s}_{2,\ldots }} s1,s2,…之间的函数关系。 -
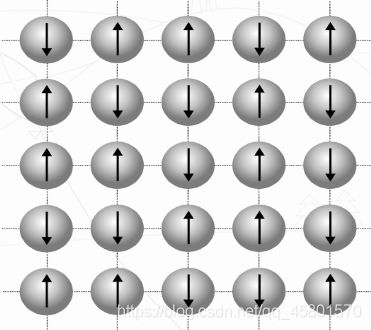
Ising模型由N个Ising自旋构成,如图,每个Ising自旋为图中一个节点,其状态 s i {s}_{i} si可取1或-1。对于给定的状态,其能量满足
E ( s 1 , s 2 , … ) = ∑ ⟨ i , j ⟩ J i j s i s j E({{s}_{1}},{{s}_{2}},\ldots )=\sum\limits_{\left\langle i\left. ,j \right\rangle \right.}{{{J}_{ij}}{{s}_{i}}{{s}_{j}}} E(s1,s2,…)=⟨i,j⟩∑Jijsisj
其中 ⟨ i , j ⟩ \left\langle i \right.\left. ,j \right\rangle ⟨i,j⟩代表图中任意一对相连的Ising自旋, J i j {{J}_{ij}} Jij称为对应连接的耦合系数,也就是自旋之间的相互作用强度。
量子格点模型的热力学基础
-
量子格点模型的热力学基础与经典热力学基础有着极大的相似,量子系统的热力学由有限温密度算子给出:
ρ ^ ( β ) = e − β H ^ / Z \hat{\rho }(\beta )={{e}^{-\beta \hat{H}}}/Z ρ^(β)=e−βH^/Z
其中 H ^ \hat{H} H^为系统哈密顿量,Z为量子配分函数。对于量子系统,给定状态下的能量满足
E ( s 1 , s 2 , . . . ) = ⟨ s 1 s 2 . . . ∣ H ^ ∣ s 1 s 2 . . . ⟩ E({{s}_{1}},{{s}_{2}},...)=\left\langle {{s}_{1}}{{s}_{2}}... \right|\hat{H}\left| {{s}_{1}}{{s}_{2}}... \right\rangle E(s1,s2,...)=⟨s1s2...∣H^∣s1s2...⟩
与经典热力学理论相同,处于 ∣ s 1 , s 2 , . . . ⟩ \left| {{s}_{1}},{{s}_{2}},... \right\rangle ∣s1,s2,...⟩状态下的概率为
P ( s 1 , s 2 , … ; β ) = e − β E ( s 1 , s 2 , … ) Z P({{s}_{1}},{{s}_{2}},\ldots ;\beta )=\frac{{{e}^{-\beta E({{s}_{1}},{{s}_{2}},\ldots )}}}{Z} P(s1,s2,…;β)=Ze−βE(s1,s2,…)
由此可见要建立量子热力学理论关键在于给定哈密顿量,这在后面的学习会体现出来。 -
将能量的表达式 E ( s 1 , s 2 , . . . ) = ⟨ s 1 s 2 . . . ∣ H ^ ∣ s 1 s 2 . . . ⟩ E({{s}_{1}},{{s}_{2}},...)=\left\langle {{s}_{1}}{{s}_{2}}... \right|\hat{H}\left| {{s}_{1}}{{s}_{2}}... \right\rangle E(s1,s2,...)=⟨s1s2...∣H^∣s1s2...⟩代入量子配分函数 Z = ∑ s 1 s 2 , … e − β ⟨ s 1 s 2 ⋯ ∣ H ^ ∣ s 1 s 2 ⋯ ⟩ Z=\sum\nolimits_{{{s}_{1}}{{s}_{2}},\ldots }{{{e}^{-\beta \left\langle {{s}_{1}}{{s}_{2}}\cdots \right|\hat{H}\left| {{s}_{1}}{{s}_{2}}\cdots \right\rangle }}} Z=∑s1s2,…e−β⟨s1s2⋯∣H^∣s1s2⋯⟩
根据基矢的正交完备性 ∑ s 1 s 2 ⋯ ∣ s 1 s 2 ⋯ ⟩ ⟨ s 1 s 2 ⋯ ∣ = I \sum\nolimits_{{{s}_{1}}{{s}_{2}}\cdots }{\left| {{s}_{1}}{{s}_{2}}\cdots \right\rangle }\left\langle {{s}_{1}}{{s}_{2}}\cdots \right|=I ∑s1s2⋯∣s1s2⋯⟩⟨s1s2⋯∣=I,得:
Z = ∑ s 1 s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ e − β H ^ ∣ s 1 s 2 ⋯ ⟩ Z=\sum\nolimits_{{{s}_{1}}{{s}_{2}}\cdots }{\left\langle {{s}_{1}}{{s}_{2}}\cdots \right|{{e}^{-\beta \hat{H}}}\left| {{s}_{1}}{{s}_{2}}\cdots \right\rangle } Z=∑s1s2⋯⟨s1s2⋯∣e−βH^∣s1s2⋯⟩
证明:
已知 e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ ( x → 0 ) e^{x}=1+x+\frac{x^{2}}{2 !}+\frac{x{3}}{3 !}+\cdots(x \rightarrow 0) ex=1+x+2!x2+3!x3+⋯(x→0)
Z = ∑ s s s 2 , … e − β ( s 1 s 2 ⋯ ∣ H ^ ∣ s 1 s 2 ⋯ ) = ∑ s s s 2 , … e ⟨ s 1 s 2 ⋯ ∣ − β H ^ ∣ s 1 s 2 ⋯ ⟩ Z=\sum_{s_{s} s_{2}, \ldots} e^{-\beta\left(s_{1} s_{2} \cdots|\hat{H}|_{s_{1} s_{2}} \cdots\right)}=\sum_{s_{s} s_{2}, \ldots} e^{\left\langle s_{1} s_{2} \cdots|-\beta \hat{H}|_{s_{1} s_{2}} \cdots\right\rangle} Z=∑sss2,…e−β(s1s2⋯∣H^∣s1s2⋯)=∑sss2,…e⟨s1s2⋯∣−βH^∣s1s2⋯⟩
= ∑ s 1 s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ I ∣ s 1 s 2 ⋯ ⟩ + ⟨ s 1 s 2 ⋯ ∣ − β H ^ ∣ s 1 s 2 ⋯ ⟩ + ⟨ s 1 s 2 ⋯ ∣ β 2 H ^ 2 2 ! ∣ s 1 s 2 ⋯ ⟩ + ⋯ =\sum_{s_{1} s_{2} \cdots}\left\langle s_{1} s_{2} \cdots|I| s_{1} s_{2} \cdots\right\rangle+\left\langle s_{1} s_{2} \cdots|-\beta \hat{H}| s_{1} s_{2} \cdots\right\rangle+\left\langle s_{1} s_{2} \cdots\left|\frac{\beta^{2} \hat{H}^{2}}{2 !}\right| s_{1} s_{2} \cdots\right\rangle+\cdots =∑s1s2⋯⟨s1s2⋯∣I∣s1s2⋯⟩+⟨s1s2⋯∣−βH^∣s1s2⋯⟩+⟨s1s2⋯∣∣∣2!β2H^2∣∣∣s1s2⋯⟩+⋯
= ∑ s 1 s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ I − β H ^ + β 2 H ^ 2 2 ! + ⋯ ∣ s 1 s 2 ⋯ ⟩ =\sum_{s_{1} s_{2} \cdots}\left\langle s_{1} s_{2} \cdots\left|I-\beta \hat{H}+\frac{\beta^{2} \hat{H}^{2}}{2 !}+\cdots\right| s_{1} s_{2} \cdots\right\rangle =∑s1s2⋯⟨s1s2⋯∣∣∣I−βH^+2!β2H^2+⋯∣∣∣s1s2⋯⟩
= ∑ s s s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ e − β H ^ ∣ s 1 s 2 ⋯ ⟩ =\sum_{s_{s} s_{2} \cdots}\left\langle s_{1} s_{2} \cdots\left|e^{-\beta \hat{H}}\right| s_{1} s_{2} \cdots\right\rangle =∑sss2⋯⟨s1s2⋯∣∣∣e−βH^∣∣∣s1s2⋯⟩
证毕
又因为 ∣ s 1 , s 2 , . . . ⟩ \left| {{s}_{1}},{{s}_{2}},... \right\rangle ∣s1,s2,...⟩相当于线性代数中的特征向量, ⟨ s 1 s 2 ⋯ ∣ e − β H ^ ∣ s 1 s 2 ⋯ ⟩ \left\langle s_{1} s_{2} \cdots\left|e^{-\beta \hat{H}}\right| s_{1} s_{2} \cdots\right\rangle ⟨s1s2⋯∣∣∣e−βH^∣∣∣s1s2⋯⟩相当于求特征向量对应的特征元素,所以 ∑ s s s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ e − β H ^ ∣ s 1 s 2 ⋯ ⟩ \sum_{s_{s} s_{2} \cdots}\left\langle s_{1} s_{2} \cdots\left|e^{-\beta \hat{H}}\right| s_{1} s_{2} \cdots\right\rangle ∑sss2⋯⟨s1s2⋯∣∣∣e−βH^∣∣∣s1s2⋯⟩对应于求迹的操作即
Z = ∑ s s s 2 ⋯ ⟨ s 1 s 2 ⋯ ∣ e − β H ^ ∣ s 1 s 2 ⋯ ⟩ = Tr ( e − β H ^ ) Z=\sum_{s_{s} s_{2} \cdots}\left\langle s_{1} s_{2} \cdots\left|e^{-\beta \hat{H}}\right| s_{1} s_{2} \cdots\right\rangle=\operatorname{Tr}\left( e^{-\beta \hat{H}}\right) Z=sss2⋯∑⟨s1s2⋯∣∣∣e−βH^∣∣∣s1s2⋯⟩=Tr(e−βH^) -
由上述证明过程我们可以知道算符平均值可以由密度矩阵计算获得:
O ( β ) = ∑ s 1 , s 2 , … P ( s 1 , s 2 , … ; β ) O ( s 1 , s 2 , … ) O(\beta)=\sum_{s_{1}, s_{2}, \ldots} P\left(s_{1}, s_{2}, \ldots ; \beta\right) O\left(s_{1}, s_{2}, \ldots\right) O(β)=∑s1,s2,…P(s1,s2,…;β)O(s1,s2,…)
= ∑ s 1 , s 2 , … e − β E ( s 1 , s 2 , … ) Z ⟨ s 1 s 2 ⋯ ∣ O ^ ∣ s 1 s 2 ⋯ ⟩ =\sum_{s_{1}, s_{2}, \ldots} \frac{e^{-\beta E\left(s_{1}, s_{2}, \ldots\right)}}{Z}\left\langle s_{1} s_{2} \cdots|\hat{O}| s_{1} s_{2} \cdots\right\rangle =∑s1,s2,…Ze−βE(s1,s2,…)⟨s1s2⋯∣O^∣s1s2⋯⟩
= 1 Z ∑ s 1 , s 2 , … ⟨ s 1 s 2 ⋯ ∣ e − β H ^ O ^ ∣ s 1 s 2 ⋯ ⟩ =\frac{1}{Z} \sum_{s_{1}, s_{2}, \ldots}\left\langle s_{1} s_{2} \cdots\left|e^{-\beta \hat{H}} \hat{O}\right| s_{1} s_{2} \cdots\right\rangle =Z1∑s1,s2,…⟨s1s2⋯∣∣∣e−βH^O^∣∣∣s1s2⋯⟩
= Tr ( O ^ e − β H ^ ) / Z =\operatorname{Tr}\left(\hat{O} e^{-\beta \hat{H}}\right) / Z =Tr(O^e−βH^)/Z
补充:一般情况下我们可以认为Z=1,此时Z可省略不写
2. 海森堡模型的基态计算
量子格点模型的基态问题
当系统温度极低时( β = 1 / T \beta =1/T β=1/T), β \beta β 趋于无穷大,系统密度算符由哈密顿量最小的本征态( ∣ g ⟩ \left| g \right\rangle ∣g⟩)给出,称为系统的基态,其对应的本征值 E g {{E}_{g}} Eg称为基态能
H ^ ∣ g ⟩ = E g ∣ g ⟩ \hat{H}\left| g \right\rangle ={{E}_{g}}\left| g \right\rangle H^∣g⟩=Eg∣g⟩
因为哈密顿量最小的本征态对应于密度算符最大的本征态,所以 lim β → ∞ e − β H ^ / Z = ∣ g ⟩ ⟨ g ∣ \underset{\beta \to \infty }{\mathop{\lim }}\,{{e}^{-\beta \hat{H}}}/Z=\left| g \right\rangle \left\langle g \right| β→∞lime−βH^/Z=∣g⟩⟨g∣对应于最大本征值的幂级数求法。
有没有感觉到很懵?怎么就哈密顿量最小的本征态对应于密度算符最大的本征态? lim β → ∞ e − β H ^ / Z = ∣ g ⟩ ⟨ g ∣ \underset{\beta \to \infty }{\mathop{\lim }}\,{{e}^{-\beta \hat{H}}}/Z=\left| g \right\rangle \left\langle g \right| β→∞lime−βH^/Z=∣g⟩⟨g∣ 如何对应于最大本征值的幂级数求法?且听我细细道来。
先回顾一下最大本征值的幂级数算法张量和线性代数基础,先看第一个疑问,我们都知道最大本征值的幂级数算法求的是张量的最大本征值,那么当哈密顿量前面加了个负号,此时求的就是最小本征态 ∣ g ⟩ \left| g \right\rangle ∣g⟩;对于第二个疑问,在 lim β → ∞ e − β H ^ / Z = ∣ g ⟩ ⟨ g ∣ \underset{\beta \to \infty }{\mathop{\lim }}\,{{e}^{-\beta \hat{H}}}/Z=\left| g \right\rangle \left\langle g \right| β→∞lime−βH^/Z=∣g⟩⟨g∣中, β \beta β 趋于无穷大对应于最大本征值的幂级数算法中的 k k k趋于无穷大,哈密顿量即对应已知张量,本征态 ∣ g ⟩ \left| g \right\rangle ∣g⟩对应于最大本征态,基态能 E g {{E}_{g}} Eg对应于最大本征值,这样子解释有没有觉得豁然开朗?

所以基态求解就是求哈密顿量对应矩阵的最小本征态和本征值: E g = min ⟨ g ∣ g ⟩ = 1 ⟨ g ∣ H ^ ∣ g ⟩ {{E}_{g}}=\underset{\left\langle g \right.\left| g \right\rangle =1}{\mathop{\min }}\,\left\langle g \right|\hat{H}\left| g \right\rangle Eg=⟨g∣g⟩=1min⟨g∣H^∣g⟩,找到一个量子态 ∣ g ⟩ \left| g \right\rangle ∣g⟩ 使得在其模等于1的情况下极小化量子态对应的能量,这也是后续学习中一直会用到的一个很重要的思想。
基态计算的退火算法
-
磁场中二自旋的海森堡模型:
H ^ ( h α ) = ∑ α = x , y , z [ s ^ 1 α s ^ 2 α + h α ( s ^ 1 α + s ^ 2 α ) ] \hat{H}({{h}^{\alpha }})=\sum\nolimits_{\alpha =x,y,z}{[{{{\hat{s}}}_{1}}^{\alpha }{{{\hat{s}}}_{2}}^{\alpha }}+{{h}^{\alpha }}({{\hat{s}}_{1}}^{\alpha }+{{\hat{s}}_{2}}^{\alpha })] H^(hα)=∑α=x,y,z[s^1αs^2α+hα(s^1α+s^2α)]
h α {{h}^{\alpha }} hα为沿自旋 α \alpha α方向的外磁场。为了更好的进行理解避免混淆,我们可以写成
H ^ ( h α ) = ∑ α = x , y , z [ s ^ 1 α ⊗ s ^ 2 α + h α ( s ^ 1 α I 2 + I 1 s ^ 2 α ) ] \hat{H}({{h}^{\alpha }})=\sum\nolimits_{\alpha =x,y,z}{[{{{\hat{s}}}_{1}}^{\alpha }\otimes {{{\hat{s}}}_{2}}^{\alpha }}+{{h}^{\alpha }}({{\hat{s}}_{1}}^{\alpha }{{I}_{2}}+{{I}_{1}}{{\hat{s}}_{2}}^{\alpha })] H^(hα)=∑α=x,y,z[s^1α⊗s^2α+hα(s^1αI2+I1s^2α)]
由此易得 H ^ \hat{H} H^的系数是一个4×4矩阵,计算步骤:
(1)获得各个自旋算符的矩阵;
(2)计算 s ^ 1 α s ^ 2 α {{\hat{s}}_{1}}^{\alpha }{{\hat{s}}_{2}}^{\alpha } s^1αs^2α,为4×4矩阵;
(3)计算 s ^ 1 α I 2 , I 1 s ^ 2 α {{\hat{s}}_{1}}^{\alpha }{{I}_{2}},{{I}_{1}}{{\hat{s}}_{2}}^{\alpha } s^1αI2,I1s^2α,为4×4矩阵;
(4)将各项求和获得最终结果。
得到哈密顿量后可对其进行本征值分解,从而得到基态和基态能。
补充: s ^ α = σ ^ α / 2 {{\hat{s}}^{\alpha }}={{\hat{\sigma }}^{\alpha }}/2 s^α=σ^α/2 -
计算基态不一定要获得完整的哈密顿量,例如无外场的海森堡格点模型:
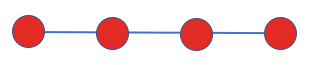
H ^ = ∑ ⟨ i , j ⟩ ∑ α = x , y , z s ^ i α s ^ j α \hat{H}=\sum\nolimits_{\left\langle i \right.,\left. j \right\rangle }{\sum\nolimits_{\alpha =x,y,z}{{{{\hat{s}}}_{i}}^{\alpha }}}{{\hat{s}}_{j}}^{\alpha } H^=∑⟨i,j⟩∑α=x,y,zs^iαs^jα
⟨ i , j ⟩ \left\langle i \right.,\left. j \right\rangle ⟨i,j⟩是图中所有相连的格点对。我们可以先计算第一个和第二个格点之间的哈密顿量,再计算第二个和第三个格点之间的哈密顿量…最后把求得的哈密顿量进行相加就可以获得完整的哈密顿量。
-
基态计算的退火算法:对任意初态 ∣ φ ⟩ \left| \varphi \right\rangle ∣φ⟩进行投影
lim β → ∞ e − β H ^ ∣ φ ⟩ → ∣ g ⟩ \underset{\beta \to \infty }{\mathop{\lim }}\,{{e}^{-\beta \hat{H}}}\left| \varphi \right\rangle \to \left| g \right\rangle β→∞lime−βH^∣φ⟩→∣g⟩
类似于最大幂级数求解法,以4个自旋构成的一维海森堡链退火算法的步骤为例:
(1) 随机初始化量子态 ∣ g 0 ⟩ \left| {{g}_{0}} \right\rangle ∣g0⟩;
(2) 计算 ∣ g ′ t + 1 ⟩ = e − τ H ^ 12 e − τ H ^ 34 ∣ g t ⟩ \left| g{{'}_{t+1}} \right\rangle ={{e}^{-\tau {{{\hat{H}}}_{12}}}}{{e}^{-\tau {{{\hat{H}}}_{34}}}}\left| {{g}_{t}} \right\rangle ∣g′t+1⟩=e−τH^12e−τH^34∣gt⟩并归一化结果;
(3) 计算 ∣ g t + 1 ⟩ = e − τ H ^ 23 ∣ g ′ t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ={{e}^{-\tau {{{\hat{H}}}_{23}}}}\left| g{{'}_{t+1}} \right\rangle ∣gt+1⟩=e−τH^23∣g′t+1⟩并归一化结果;
(4) 检查 ∣ g t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ∣gt+1⟩是否收敛,否则返回步骤(2)

问题来了,首先如何判断 ∣ g t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ∣gt+1⟩是否收敛?只要 ∣ g t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ∣gt+1⟩= ∣ g t ⟩ \left| {{g}_{t}} \right\rangle ∣gt⟩,则 ∣ g t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ∣gt+1⟩收敛。
其次这和最大幂级数求解法有什么关系?
对于算符 A ^ B ^ \hat{A}\hat{B} A^B^
e τ ( A ^ + B ^ ) = e τ A ^ e τ B ^ + τ 2 [ A ^ , B ^ ] + τ 3 [ A ^ , B ^ ] + ⋯ {{e}^{\tau (\hat{A}+\hat{B})}}={{e}^{\tau \hat{A}}}{{e}^{\tau \hat{B}}}+{{\tau }^{2}}[\hat{A},\hat{B}]+{{\tau }^{3}}[\hat{A},\hat{B}]+\cdots eτ(A^+B^)=eτA^eτB^+τ2[A^,B^]+τ3[A^,B^]+⋯
当 A ^ B ^ \hat{A}\hat{B} A^B^对易时
e τ ( A ^ + B ^ ) = e τ A ^ e τ B ^ {{e}^{\tau (\hat{A}+\hat{B})}}={{e}^{\tau \hat{A}}}{{e}^{\tau \hat{B}}} eτ(A^+B^)=eτA^eτB^
当 τ \tau τ为小量时
e τ ( A ^ + B ^ ) − e τ A ^ e τ B ^ = O ( τ 2 ) {{e}^{\tau (\hat{A}+\hat{B})}}-{{e}^{\tau \hat{A}}}{{e}^{\tau \hat{B}}}=O({{\tau }^{2}}) eτ(A^+B^)−eτA^eτB^=O(τ2)
对于上面的4个自旋构成的一维海森堡链,取 τ \tau τ为小量,则
e − τ H ^ ≈ e − τ ( H ^ 12 + H ^ 34 ) e − τ H ^ 23 = e − τ H ^ 12 e − τ H ^ 34 e − τ H ^ 23 {{e}^{-\tau \hat{H}}}\approx {{e}^{-\tau ({{{\hat{H}}}_{12}}+{{{\hat{H}}}_{34}})}}{{e}^{-\tau {{{\hat{H}}}_{23}}}}={{e}^{-\tau {{{\hat{H}}}_{12}}}}{{e}^{-\tau {{{\hat{H}}}_{34}}}}{{e}^{-\tau {{{\hat{H}}}_{23}}}} e−τH^≈e−τ(H^12+H^34)e−τH^23=e−τH^12e−τH^34e−τH^23
上诉步骤作用 k k k次之后,等效倒温度变为 k τ k\tau kτ,由于一维海森堡链退火算法是不断将哈密顿量作用在随机初始化的量子态上,当 k k k足够大时,求得的 ∣ g t + 1 ⟩ \left| {{g}_{t+1}} \right\rangle ∣gt+1⟩就是密度算符的最小本征态,即基态。这就运用了最大幂级数求解的思想。
基态计算的严格对角化算法
严格对角化算法:
(a) 定义线性映射
f ( ∣ φ ⟩ ) : ∣ φ ⟩ → ( I − τ H ^ ) ∣ φ ⟩ = ∣ φ ⟩ − τ ∑ ⟨ i , j ⟩ H ^ i j ∣ φ ⟩ f(\left| \varphi \right\rangle ):\left| \varphi \right\rangle \to (I-\tau \hat{H})\left| \varphi \right\rangle =\left| \varphi \right\rangle -\tau \sum\nolimits_{\left\langle i \right.,\left. j \right\rangle }{{{{\hat{H}}}_{ij}}\left| \varphi \right\rangle } f(∣φ⟩):∣φ⟩→(I−τH^)∣φ⟩=∣φ⟩−τ∑⟨i,j⟩H^ij∣φ⟩
其中 τ \tau τ为小量。
(b) 用迭代算法求解线性映射 f f f的最大本征值和本征态,求出的本征态是哈密顿量最小的本征态( ∣ g ⟩ \left| g \right\rangle ∣g⟩),对应的本征值为 E g {{E}_{g}} Eg。

基于自动微分的基态变分算法
利用自动微分求解是求解对称矩阵的最大本征向量,即求解 max ∣ v ∣ = 1 ∣ v T M v ∣ \underset{\left| v \right|=1}{\mathop{\max }}\,\left| {{v}^{T}}Mv \right| ∣v∣=1max∣∣vTMv∣∣。
定义损失函数
f = − ∣ v T M v ∣ ∣ v 2 ∣ f=-\frac{\left| {{v}^{T}}Mv \right|}{\left| {{v}^{2}} \right|} f=−∣v2∣∣∣vTMv∣∣
则把上述极大化问题转化为损失函数的极小化问题。此时计算 v v v关于 f f f的梯度 d f d v \frac{df}{dv} dvdf,要使得 f f f减小,需要将 v v v沿负梯度方向更新(梯度下降法):
v ← v − η d f d v v\leftarrow v-\eta \frac{df}{dv} v←v−ηdvdf
其中 η \eta η是人为给定的常数,称为更新步长。进行多次迭代更新之后,最终会得到收敛的 v v v,最大本征向量 v ~ \tilde{v} v~与最大本征值 λ \lambda λ满足:
v ~ = v ∣ v ∣ , λ = v ~ T M v \tilde{v}=\frac{v}{\left| v \right|},\lambda ={{\tilde{v}}^{T}}Mv v~=∣v∣v,λ=v~TMv
我是一只正在不断学习、希望早日成为小白的小小白,有什么错误欢迎大家批评指正,喜欢的请点个赞哦!