基于Eigen的多光谱影像主成分分析
title: 基于Eigen的遥感多光谱影像主成分分析
date: 2018-10-03
categories: 遥感图像处理
tags:
主成分分析简介
在多元统计分析中,主成分分析(英语:Principal components analysis,PCA)是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。
计算步骤
输入:n维样本集D=(x(1),x(2),…,x(m)),要降维到的维数n.
输出:降维后的样本集D′
1) 对所有的样本进行中心化:
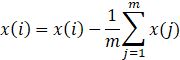
2) 计算样本的协方差矩阵X*XT
3) 对矩阵X*XT进行特征值分解
4)取出最大的n个特征值(从大到小排序)对应的特征向量(w1,w2,…,wn), 将所有的特征向量标准化后,组成特征向量矩阵W。
5)对样本集中的每一个样本x(i),转化为新的样本z(i)=WT*x(i)
6) 得到输出样本集D′=(z(1),z(2),…,z(m)) 即前m成分
博客园有一篇博客详细介绍了PCA 原理
代码实现
主要用到了gdal和Eigen库
gdal用于读写遥感多光谱影像
Eigen则便于各种矩阵运算
#include"gdal_priv.h"
#include"cpl_conv.h" // for CPLMalloc()
#include
#include
#include
#include"Eigen/Dense"
using namespace std;
using namespace Eigen;
//eigen实现主成分分析
void featurenormalize(MatrixXd &X)
{
//计算每一维度均值
MatrixXd meanval = X.colwise().mean();
RowVectorXd meanvecRow = meanval;
//样本均值化为0
X.rowwise() -= meanvecRow;
}
void computeCov(MatrixXd &X, MatrixXd &C)
{
//计算协方差矩阵C = XTX / n-1;
C = X.adjoint() * X;
C = C.array() / (X.rows() - 1);
}
void computeEig(MatrixXd &C, MatrixXd &vec, MatrixXd &val)
{
//计算特征值和特征向量,使用selfadjont按照对阵矩阵的算法去计算,可以让产生的vec和val按照有序排列(默认从大到小)
SelfAdjointEigenSolver eig(C);
vec = eig.eigenvectors();
val = eig.eigenvalues();
}
int computeDim(MatrixXd &val)
{
//输出信息量达到95%的前n主成分
/*int dim;
double sum = 0;
for (int i = val.rows() - 1; i >= 0; --i)
{
sum += val(i, 0);
dim = i;
if (sum / val.sum() >= 0.95)
break;
}
return val.rows() - dim;*/
return 7;//这里设置输出7个主成分
}
void writePcaImg(const char* path, int width, int height, double *pBuff, double *adfGeo, const char *prj, int bandNum, int imageSize, int pcaInd)
{
GDALDriver *pDriver = GetGDALDriverManager()->GetDriverByName("GTiff"); //图像驱动
char** ppszOptions = NULL;
int depth = 8;//图像位深
int dim = 1;//每个图像波段数,这里将每个主成分存储到一个单波段图像
GDALDataset* dst = pDriver->Create(path, width, height, dim, GDT_Float64, ppszOptions);//创建图像
if (dst == nullptr)
printf("Can't Write Image!");
dst->SetGeoTransform(adfGeo);//设置坐标
dst->SetProjection(prj);//设置投影
dst->RasterIO(GF_Write, 0, 0, width, height, &pBuff[(bandNum - pcaInd)*imageSize], width, height,
GDT_Float64, dim, nullptr, dim*depth, width*dim*depth, depth);//写入图像
GDALClose(dst);
}
int main(int argc, char *argv[])
{ //读取影像
char* pszFilename = "D:/gdalData/pca/before.img";
char *outPath = "D:/pca_temp/pca";
GDALDataset *poDataset;
GDALAllRegister();
poDataset = (GDALDataset *)GDALOpen(pszFilename, GA_ReadOnly);
if (poDataset == NULL)
{
printf_s("read failed!\n");
}
else
{
printf_s("read successful!\n");
}
double adfGeoTransform[6];
if (poDataset->GetGeoTransform(adfGeoTransform) == CE_Failure)//读取坐标信息
{
printf("获取参数失败");
}
const char *prj = poDataset->GetProjectionRef();//读取投影信息
int iWidth = poDataset->GetRasterXSize();//图像宽度
int iHeight = poDataset->GetRasterYSize();//图像高度
int iBandCount = poDataset->GetRasterCount();//波段数
int iImageSize = iWidth * iHeight;//图像像元数
double *pBuff1 = new double[iImageSize*iBandCount];//开辟空间存储原始图像
poDataset->RasterIO(GF_Read, 0, 0, iWidth, iHeight, pBuff1,
iWidth, iHeight, GDT_Float64, iBandCount, 0, 0, 0, 0);//读取原始图像
MatrixXd staMat = Map(pBuff1, iImageSize, iBandCount);//将图像读入eigen矩阵
MatrixXd X(iImageSize, iBandCount), C(iBandCount, iBandCount);//按波段存储至X矩阵,构建协方差矩阵C
MatrixXd vec, val;//构建特征向量、特征值矩阵vec、val
X = MatrixXd(staMat);
//零均值化
featurenormalize(X);
//计算协方差
computeCov(X, C);
//计算特征值和特征向量
computeEig(C, vec, val);
//计算损失率,确定降低维数
int dim = computeDim(val);
//计算结果
MatrixXd res = X * vec.rightCols(dim);
//将主成分分量存储至pBuff2
double *pBuff2 = new double[iImageSize*iBandCount];
for (int i = 0; i < dim; ++i)
{
for (int j = 0; j < iImageSize; ++j)
{
pBuff2[i*iImageSize + j] = res(j, i);
}
}
//各个主成分写入图像(包含坐标及投影信息)
for (int i = 0; i < iBandCount; i++)
{
char x[]=" ";
strcpy(x, outPath);
char dstPath[10] = {};
sprintf(dstPath, "%d.tif", i + 1);
strcat(x, dstPath);
writePcaImg(x, iWidth, iHeight, pBuff2, adfGeoTransform, prj, 7, iImageSize, i + 1);
cout << "pca " << i + 1 << " complete" << endl;
}
cout << "pca complete!" << endl;
cin.get();
return 0;
}