一文详解Attention机制
Attention机制
我们知道Seq2Seq模型有一个缺点就是句子太长的话encoder会遗忘,那么decoder接受到的句子特征也就不完全,我们看一下下面这个图,纵轴BLUE是机器翻译的指标,横轴是句子的单词量,我们可以看出用了attention之后模型的性能大大提升。
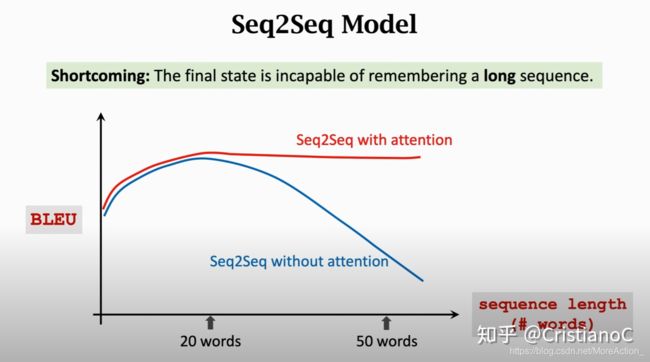
用了注意力机制,Decoder每次更新状态的时候都会再看一遍encoder所有状态,还会告诉decoder要更关注哪部分,这也是attention名字的由来。但是缺点就是计算量很大。

Attention原理
在encoder结束之后,attention和decoder同时工作, 回忆一下,decoder的初始状态 s 0 s_{0} s0 是 encoder最后一个状态, 不同于常规的Seq2Seq, encoder所有状态都要保留,这里需要计算 s 0 s_{0} s0 与每个状态的相关性, 我使用 α i = aligh ( h i , s 0 ) \alpha_{i}=\operatorname{aligh}\left(h_{i}, s_{0}\right) αi=aligh(hi,s0) 这个公式表示计算两者相关性,把结果即为 α i , \alpha_{i}, αi, 记做Weight, encoder有m个状态, 所以一共有m个 α , \alpha, α, 这里所有的值都是介于0和1的实 数, 全部加起来为1。
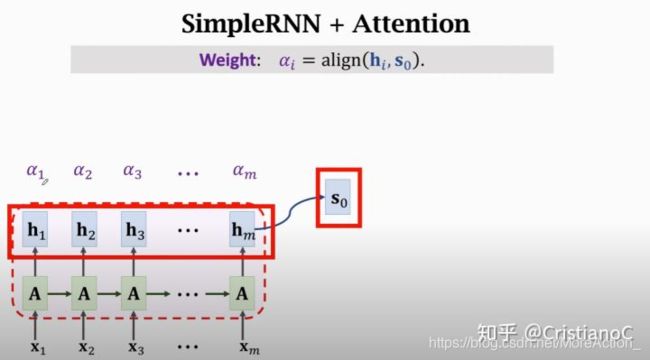
下面看一下怎么计算这个相似性。第一种方法是把 h i h_{i} hi 和 S o S_{o} So 做concat得到更高的向量,然后求矩 阵W与这个向量的乘积, 得到一个向量, 然后再将tanh作用于向量每一个元素,将他压到-1和1之 间,最后计算向量V与刚才计算出来的向量的内积, 这里的向量V和矩阵W都是参数,需要从训练 算出m个 α \alpha α 后,需要对他们做一个softmax变换, 把输出结果记做 α 1 \alpha_{1} α1 到 α m , \alpha_{m}, αm, 因为 是softmax输出,所以他们都大于0相加为1,这是第一篇attention论文提出计算的方法,往后有 很多其他计算的方法,我们来介绍一种更常用的方法。

输入还是 h i h_{i} hi 和 S 0 , S_{0}, S0, 第一步是分别使用两个参数矩阵 W k , W q W_{k}, \quad W_{q} Wk,Wq 做线性变换, 得到 k i k_{i} ki 和 q 0 q_{0} q0 这两 个向量, 这两个参数矩阵要从训练数据中学习。第二步是计算 k i k_{i} ki 与 q 0 q_{0} q0 的内积, 由于有m个K向 量, 所以得到L个 α i \alpha_{i} αi 。第三步就是对这些值做一个softmax变换, α 1 \alpha_{1} α1 到 α m , \alpha_{m}, αm, 因为是softmax输 出,所以他们都大于0相加为1。这种计算方法被Transformer模型采用, Transformer模型是当前 很多nlp问题采用的先进模型。

刚才讲了两种方法来计算 h i h_{i} hi 和 S 0 S_{0} S0 的相关性,现在我们得到了m个相关性 α , \alpha, α, 每个 α \alpha α 对应每个状 态 h i , h_{i}, hi, 有了这些权車 α \alpha α 我们可以对m个状态计算加权平均, 得到一个Context vector C 0 C_{0} C0 。每一 个Context vector都会对应一个decoder状态 s i s_{i} si

接下来我们来看一下decoder是怎么计算新的状态的。我们来回顾一下,假如不用attention,我 们是这样更新状态的,新的状态 S 1 S_{1} S1 是旧状态 S 0 S_{0} S0 与新输入 X 1 X_{1} X1 的函数, 看一下下图左边的公式, 将两者做concat,然后乘上权重矩阵加上偏置b, 最后通过tanh就是我们的新状态,也就是说状态 的更新仅仅是根据上一个状态,并不会看encoder的状态。用attention的话更新状态还要用到我 们计算出的Context vector C 0 , C_{0}, C0, 把三个参数一起做concat后更新。
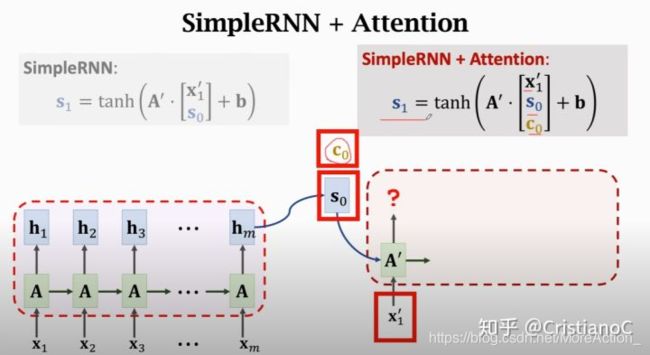
回忆一下, C 0 C_{0} C0 是所有encoder状态 h i h_{i} hi 的加权平均, 所以 C 0 C_{0} C0 知道输入 X 1 X_{1} X1 到 X m X_{m} Xm 的完整信息, decoder新的状态 S 1 S_{1} S1 依赖于 C 0 , C_{0}, C0, 这样RNN遗忘的问题就解决了。下一步则是计算context vector C 1 , C_{1}, C1, 跟之前一样, 先计算权重 α i , \alpha_{i}, αi, 这里是计算 S 1 S_{1} S1 跟之前encoder所有状态的相关性, 得到了m个 α , \alpha, α, 注意一下这里的权重也是要更新的,上一轮算的是跟 s 0 s_{0} s0 的相关性现在算的是跟 S 1 S_{1} S1 的相关性,这样就可以通过加权平均计算出新的 C 1 C_{1} C1 。
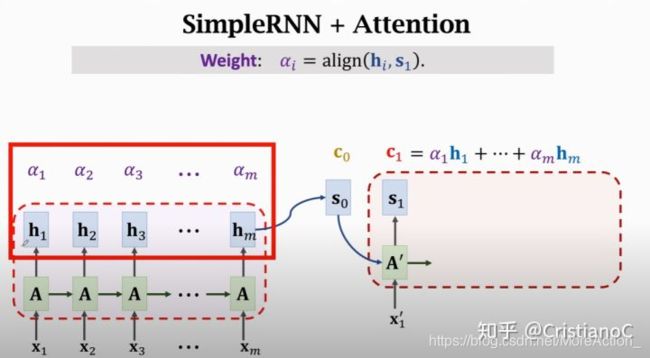
Decoder接受新的输入 X 2 , _{2}, 2, 还是用那个公式计算出新状态, 然后一直循环下去直到结束。
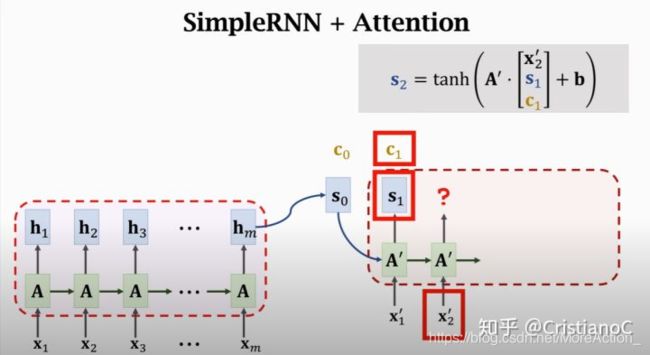
我们知道在这个过程中我们会计算出很多权車 α i , \alpha_{i}, αi, 我们思考一下我们究竟计算了多少个 α \alpha α ?想要 计算出一个context vector C j , C_{j}, Cj, 我们要计算出m个相似性权重 α , \alpha, α, 所以每轮更新都需要计算m个 权重,假如一共有t个state, 那么一共就要计算m\timest个权重, 也就是encoder和decoder数量的乘 积。attention为了不遗忘,代价就是高数量级的计算。

更抽象的理解
简而言之,Attention 机制就是对输入的每个元素考虑不同的权重参数,从而更加关注与输入的元素相似的部分,而抑制其它无用的信息,具体是通过一个叫做attention函数来实现的,它是用来得到attention value的。比较主流的attention框架如下:
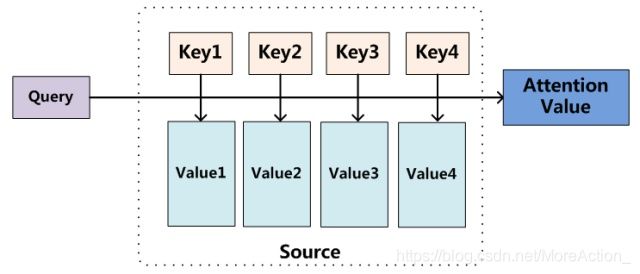
上图其实可以描述出attention value的本质:它其实就是一个查询(query)到一系列键值(key-value)对的映射。
更具体的,也就是attention函数的工作实质,如下图所示:
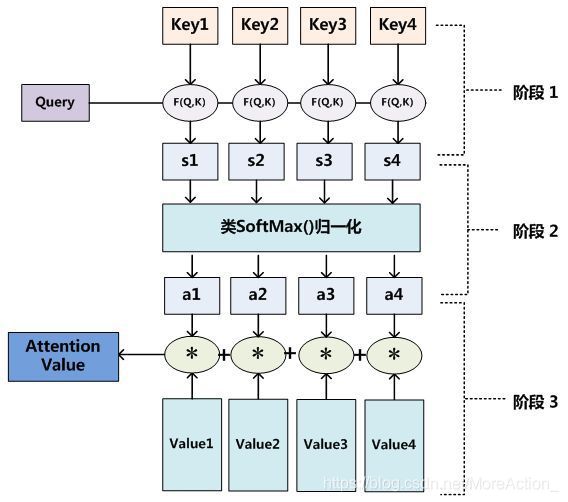
可以看出Attention其实就是把序列中各个元素分配一个权重系数,上面从attention函数是attention机制的工作过程。现在换一个角度来理解,我们将attention机制看做软寻址。就是说序列中每一个元素都由key(地址)和value(元素)数据对存储在存储器里,当有query=key的查询时,需要取出元素的value值(也即query查询的attention值),与传统的寻址不一样,它不是按照地址取出值的,它是通过计算key与query的相似度来完成寻址。这就是所谓的软寻址,它可能会把所有地址(key)的值(value)取出来,上步计算出的相似度决定了取出来值的重要程度,然后按重要程度合并value值得到attention值,此处的合并指的是加权求和。
Attention 的优缺点
优点:
- 一步到位的全局联系捕捉。attention机制可以灵活的捕捉全局和局部的联系,而且是一步到位的。另一方面从attention函数就可以看出来,它先是进行序列的每一个元素与其他元素的对比,在这个过程中每一个元素间的距离都是一,因此它比时间序列RNNs的一步步递推得到长期依赖关系好的多,越长的序列RNNs捕捉长期依赖关系就越弱。
- 并行计算减少模型训练时间。Attention 机制每一步的计算都不依赖于上一步的计算结果,因此可以并行处理。
- 模型复杂度小,参数少
缺点:
缺点很明显,attention机制不是一个"distance-aware"的,它不能捕捉语序顺序(这里是语序哦,就是元素的顺序)。这在NLP中是比较糟糕的,自然语言的语序是包含太多的信息。如果确实了这方面的信息,结果往往会是打折扣的。 当然这个缺点也好搞定,再添加位置信息就好了,所以就有了 position-embedding(位置向量)的概念了,这里就不细说了。
转载来源
https://zhuanlan.zhihu.com/p/135970560
https://zhuanlan.zhihu.com/p/35571412?spm=a2c4e.10696291.0.0.3f4619a49c8SGU
https://www.cnblogs.com/ydcode/p/11038064.html