[cs231n]Assignment1_SVM 代码学习
部分资料来源于网络,仅做个人学习之用
Support Vector Machine
目录
1. Download the CIFAR10 datasets, and load it
2. Preprocessing
3. Define a linear SVM classifier
4. Gradient Check
5. Validation and Test
总结
1. Download the CIFAR10 datasets, and load it
Setup code
Load the CIFAR10 dataset
Show some CIFAR10 images
以上三部分与Knn完全相同:https://blog.csdn.net/Pecony/article/details/104278415
Subsample the data for more efficient code execution
为了更有效地执行代码,对数据进行子采样
knn不具有显示的学习过程,svm分类器则不同,它通过训练学习参数W和 b,将其保存。训练完成,训练数据就可以丢弃,留下学习到的参数即可。之后一个测试图像可以简单地输入函数,并基于计算出的分类分值来进行分类。而参数的学习过程就是训练过程。
KNN与SVM区别:https://blog.csdn.net/Pecony/article/details/104293525
在机器学习中,还有一个必须要重视的问题,那就是过拟合,为了判断是否发生过拟合,我们从训练集中抽取一部分作为验证集,所以我们的数据集就分为了训练集、验证集和测试集
50000个训练集中49000作为训练集,1000作为验证集。测试集只选取10000个测试样本中的前1000个。
"""
我们这里除了训练集、验证集、测试集之外又从训练集中随机选择500个 样本作为development set,在最终的训练和预测之前,我们都使用这个小的数据集, 当然,直接使用完整的训练集也是可以的,不过就是花费的时间有点多。
注意:这里需要先写验证集,再写训练集,否则会报错超出范围!!
"""
# Split the data into train, val, and test sets
num_train = 49000
num_val = 1000
num_test = 1000
# Validation set
mask = range(num_train, num_train + num_val)
X_val = X_train[mask]
y_val = y_train[mask]
# Train set
mask = range(num_train)
X_train = X_train[mask]
y_train = y_train[mask]
# Test set
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)2. Preprocessing
Reshape the images data into rows
将图像数据重新塑成行
# Preprocessing: reshape the images data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print('Train data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)Subtract the mean images
在将我们的数据用于训练和预测之前,我们需要对数据进行归一化处理,这里是对每个特征减去平均值来中心化
中心化是减去均值,标准化是减去均值后除以标准差。
注意:这里减的均值,是训练集的均值,也就是说训练集、验证集、测试集都需要减去前述49000个训练集的均值。
归一化原因:在机器学习领域中,不同评价指标(即特征向量中的不同特征就是所述的不同评价指标)往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果,为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。其中,最典型的就是数据的归一化处理。
归一化目的:使得预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而消除奇怪样本导致的不良影响
# Processing: subtract the mean images
mean_image = np.mean(X_train, axis=0)
plt.figure(figsize=(4,4))
plt.imshow(mean_image.reshape((32,32,3)).astype('uint8'))
plt.show()
X_train -= mean_image
X_val -= mean_image
X_test -= mean_imageAppend the bias dimension of ones
附加1的偏差维度
由下图可知:权重矩阵其实是w和b的,因此我们需要对x增加一个维度。
# append the bias dimension of ones (i.e. bias trick)
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
print('Train data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
# 数据处理完成3. Define a linear SVM classifier
计算loss时利用两层循环进行,对于每一个训练集,利用其乘以W之后,得到其对每个类的得分score以及正确标签的得分correct_class_score, 然后内层循环对每个类,分别计算max(0, score-correct_class_score+1), loss值为输入的所有X的loss之和的均值,然后加上一个L2正则项以防止W过于复杂,即total_loss = avg_loss + lambda * sum(W*W), 后面是我们要实现求dW, 也即求梯度,
对该分类器的构建,主要涉及梯度和损失函数计算、训练和预测模型这两个方面
损失函数的计算的公式如下(这里是加入正则项之后的损失函数值,正则化惩罚可以 带来很多良好的性质):
梯度计算方法如下
class LinearSVM(object):
""" A subclass that uses the Multiclass SVM loss function """
def __init__(self):
self.W = None
"""
以下两个函数的参数相同
输入:
- X:shape(num_train, D)的numpy数组,包含训练数据
由每个维D的num_train样本组成
- y:一个形状的numpy数组(num_train,)包含训练标签,
其中y[i]是X[i]的标签
-reg:float,正则化系数
返回:
-loss:预测值与真实值之间的损耗值
- dW: W的梯度
"""
"""--------------(1)采用数值方式计算损失函数和梯度---------------------------"""
def loss_naive(self, X, y, reg):
# Initialize loss and dW
loss = 0.0
dW = np.zeros(self.W.shape)
# Compute the loss and dW
num_train = X.shape[0]
num_classes = self.W.shape[1]
for i in range(num_train):
scores = np.dot(X[i], self.W)
for j in range(num_classes):
if j == y[i]:
margin = 0
# 当j=y[i]时,代表正确分类,由L=max(...)公式可知正确分类没有loss
else:
margin = scores[j] - scores[y[i]] + 1 # 实现L = max(...) delta = 1
# scores[y[i]]是计算正确分类的分数
if margin > 0:
loss += margin
dW[:,j] += X[i].T
dW[:,y[i]] += -X[i].T
# Divided by num_train
loss /= num_train
dW /= num_train
# Add regularization
loss += 0.5 * reg * np.sum(self.W * self.W)
dW += reg * self.W
return loss, dW
"""--------------(2)采用矩阵的方式计算损失函数和梯度---------------------------"""
def loss_vectorized(self, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i]
- reg: (float) regularization strength
Outputs:
- loss: the loss value between predict value and ground truth
- dW: gradient of W
输入:
- X: shape(num_train, D)的一个numpy阵列,包含训练数据
由每个维D num_train的样本组成
- y: shape(num_train,)的一个numpy阵列,包含训练标签,
y[i]是X[i]的标签
- reg:(float)正则化的strength
输出:
- loss:损失价值之间的预测价值和地面真理
dW:W的梯度
"""
# Initialize loss and dW
loss = 0.0
dW = np.zeros(self.W.shape)
# Compute the loss
num_train = X.shape[0]
scores = np.dot(X, self.W)
correct_score = scores[range(num_train), list(y)].reshape(-1, 1) # delta = -1
margin = np.maximum(0, scores - correct_score + 1)
margin[range(num_train), list(y)] = 0
loss = np.sum(margin) / num_train + 0.5 * reg * np.sum(self.W * self.W)
# Compute the dW
num_classes = self.W.shape[1]
mask = np.zeros((num_train, num_classes))
mask[margin > 0] = 1
mask[range(num_train), list(y)] = 0
mask[range(num_train), list(y)] = -np.sum(mask, axis=1)
dW = np.dot(X.T, mask)
dW = dW / num_train + reg * self.W
return loss, dW
def train(self, X, y, learning_rate = 1e-3, reg = 1e-5, num_iters = 100,
batch_size = 200, print_flag = False):
"""
Train linear SVM classifier 采用随机梯度下降法
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i], y[i] = c, 0 <= c <= C
- learning rate: (float) learning rate for optimization
- reg: (float) regularization strength
- num_iters: 迭代次数(integer) numbers of steps to take when optimization
- batch_size: 批尺寸(integer) number of training examples to use at each step
- print_flag: 为True是显示中间迭代过程(boolean) If true, print the progress during optimization
Outputs:
- loss_history: 每次迭代的损失函数值 A list containing the loss at each training iteration
"""
loss_history = []
num_train = X.shape[0]
dim = X.shape[1]
num_classes = np.max(y) + 1
# Initialize W
if self.W == None:
self.W = 0.001 * np.random.randn(dim, num_classes)
# 迭代和优化
"""
后面是SGD,首先实现train函数,sample的方式也就是一般机器学习里的技巧,利用np.random.choice()生成index,
然后取X,y中的对应项,而更新W的方式更加简单,梯度下降,W = W - lr * dW, 代码如下:
"""
for t in range(num_iters):
idx_batch = np.random.choice(num_train, batch_size, replace=True)
X_batch = X[idx_batch]
y_batch = y[idx_batch]
loss, dW = self.loss_vectorized(X_batch, y_batch, reg)
loss_history.append(loss)
self.W += -learning_rate * dW
if print_flag and t%100 == 0:
print('iteration %d / %d: loss %f' % (t, num_iters, loss))
return loss_history
def predict(self, X):
"""
Use the trained weights of linear SVM to predict data labels
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
Outputs:
- y_pred: A numpy array, predicted labels for the data in X
"""
y_pred = np.zeros(X.shape[0])
scores = np.dot(X, self.W)
y_pred = np.argmax(scores, axis=1)
return y_pred 4. Gradient Check
Define loss function
def loss_naive1(X, y, W, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i]
- W: A numpy array of shape (D, C) contain the weights
- reg: float, regularization strength
Return:
- loss: the loss value between predict value and ground truth
- dW: gradient of W
"""
# Initialize loss and dW
loss = 0.0
dW = np.zeros(W.shape)
# Compute the loss and dW
num_train = X.shape[0]
num_classes = W.shape[1]
for i in range(num_train):
scores = np.dot(X[i], W)
for j in range(num_classes):
if j == y[i]:
margin = 0
else:
margin = scores[j] - scores[y[i]] + 1 # delta = 1
if margin > 0:
loss += margin
dW[:,j] += X[i].T
dW[:,y[i]] += -X[i].T
# Divided by num_train
loss /= num_train
dW /= num_train
# Add regularization
loss += 0.5 * reg * np.sum(W * W)
dW += reg * W
return loss, dW
def loss_vectorized1(X, y, W, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i]
- W: A numpy array of shape (D, C) contain the weights
- reg: (float) regularization strength
Outputs:
- loss: the loss value between predict value and ground truth
- dW: gradient of W
"""
# Initialize loss and dW
loss = 0.0
dW = np.zeros(W.shape)
# Compute the loss
num_train = X.shape[0]
scores = np.dot(X, W)
correct_score = scores[range(num_train), list(y)].reshape(-1, 1) # delta = -1
margin = np.maximum(0, scores - correct_score + 1)
margin[range(num_train), list(y)] = 0
loss = np.sum(margin) / num_train + 0.5 * reg * np.sum(W * W)
# Compute the dW
num_classes = W.shape[1]
mask = np.zeros((num_train, num_classes))
mask[margin > 0] = 1
mask[range(num_train), list(y)] = 0
mask[range(num_train), list(y)] = -np.sum(mask, axis=1)
dW = np.dot(X.T, mask)
dW = dW / num_train + reg * W
return loss, dWGradient check
用公式计算梯度速度很快,唯一不好的就是实现的时候容易出错。为了解决这个问题,在实际操作时常常将分析梯度法的结果和数值梯度法的结果作比较,以此来检查其实现的正确性,这个步骤叫做梯度检查,梯度检验公式如下:
h是一个很小的数字,在实践中近似为1e5
我们这里使用相对误差来比较数值梯度和解析梯度的差,这里放一张cs231n讲义对这里的解释。
以下代码是为了计算我们前面自己计算的梯度和采用数学方法计算的差别
cs231n提供的梯度检验程序:def grad_check_sparse
from gradient_check import grad_check_sparse
import time
# 生成一个随机的小数字SVM权矩阵
W = np.random.randn(3073, 10) * 0.0001
# Without regularization
loss, dW = loss_naive1(X_val, y_val, W, 0)
f = lambda W: loss_naive1(X_val, y_val, W, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, dW)
# With regularization
loss, dW = loss_naive1(X_val, y_val, W, 5e1)
f = lambda W: loss_naive1(X_val, y_val, W, 5e1)[0]
grad_numerical = grad_check_sparse(f, W, dW)loss_naive vs. loss_vectorized
比较两种计算方式
t_st = time.time()
loss_naive, dW_naive = loss_naive1(X_val, y_val, W, 0.00005)
t_ed = time.time()
print('Naive loss: %e computed in %f seconds.' % (loss_naive, t_ed - t_st))
t_st = time.time()
loss_vectorized, dW_vectorized = loss_vectorized1(X_val, y_val, W, 0.00005)
t_ed = time.time()
print('Vectorized loss: %e computed in %f seconds.' % (loss_vectorized, t_ed - t_st))
diff_loss = loss_naive - loss_vectorized
diff_dW = np.linalg.norm(dW_naive - dW_vectorized, ord='fro')
print('Difference of loss: %f' % diff_loss)
print('Difference of dW: %f' % diff_dW)由上图可知,两种计算方式得到的损失函数值是相同的,而采用向量方法计算时间花费少很多,因此接下来将使用 svm_loss_vectorized (矩阵)方法计算损失函 数和梯度。
既然两种方法计算得出的损失函数值是一样的,那么梯度应该也是一样的,也就不需要再对第二种方法进行梯度检验了,不过损失函 数是一维的,而梯度是二维的,可以使用 np.linalg.norm 函数来计算范数,其余同 上。
因此,确定了损失函数和梯度的计算方式。
Stochastic Gradient Descent
随机梯度下降法
现在已知采用向量方法计算损失函数和梯度效率最高,并且得到的梯度经验证误差很小,接下来我们将使用随机梯度下降法(SGD)来进行梯度更新, 使得损失函数值最小。
svm = LinearSVM()
loss_history = svm.train(X_train, y_train, learning_rate = 1e-7, reg = 2.5e4, num_iters = 2000,
batch_size = 200, print_flag = True)可视化损失函数的值:
# Plot the loss_history
plt.plot(loss_history)
plt.xlabel('Iteration number')
plt.ylabel('Loss value')
plt.show()通过该图,我们看到损失函数值在越来越小,已经在发生收敛。
训练完成之后,将参数保存,我们接下来就可以使用这些参数进行预测,并计算准确率,代码如下
# Use svm to predict
# Training set
y_pred = svm.predict(X_train)
num_correct = np.sum(y_pred == y_train)
accuracy = np.mean(y_pred == y_train)
print('Training correct %d/%d: The accuracy is %f' % (num_correct, X_train.shape[0], accuracy))
# Test set
y_pred = svm.predict(X_test)
num_correct = np.sum(y_pred == y_test)
accuracy = np.mean(y_pred == y_test)
print('Test correct %d/%d: The accuracy is %f' % (num_correct, X_test.shape[0], accuracy))5. Validation and Test
Cross-validation
学习速率和正则项是超参数
通过手动调整超参数,可以让模型收敛的更快。接下来通过交叉验证来选择较好的学习率和正则项系数。
从列举的学习率和正则项中选择验证集正确率最高的超参数,将参数 保存到 best_svm 中,其中 results 存储的是形如 {(lr,reg): (train_accuracy,val_accuracy)} 的字典。
learning_rates = [1.4e-7, 1.5e-7, 1.6e-7]
regularization_strengths = [8000.0, 9000.0, 10000.0, 11000.0, 18000.0, 19000.0, 20000.0, 21000.0]
results = {}
best_lr = None
best_reg = None
best_val = -1 # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.
for lr in learning_rates:
for reg in regularization_strengths:
svm = LinearSVM()
loss_history = svm.train(X_train, y_train, learning_rate = lr, reg = reg, num_iters = 2000)
y_train_pred = svm.predict(X_train)
accuracy_train = np.mean(y_train_pred == y_train)
y_val_pred = svm.predict(X_val)
accuracy_val = np.mean(y_val_pred == y_val)
if accuracy_val > best_val:
best_lr = lr
best_reg = reg
best_val = accuracy_val
best_svm = svm
results[(lr, reg)] = accuracy_train, accuracy_val
print('lr: %e reg: %e train accuracy: %f val accuracy: %f' %
(lr, reg, results[(lr, reg)][0], results[(lr, reg)][1]))
print('Best validation accuracy during cross-validation:\nlr = %e, reg = %e, best_val = %f' %
(best_lr, best_reg, best_val)) 也可以将上述结果可视化,面积的大小代表正确率的大小
# Visualize the cross-validation results
import math
x_scatter = [math.log10(x[0]) for x in results]
y_scatter = [math.log10(x[1]) for x in results]
# Plot training accuracy
plt.figure(figsize=(10,10))
make_size = 100
colors = [results[x][0] for x in results] # 使用面积来表示正确率的大小
plt.subplot(2, 1, 1)
plt.scatter(x_scatter, y_scatter, make_size, c = colors)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('Training accuracy')
# Plot validation accuracy
colors = [results[x][1] for x in results]
plt.subplot(2, 1, 2)
plt.scatter(x_scatter, y_scatter, make_size, c = colors)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('Validation accuracy')
plt.show()Test
使用刚刚保存的最好的模型来进行预测,并输出预测的准确率
# Use the best svm to test
y_test_pred = best_svm.predict(X_test)
num_correct = np.sum(y_test_pred == y_test)
accuracy = np.mean(y_test_pred == y_test)
print('Test correct %d/%d: The accuracy is %f' % (num_correct, X_test.shape[0], accuracy))Visualize the weights for each class
通过可视化下权重,看看模型到底在学习什么东西。
W = best_svm.W[:-1, :] # delete the bias 将偏置分离出来,也就是说,我们只可视化权重。
W = W.reshape(32, 32, 3, 10)
W_min, W_max = np.min(W), np.max(W)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
plt.subplot(2, 5, i+1)
imgW = 255.0 * ((W[:, :, :, i].squeeze() - W_min) / (W_max - W_min))
plt.imshow(imgW.astype('uint8'))
plt.axis('off')
plt.title(classes[i])
plt.show()权重可视化的结果,比如car这一类,可以隐约看到汽车的轮廓,权重参数学习到了这些图像的特征。
总结
1. 完成一个使用向量方法计算svm损失函数;
2. 完成一个使用向量方法来分析梯度;
3. 使用数学方法来检查梯度
4. 用验证集来微调学习率和正则项;
5. 使用随机梯度下降法来优化损失函数;
6. 可视化最后学习到的权重
![[cs231n]Assignment1_SVM 代码学习_第1张图片](http://img.e-com-net.com/image/info8/a54c931613fa4a41b3ec1acf3612a38d.jpg)
![[cs231n]Assignment1_SVM 代码学习_第2张图片](http://img.e-com-net.com/image/info8/3ce20f4aa5414c7ba28c77b54ca27db9.jpg)



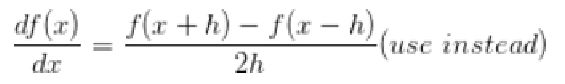
![[cs231n]Assignment1_SVM 代码学习_第3张图片](http://img.e-com-net.com/image/info8/47a9ad64d91c47f5be448a1842151cf2.jpg)
![[cs231n]Assignment1_SVM 代码学习_第4张图片](http://img.e-com-net.com/image/info8/7ca0db2bbcbd488db6099a4cdcdbbc87.png)
![[cs231n]Assignment1_SVM 代码学习_第5张图片](http://img.e-com-net.com/image/info8/02f949f5e7e44e15842da194c6ba64da.jpg)