Python词性标注HMM+viterbi实现
文章目录
- 一些理论
- 概率图模型
- 贝叶斯网络
- 马尔科夫模型
- 隐马尔科夫模型
- HMM应用之——隐序列解码(词性标注)
- 1、基础配置、数据预处理
- 2、HMM参数训练
- 3、频数 --> 概率对数
- 隐→显 发射矩阵
- 初始隐态矩阵
- 隐态转移矩阵
- 4、维特比算法
- 节点最大概率矩阵
- 节点转移记录矩阵
- 隐态序列标号
- 5、标注结果打印
- 附录
一些理论
概率图模型
利用图来表示与模型有关的变量的联合概率分布
贝叶斯网络
将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个网络。
如果该网络是有向无环图,则这个网络称为贝叶斯网络。
p ( A , B , C , D ) = P ( A ) P ( B ∣ A ) P ( C ∣ A , B ) P ( D ∣ C ) p(A,B,C,D)=P(A)P(B|A)P(C|A,B)P(D|C) p(A,B,C,D)=P(A)P(B∣A)P(C∣A,B)P(D∣C)
马尔科夫模型
若贝叶斯网络退化成线性链,则得到马尔科夫模型。
已知 n n n 个有序随机变量,根据贝叶斯定理,其联合分布可写成条件分布的连乘
p ( x 1 , x 2 , . . . x n ) = ∏ i = 1 n p ( x i ∣ x i − 1 , . . . x 1 ) p(x_1,x_2,...x_n) = \prod_{i=1}^n p(x_i|x_{i-1},...x_1) p(x1,x2,...xn)=i=1∏np(xi∣xi−1,...x1)
马尔科夫模型是指,假设序列中的任一随机变量只与它的前 1 1 1 个变量有关,与更早的变量条件独立
p ( x i ∣ x i − 1 , . . . x 1 ) = p ( x i ∣ x i − 1 ) p(x_i|x_{i-1},...x_1) = p(x_i|x_{i-1}) p(xi∣xi−1,...x1)=p(xi∣xi−1)
在此假设下,其联合分布可简化为
p ( x 1 , x 2 , . . . x n ) = p ( x 1 ) ∏ i = 2 n p ( x i ∣ x i − 1 ) p(x_1,x_2,...x_n) = p(x_1) \prod_{i=2}^n p(x_i|x_{i-1}) p(x1,x2,...xn)=p(x1)i=2∏np(xi∣xi−1)
为了表达当前变量与更早的变量之间的关系,可引入高阶马尔科夫性,指当前随机变量与它的前 m m m 个变量有关
p ( x 1 , x 2 , . . . x n ) = ∏ i = 1 n p ( x i ∣ x i − 1 , . . . x i − m ) p(x_1,x_2,...x_n) = \prod_{i=1}^n p(x_i|x_{i-1},...x_{i-m}) p(x1,x2,...xn)=i=1∏np(xi∣xi−1,...xi−m)
隐马尔科夫模型
对于离散型随机变量
显性序列: X = x 1 , x 2 , . . . x n X=x_1,x_2,...x_n X=x1,x2,...xn
隐性序列: Z = z 1 , z 2 , . . . z n Z=z_1,z_2,...z_n Z=z1,z2,...zn

显性序列 X X X 已知,求解最大概率的隐性序列 Z Z Z ,即是最大化 p ( Z ∣ X ) p(Z|X) p(Z∣X)
p ( Z ∣ X ) = p ( X ∣ Z ) p ( Z ) = p ( x 1 , x 2 , . . . x n ∣ z 1 , z 2 , . . . z n ) p ( z 1 , z 2 , . . . z n ) p(Z|X)=p(X|Z)p(Z)= p(x_1,x_2,...x_n|z_1,z_2,...z_n) p(z_1,z_2,...z_n) p(Z∣X)=p(X∣Z)p(Z)=p(x1,x2,...xn∣z1,z2,...zn)p(z1,z2,...zn)
根据马尔科夫假设,任一随机变量只与它的前 1 1 1 个变量有关
p ( x 1 , x 2 , . . . x n ∣ z 1 , z 2 , . . . z n ) = ∏ i = 1 n p ( x i ∣ z i ) p(x_1,x_2,...x_n|z_1,z_2,...z_n)=\prod_{i=1}^np(x_i|z_i) p(x1,x2,...xn∣z1,z2,...zn)=i=1∏np(xi∣zi)
p ( z 1 , z 2 , . . . z n ) = p ( z 1 ) ∏ i = 2 n p ( z i ∣ z i − 1 ) p(z_1,z_2,...z_n) = p(z_1) \prod_{i=2}^n p(z_i|z_{i-1}) p(z1,z2,...zn)=p(z1)i=2∏np(zi∣zi−1)
模型简化为3个部分
- (隐态→显态)发射概率模型: ∏ i = 1 n p ( x i ∣ z i ) \prod_{i=1}^np(x_i|z_i) ∏i=1np(xi∣zi)
- (隐态)初始概率模型: p ( z 1 ) p(z_1) p(z1)
- (隐态)转移概率模型: ∏ i = 2 n p ( z i ∣ z i − 1 ) \prod_{i=2}^n p(z_i|z_{i-1}) ∏i=2np(zi∣zi−1)
HMM应用之——隐序列解码(词性标注)
1、基础配置、数据预处理
import numpy as np, pandas as pd
START = 'start' # 句始tag
END = 'end' # 句末tag
NOUN = 'subj' # 名词
ADV = 'adv' # 副词
ADJ = 'adj' # 形容词
corpus = np.array([
('我', NOUN), ('很', ADV), ('菜', ADJ), ('。', END),
('我', NOUN), ('好', ADV), ('菜', ADJ), ('。', END),
('我', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('他', NOUN), ('很', ADV), ('菜', ADJ), ('。', END),
('他', NOUN), ('好', ADV), ('菜', ADJ), ('。', END),
('他', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('菜', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('我', NOUN), ('菜', ADJ), ('。', END),
('我', NOUN), ('好', ADJ), ('。', END),
('他', NOUN), ('菜', ADJ), ('。', END),
('他', NOUN), ('好', ADJ), ('。', END),
('菜', NOUN), ('好', ADJ), ('。', END),
('我', NOUN), ('好', ADV), ('好', ADJ), ('。', END),
('他', NOUN), ('好', ADV), ('好', ADJ), ('。', END),
], dtype=str)
words = sorted(set(corpus[:, 0]))
tags = sorted(set(corpus[:, 1]))
W = len(words) # 词汇量
T = len(tags) # 词性种类数
word2id = {words[i]: i for i in range(W)}
tag2id = {tags[i]: i for i in range(T)}
id2tag = {i: tags[i] for i in range(T)}
2、HMM参数训练
SMOOTHNESS = 1e-8 # 平滑参数
emit_p = np.zeros((T, W)) + SMOOTHNESS # emission_probability
start_p = np.zeros(T) + SMOOTHNESS # start_probability
trans_p = np.zeros((T, T)) + SMOOTHNESS # transition_probability
prev_tag = START # 前一个tag
for word, tag in corpus:
wid, tid = word2id[word], tag2id[tag]
emit_p[tid][wid] += 1
if prev_tag == START:
start_p[tid] += 1
else:
trans_p[tag2id[prev_tag]][tid] += 1
prev_tag = START if tag == END else tag # 句尾判断
3、频数 --> 概率对数
取对数,防止下溢,乘法运算转换成更简单的加法运算
∑ i = 1 n ln p ( x i ∣ z i ) + ln p ( z 1 ) + ∑ i = 2 n ln p ( z i ∣ z i − 1 ) \sum_{i=1}^n \ln p(x_i|z_i) + \ln p(z_1) + \sum_{i=2}^n \ln p(z_i|z_{i-1}) i=1∑nlnp(xi∣zi)+lnp(z1)+i=2∑nlnp(zi∣zi−1)
start_p = np.log(start_p / sum(start_p))
for i in range(T):
emit_p[i] = np.log(emit_p[i] / sum(emit_p[i]))
trans_p[i] = np.log(trans_p[i] / sum(trans_p[i]))
隐→显 发射矩阵
pd.DataFrame(emit_p, tags, words)
初始隐态矩阵
pd.DataFrame(start_p.reshape(1, T), ['START'], tags)
隐态转移矩阵
pd.DataFrame(trans_p, tags, tags)
4、维特比算法
sentence = list('菜好好')
obs = [word2id[w] for w in sentence] # 观测序列
le = len(obs) # 序列长度
# 动态规划矩阵
dp = np.array([[-1e99] * T] * le) # 节点最大概率对数
path = np.zeros((le, T), dtype=int) # 节点转移记录
for j in range(T):
dp[0][j] = start_p[j] + emit_p[j][obs[0]]
path[0][j] = -1
for i in range(1, le):
for j in range(T):
dp[i][j], path[i][j] = max(
(dp[i - 1][k] + trans_p[k][j] + emit_p[j][obs[i]], k)
for k in range(T))
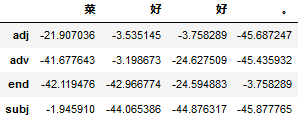
节点最大概率矩阵
pd.DataFrame(dp.T, tags, sentence)
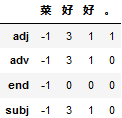
节点转移记录矩阵
pd.DataFrame(path.T, tags, sentence)
隐态序列标号
states = [np.argmax(dp[le - 1])]
# 从后到前的循环来依次求出每个单词的词性
for i in range(le - 2, -1, -1):
states.insert(0, path[i + 1][states[0]])
5、标注结果打印
for word, tid in zip(sentence, states):
print(word, id2tag[tid])
菜 subj
好 adv
好 adj
。 end
附录
语料地址:
https://github.com/AryeYellow/PyProjects/blob/master/NLP/Viterbi-词性标注/POS_tagging.ipynb
GitHub地址:
https://github.com/AryeYellow/PyProjects/blob/master/NLP/Viterbi-词性标注/HMM.ipynb
注释
| en | cn |
|---|---|
| Probabilistic Graphical Model | 概率图模型 |
| Bayesian Network | 贝叶斯网络 |
| Directed Acyclic Graph | 有向无环图 |
| HMM | Hidden Markov Model |
| part-of-speech tagging | 词性标注 |
| observation | n. 观察 |
| emission | n. 发射 |
| transition | n. 过渡;转变 |
| dynamic programming | 动态规划 |
完整代码
import numpy as np
"""配置"""
SMOOTHNESS = 1e-8
START = 'start' # 句始tag
END = 'end' # 句末tag
NOUN = 'subj' # 名词
ADV = 'adv' # 副词
ADJ = 'adj' # 形容词
"""数据预处理"""
corpus = np.array([
('我', NOUN), ('很', ADV), ('菜', ADJ), ('。', END),
('我', NOUN), ('好', ADV), ('菜', ADJ), ('。', END),
('我', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('他', NOUN), ('很', ADV), ('菜', ADJ), ('。', END),
('他', NOUN), ('好', ADV), ('菜', ADJ), ('。', END),
('他', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('菜', NOUN), ('很', ADV), ('好', ADJ), ('。', END),
('我', NOUN), ('菜', ADJ), ('。', END),
('我', NOUN), ('好', ADJ), ('。', END),
('他', NOUN), ('菜', ADJ), ('。', END),
('他', NOUN), ('好', ADJ), ('。', END),
('菜', NOUN), ('好', ADJ), ('。', END),
('我', NOUN), ('好', ADV), ('好', ADJ), ('。', END),
('他', NOUN), ('好', ADV), ('好', ADJ), ('。', END),
], dtype=str)
words = sorted(set(corpus[:, 0]))
tags = sorted(set(corpus[:, 1]))
W = len(words) # 词汇量
T = len(tags) # 词性种类数
word2id = {words[i]: i for i in range(W)}
tag2id = {tags[i]: i for i in range(T)}
id2tag = {i: tags[i] for i in range(T)}
"""HMM训练"""
emit_p = np.zeros((T, W)) + SMOOTHNESS # emission_probability
start_p = np.zeros(T) + SMOOTHNESS # start_probability
trans_p = np.zeros((T, T)) + SMOOTHNESS # transition_probability
prev_tag = START # 前一个tag
for word, tag in corpus:
wid, tid = word2id[word], tag2id[tag]
emit_p[tid][wid] += 1
if prev_tag == START:
start_p[tid] += 1
else:
trans_p[tag2id[prev_tag]][tid] += 1
prev_tag = START if tag == END else tag # 句尾判断
# 频数 --> 概率对数
start_p = np.log(start_p / sum(start_p))
for i in range(T):
emit_p[i] = np.log(emit_p[i] / sum(emit_p[i]))
trans_p[i] = np.log(trans_p[i] / sum(trans_p[i]))
def viterbi(sentence):
"""维特比算法"""
obs = [word2id[w] for w in sentence.strip()] # 观测序列
le = len(obs) # 序列长度
# 动态规划矩阵
dp = np.zeros((le, T)) # 记录节点最大概率对数
path = np.zeros((le, T), dtype=int) # 记录上个转移节点
for j in range(T):
dp[0][j] = start_p[j] + emit_p[j][obs[0]]
for i in range(1, le):
for j in range(T):
dp[i][j], path[i][j] = max(
(dp[i - 1][k] + trans_p[k][j] + emit_p[j][obs[i]], k)
for k in range(T))
# 隐序列
states = [np.argmax(dp[le - 1])]
# 从后到前的循环来依次求出每个单词的词性
for i in range(le - 2, -1, -1):
states.insert(0, path[i + 1][states[0]])
# 打印
for word, tid in zip(sentence, states):
print(word, id2tag[tid])
"""测试"""
x = '菜好好。'
viterbi(x)
补充:马尔科夫网络、马尔科夫模型、马尔科夫过程、贝叶斯网络的区别
- 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个网络。
- 如果该网络是有向无环图,则这个网络称为
贝叶斯网络。 - 如果这个图退化成线性链的方式,则得到
马尔科夫模型;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是马尔科夫过程。 - 若上述网络是无向的,则是无向图模型,又称
马尔科夫随机场。 - 如果在给定某些条件的前提下,研究这个马尔科夫随机场,则得到
条件随机场。 - 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到
线性链条件随机场。