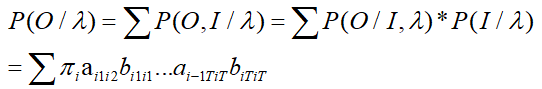基于HMM的中文分词
一、前言
本文主要是基于隐马尔科夫模型对中文词进行分词。
二、HMM的理解
HMM是一个统计模型,主要有HMM由初始状态概率分布π、状态转移概率分布A以及观测概率分布B确定,为了方便表达,把A, B, π 用 λ 表示,即:
λ = (A, B, π)
状态集合S:{B,M,E,S},N=4
π:初始状态概率分布,如{B:-0.26268660809250016, E:-3.14e+100, M:-3.14e+100, S:-1.4652633398537678}
A:状态转移概率分布,N*N的矩阵如:{'S': {'S': 747969.0, 'E': 0.0, 'M': 0.0, 'B': 563988.0}, 'E': {'S': 737404.0, 'E': 0.0, 'M': 0.0, 'B': 651128.0}
B:观测概率分布或者称为发射概率分布,隐藏状态到观测状态的混淆矩阵,M*N,如{'S': {'否': 10.0, '昔': 25.0, '直': 238.0, '六': 1004.0, '殖': 17.0, '仗': 36.0, '挪': 15.0, '朗': 151.0}}
O:输出序列
需理解什么是隐藏状态和可见状态,隐藏状态从一个隐藏状态到下一个隐藏状态;可见状态是一个隐藏状态到可见状态的输出。
A、HMM有两个假设
1、假设任意时刻t的状态只依赖于前一个时刻的状态,与其他时刻的状态和观测序列无关
2、假设任意时刻的观测只依赖与该市可的马尔科夫的状态,与其他观测,状态无关。
B、HMM常见的解决三个问题
1、已知λ和观测序列O = {o1,o2, ..., oT},对观测序列的概率进行计算,即计算模型 λ 下观测序列O出现的概率P(O | λ),是一种概率计算问题,常用前向-后向算法(关心概率和的问题);
2 ![]() 、根据观测序列,参数λ求解,是一种学习问题,非监督学习算法,常用EM算法;
、根据观测序列,参数λ求解,是一种学习问题,非监督学习算法,常用EM算法;
3、已知λ观测序列O = {o1,o2, ..., oT},对隐藏状态的最大序列进行预测,即计算给定观测序列条件概率P(I|O, λ )最大的状态序列I,是一种预测/解码问题,监督学习算法,常用维特比算法,如中文分词(关心最大概率问题);
C、HMM的概率计算问题算法的推导
问题:已知HMM的参数 λ,和观测序列O = {o1, o2, ...,oT},求P(O|λ)
思路:列举所有可能状态长度为T的序列集合I={i1,i2,…,iT},求解各个状态序列与观测状态的联合概率P(O,I|λ),最后求解所有可能的状态序列求和∑P(O,I|λ)得到P(O|λ);
算法推导:
P(O,I|λ) = P(O|I,λ)*P(I|λ)
P(O|I,λ) 即对固定状态下,观测状态为O的概率:
对于P(I|λ),
P(I|λ) = p(i1,i2,i3…iT|λ)
= p(i1|λ)*p(i2|i1,λ)*p(i3…iT|λ)
= P(i1 |λ)*P(i2 | i1, λ)*P(i3 | i2, λ)...P(iT | iT-1, λ)
最终得到
但这个的时间复杂度是相当大的,因此提出了前向-后向算法(动态规划中的一个方法)进行改进,这儿不做详述。
对于第三个问题,也就是本文所要进行的分词算法,只是将目标问题变成了从求和变成了求最大化的问题,因此利用了动态规划中的维特比算法,不做详述。
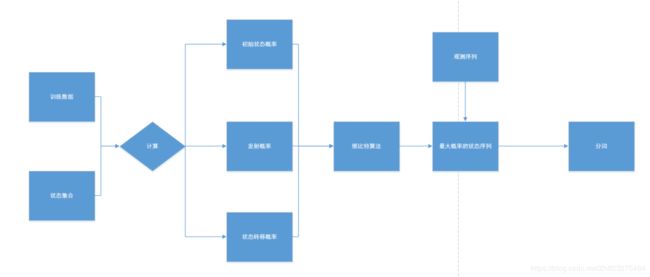
三、构建结构
四、分词的技术路线
五、实验
5.1 根据语料进行训练
class HmmTrain:
def __init__(self):
self.line_index = -1
self.char_set = set()
def int(self):# 初始化字典
trans_dic = {}# 存储状态转移矩阵
emit_dict = {} # 发射概率(状态->词语的条件概率)
Count_dict = {} # 存储所有状态序列,用于归一化分母
start_dict = {} # 存储状态的初始概率
state_list = ['B','M','E','S']
for state in state_list:
trans_dic[state] = {}
for state1 in state_list:
trans_dic[state][state1] = 0.0
for state in state_list:
start_dict[state] = 0.0
emit_dict[state] = {}
Count_dict[state] = 0
return trans_dic, emit_dict, start_dict, Count_dict
'''保存模型'''
def save_model(self,word_dict,model_path):
f = open(model_path, 'w')
f.write(str(word_dict))
f.close()
'''词语状态转换'''
def get_word_status(self,word): # 根据词语,输出词语对应的SBME状态
'''
S:单字词
B:词的开头
M:词的中间
E:词的末尾
'''
word_status = []
if len(word) == 1:
word_status.append('S')
elif len(word) == 2:
word_status = ['B', 'E']
else:
M_num = len(word) - 2
M_list = ['M'] * M_num
word_status.append('B')
word_status.extend(M_list)
word_status.append('E')
return word_status
'''基于人工标注语料库,训练发射概率,初始窗台,转移概率'''
def train(self, train_filepath, trans_path, emit_path, start_path):
trans_dict, emit_dict, start_dict, Count_dict = self.int()
for line in open(train_filepath):
self.line_index +=1
line = line.strip()
if not line:
continue
char_list = []
for i in range(len(line)):
if line[i] == " ":
continue
char_list.append(line[i])
self.char_set = set(char_list) # 训练语料库中所有字的集和
word_list = line.split(" ")
line_status = [] # 统计状态序列
for word in word_list:
line_status.extend(self.get_word_status(word))
if len(char_list) == len(line_status):
for i in range(len(line_status)):
if i == 0: #如果只有一个词,则直接算作是初始概率
start_dict[line_status[0]] += 1 # start_dict 记录句子第一个字的状态,用于计算初始状态概率
Count_dict[line_status[0]] += 1 # 记录每一个状态的出现次数
else: # 统计上一个状态到下一个状态,两个状态之间的转移概率
trans_dict[line_status[i-1]][line_status[i]] += 1
Count_dict[line_status[i]] += 1
# 统计发射概率
if char_list[i] not in emit_dict[line_status[i]]:
emit_dict[line_status[i]][char_list[i]] = 0.0
else:
emit_dict[line_status[i]][char_list[i]] += 1 # 用于计算发射概率
else:
continue
# 进行归一化
for key in start_dict: # 状态的初始概率
start_dict[key] = start_dict[key] *1.0 / self.line_index
for key in trans_dict: # 状态转移概率
for key1 in trans_dict[key]:
trans_dict[key][key1] = trans_dict[key][key1] / Count_dict[key]
for key in emit_dict: # 发射概率(状态->词语的条件概率)
for word in emit_dict[key]:
emit_dict[key][word] = emit_dict[key][word] /Count_dict[key]
self.save_model(trans_dict,trans_path)
self.save_model(emit_dict,emit_path)
self.save_model(start_dict,start_path)
return trans_dict,emit_dict,start_dict
5.2 对训练的语料进行预测
class HmmCut:
def __init__(self):
trans_path = './model/prob_trans.model'
emit_path = './model/prob_emit.model'
start_path = './model/prob_start.model'
self.prob_trans = self.load_model(trans_path)
self.prob_emit = self.load_model(emit_path)
self.prob_start = self.load_model(start_path)
'''加载模型'''
def load_model(self, model_path):
f = open(model_path, 'r')
a = f.read()
word_dict = eval(a)
f.close()
return word_dict
'''verterbi算法求解'''
def viterbi(self, obs, states, start_p, trans_p, emit_p): # 维特比算法(一种递归算法)
V = [{}]
path = {}
for y in states:
V[0][y] = start_p[y] * emit_p[y].get(obs[0], 0) # 在位置0,以y状态为末尾的状态序列的最大概率
path[y] = [y]
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
state_path = ([(V[t - 1][y0] * trans_p[y0].get(y, 0) * emit_p[y].get(obs[t], 0), y0) for y0 in states if V[t - 1][y0] > 0])
if state_path == []:
(prob, state) = (0.0, 'S')
else:
(prob, state) = max(state_path)
V[t][y] = prob
newpath[y] = path[state] + [y]
path = newpath # 记录状态序列
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states]) # 在最后一个位置,以y状态为末尾的状态序列的最大概率
return (prob, path[state]) # 返回概率和状态序列
# 分词主控函数
def cut(self, sent):
prob, pos_list = self.viterbi(sent, ('B', 'M', 'E', 'S'), self.prob_start, self.prob_trans, self.prob_emit)
seglist = list()
word = list()
for index in range(len(pos_list)):
if pos_list[index] == 'S':
word.append(sent[index])
seglist.append(word)
word = []
elif pos_list[index] in ['B', 'M']:
word.append(sent[index])
elif pos_list[index] == 'E':
word.append(sent[index])
seglist.append(word)
word = []
seglist = [''.join(tmp) for tmp in seglist]
return seglist六、总结
本文主要是对hmm应用于中文分词进行知识归纳和理解,其思想可以用来对以后实际中遇到的问题进行一个思维模式的借鉴,其主要为对自己所学知识进行整理,用于记录自己所学的感悟。
七、参考资料
1、http://www.cnblogs.com/sddai/p/8475424.html
2、https://blog.csdn.net/continueoo/article/details/77893587
3、https://www.cnblogs.com/skyme/p/4651331.html
4、https://github.com/liuhuanyong/WordSegment/