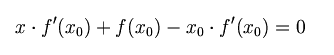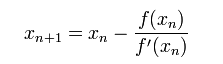2月20 牛顿法，海赛矩阵（hesse matrix），作用求根与最优化，与梯度（平面拟合局部）相比效率高，因为用二次曲面去拟合局部

1.0牛顿法（牛顿法又被很形象地称为是"切线法"）

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。https://www.cnblogs.com/shixiangwan/p/7532830.html ； https://zhuanlan.zhihu.com/p/92359902

一般来说，牛顿法主要应用在两个方面，1：求方程的根；2：最优化。

1.1求方程的根；

求方程的根主要是泰勒展开的前两项,一阶展开

具体步骤：
　　首先，选择一个接近函数 f (x)零点的 x0，计算相应的 f (x0) 和切线斜率f ’ (x0)（这里f ’ 表示函数 f 的导数）。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标，也就是求如下方程的解：

我们将新求得的点的 x 坐标命名为x1，通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

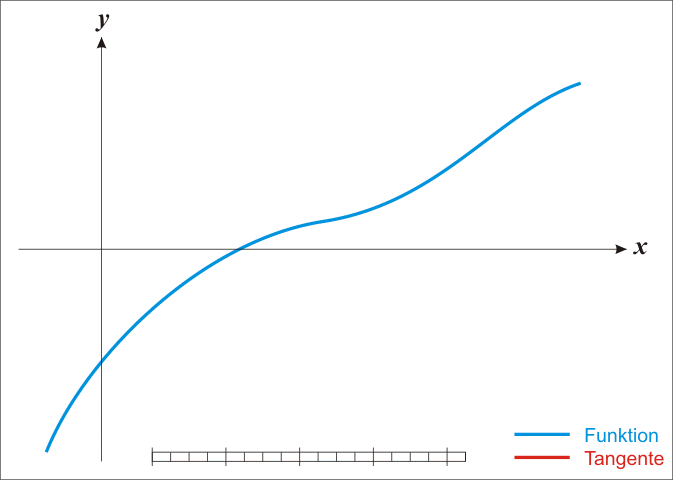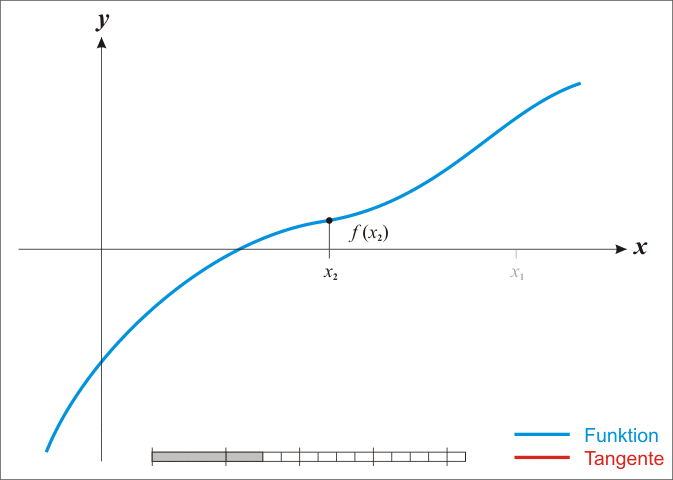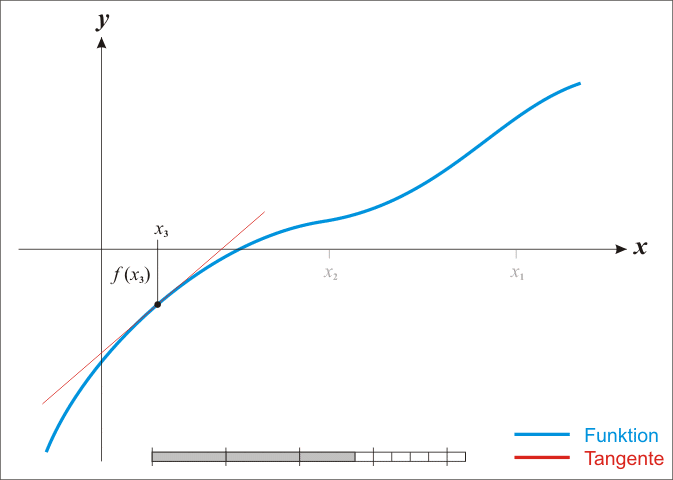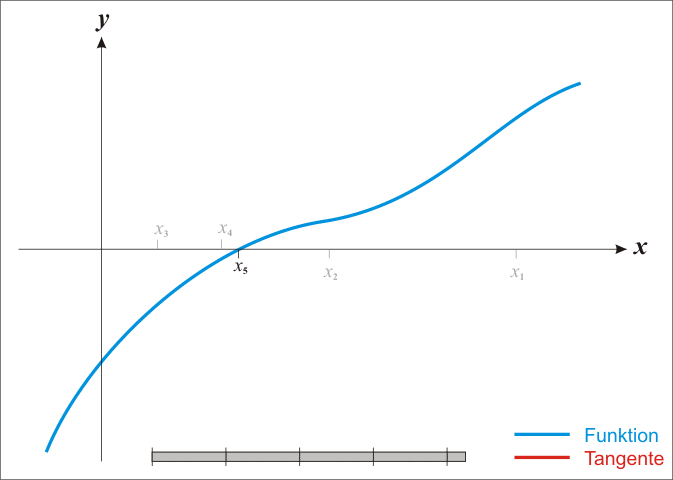
已经证明，如果f ’ 是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。 并且，如果f ’ (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。

由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径（二维情况）如下图所示：

补充：海赛矩阵（hesse matrix）

https://blog.csdn.net/u014688145/article/details/53688585【算法细节系列（3）：梯度下降法，牛顿法，拟牛顿法】

对于高维函数，用牛顿法求极值也是这个形式，只不过这里的$f^{\prime \prime }(x)$和$f^{\prime }(x)$都变成了矩阵和向量。而且你也可以想到，高维函数二阶导有多个，写成矩阵的形式就是这样

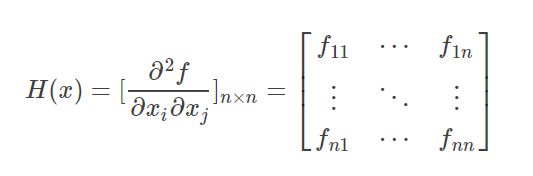
所以有了海赛矩阵，牛顿迭代法就有如下形式：

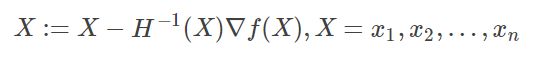
对于H(x)有如下结论：
如果H(x)是正定矩阵，则临界点M处是一个局部的极小值。
如果H(x)是负定矩阵，则临界点M处是一个局部的极大值。
如果H(x)是不定矩阵，则临界点M处不是极值。

1.2最优化

参考：https://zhuanlan.zhihu.com/p/37524275

最优化，主要是二阶泰勒展开

算法演示

参考： https://blog.csdn.net/Big_Pai/article/details/88540037

代码

import random
import numpy as np
import matplotlib.pyplot as plt
 
def dampnm(fun,gfun,hess,x0):
    # 用牛顿法求解无约束问题
    #x0是初始点，fun，gfun和hess分别是目标函数值，梯度，海森矩阵的函数
    maxk = 500
    rho = 0.55
    sigma = 0.4
    k = 0
    epsilon = 1e-5
    
    f=open("牛顿.txt","w")
    W = np.zeros((2, 20000))
 
    while k < maxk:
        W[:, k] = x0
        gk = gfun(x0)
        Gk = hess(x0)
        dk = -1.0*np.linalg.solve(Gk,gk)
        print(k, np.linalg.norm(dk))
        f.write(str(k)+'   '+str(np.linalg.norm(gk))+"\n")
        if np.linalg.norm(dk) < epsilon:
            break
 
        x0 += dk
        k += 1
    W = W[:, 0:k + 1]  # 记录迭代点
    return x0,fun(x0),k,W
 
# 函数表达式fun
fun = lambda x:100*(x[0]**2-x[1])**2 + (x[0]-1)**2
 
# 梯度向量 gfun
gfun = lambda x:np.array([400*x[0]*(x[0]**2-x[1])+2*(x[0]-1), -200*(x[0]**2-x[1])])
 
# 海森矩阵 hess
hess = lambda x:np.array([[1200*x[0]**2-400*x[1]+2, -400*x[0]],[-400*x[0],200]])
 
if __name__=="__main__":
    X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)
    X2 = np.arange(-3.5, 2 + 0.05, 0.05)
    [x1, x2] = np.meshgrid(X1, X2)
    f = 100 * (x2 - x1 ** 2) ** 2 + (1 - x1) ** 2  # 给定的函数
    plt.contour(x1, x2, f, 20)  # 画出函数的20条轮廓线
 
    x0 = np.array([-1.2, 1])
    out=dampnm(fun, gfun, hess, x0)
    print(out[2],out[0])
 
    W = out[3]
    print(W[:,:])

    plt.plot(W[0, :], W[1, :], 'g*-')
    plt.show()

np.array的各类用法：

a = np.array([2,23,4])  # list 1d
print(a)
# [2 23 4]

a = np.arange(10,20,2) # 10-19 的数据，2步长
"""
array([10, 12, 14, 16, 18])
"""

a = np.zeros((3,4)) # 数据全为0，3行4列
"""
array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.]])
"""

https://morvanzhou.github.io/tutorials/data-manipulation/np-pd/2-2-np-array/

牛顿法也是求解无约束最优化问题的常用方法，有收敛速度快的优点。牛顿法是迭代算法，每一步需要求解目标函数的海赛矩阵的逆矩阵。同时还有拟牛顿法、阻尼牛顿法、修正牛顿法 等等。

1.4牛顿法和梯度下降法的比较

1.牛顿法：
是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。
收敛速度很快。
海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

2.梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。
越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡.

梯度下降法和牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法是用二阶的海森矩阵的逆矩阵求解。相对而言，使用牛顿法收敛更快（迭代更少次数）。但是每次迭代的时间比梯度下降法长

如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。
参考：https://zhuanlan.zhihu.com/p/37524275

至于为什么牛顿法收敛更快，通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。更多的可见：最优化问题中，https://www.zhihu.com/question/19723347 牛顿法为什么比梯度下降法求解需要的迭代次数更少？

关于牛顿法和梯度下降法的效率对比：

从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步 ，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面 ，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

梯度法和牛顿法有如下区别：
https://zhuanlan.zhihu.com/p/78185057

梯度下降法是一阶优化算法，牛顿法是二阶优化算法
牛顿法的收敛速度相比梯度下降法常常较快，但是计算开销大，实际中常用拟牛顿法
牛顿法对初始值有一定要求，在非凸优化问题中（如神经网络训练），牛顿法很容易陷入鞍点（牛顿法步长会越来越小），而梯度下降法则很容易逃离鞍点（因此在神经网络训练中一般使用梯度下降法，高维空间的神经网络中存在大量鞍点）正是因为梯度法不如牛顿法准确，这种随机性使得梯度法比牛顿法容易逃离.
梯度下降法在靠近最优点时会震荡，因此步长调整在梯度下降法中是必要的，具体有adagrad, adadelta, rmsprop, adam等一系列自适应学习率的方法