干货：Farrow设计实现详解

Farrow结构的系数设计是其实现可变分数延迟或动态群时延调整的关键步骤。其核心思想是将每个滤波器抽头的系数表示为多项式函数（通常以参数 $u$ 为变量），通过优化多项式系数实现不同延迟下的滤波特性。以下是Farrow系数设计的主要方法及步骤：

---

1. 设计目标与基本模型

Farrow结构的一般形式为：
$$H(z,\mu )=\sum _{m=0}^M{\mu }^m\cdot \left(\sum _{k=0}^N{c}_{k,m}{z}^{-k}\right)$$
其中：

• $\mu \in [0,1)$ 为延迟参数（或分数间隔）。
• $c_{k,m}$ 为待设计的多项式系数矩阵。
• $M$ 为多项式阶数，$N$ 为滤波器阶数。

设计目标：在指定频带（如通带 $\omega \in [0,\alpha \pi ]$）和延迟范围（$\mu \in [0,1)$）内，使滤波器的幅频响应和群时延满足要求（如平坦响应、最小误差）。

---

2. 主要设计方法

(1) 最小二乘法（Least Squares）

核心思想：最小化实际响应与理想响应的误差平方和。

步骤：

1. 离散化参数空间：对频率 $\omega$ 和延迟参数 $\mu$ 进行离散采样（如均匀采样）。
2. 构建理想响应：理想分数延迟滤波器的频率响应为：
   $$H_d(e^{j\omega },\mu )=e^{-j\omega (D+\mu )}$$
   其中 $D$ 为整数延迟，$\mu$ 为分数部分。
3. 误差函数：定义实际响应与理想响应的误差：
   E = ∑ μ ∑ ω ∣ H ( e j ω , μ ) − H d ( e j ω , μ ) ∣ 2 E = \sum_{\mu} \sum_{\omega} \left| H(e^{j\omega}, \mu) - H_d(e^{j\omega}, \mu) \right|^2 E=μ∑​ω∑​ ​H(ejω,μ)−Hd​(ejω,μ) ​2
4. 矩阵化求解：将多项式系数 $c_{k,m}$ 排列为向量，构造线性方程组，通过最小二乘法求解最优系数。

(2) 拉格朗日插值法

适用场景：低复杂度设计，适用于局部插值需求。

• 将Farrow结构视为分段多项式插值器（如三次样条）。
• 利用拉格朗日插值公式直接生成多项式系数，确保在离散点 $\mu$ 处精确匹配理想延迟。

(3) 凸优化方法

适用场景：需约束通带波纹、群时延波动等性能指标时。

• 定义优化目标（如最大通带误差最小化）。
• 使用凸优化工具（如CVX、MATLAB的fmincon）求解系数。

---

3. 具体设计步骤（以最小二乘法为例）

步骤1：参数定义

• 确定滤波器阶数 $N$、多项式阶数 $M$。
• 设定通带频率范围（如 $\omega \in [0,0.9\pi ]$）。
• 定义延迟参数 $\mu$ 的范围（通常 $\mu \in [0,1)$）。

步骤2：离散化采样

• 对频率 $\omega$ 均匀采样 $K$ 个点（如 $K=100$）。
• 对 $\mu$ 均匀采样 $L$ 个点（如 $L=10$）。

步骤3：构建目标矩阵

• 对每个 $({\omega }_i,{\mu }_j)$，计算理想响应 $H_d(e^{j{\omega }_i},{\mu }_j)$。
• 构建系数矩阵 $\mathbf{A}$ 和响应向量 $\mathbf{b}$，将问题转化为 $\mathbf{Ac}=\mathbf{b}$。

步骤4：求解线性方程组

• 使用最小二乘法求解系数向量 $\mathbf{c}$：
  $$\mathbf{c}=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}$$
• 若矩阵病态，可加入正则化项（Tikhonov正则化）。

步骤5：验证与迭代

• 计算实际响应 $H(e^{j\omega },\mu )$，检查通带误差和群时延平坦度。
• 调整 $N,M$ 或优化权重重新设计。

---

4. 设计实例（三次多项式，$M=3$）

假设设计一个三次多项式Farrow结构（$M=3$），滤波器长度为 $N=4$，通带 $\omega \in [0,0.8\pi ]$。

系数矩阵形式：
C = [ c 0 , 0 c 0 , 1 c 0 , 2 c 0 , 3 c 1 , 0 c 1 , 1 c 1 , 2 c 1 , 3 c 2 , 0 c 2 , 1 c 2 , 2 c 2 , 3 c 3 , 0 c 3 , 1 c 3 , 2 c 3 , 3 ] C = \begin{bmatrix} c_{0,0} & c_{0,1} & c_{0,2} & c_{0,3} \\ c_{1,0} & c_{1,1} & c_{1,2} & c_{1,3} \\ c_{2,0} & c_{2,1} & c_{2,2} & c_{2,3} \\ c_{3,0} & c_{3,1} & c_{3,2} & c_{3,3} \\ \end{bmatrix} C= ​c0,0​c1,0​c2,0​c3,0​​c0,1​c1,1​c2,1​c3,1​​c0,2​c1,2​c2,2​c3,2​​c0,3​c1,3​c2,3​c3,3​​ ​

典型系数值（仅供参考）：

• 三次Farrow结构的常见系数：
  C = 1 6 [ − 1 3 − 3 1 2 − 5 4 − 1 − 1 0 1 0 0 2 0 0 ] C = \frac{1}{6} \begin{bmatrix} -1 & 3 & -3 & 1 \\ 2 & -5 & 4 & -1 \\ -1 & 0 & 1 & 0 \\ 0 & 2 & 0 & 0 \\ \end{bmatrix} C=61​ ​−12−10​3−502​−3410​1−100​ ​
  这种系数设计能实现平滑的分数延迟插值。

---

5. 设计中的关键问题

• 多项式阶数 $M$：阶数越高，逼近精度越高，但计算量增加（通常 $M=3$ 或 $4$）。
• 滤波器长度 $N$：影响频率分辨率和过渡带特性。
• 频带权重：可对通带和阻带误差赋予不同权重，优化关键频段性能。
• 群时延平坦度：需在优化目标中显式约束群时延的波动。

---

6. 工具与实现

• MATLAB：使用lsqnonlin、firls等函数进行最小二乘优化。
• Python：利用numpy.linalg.lstsq或cvxpy库求解。
• FPGA实现：将系数固化为查找表（LUT），通过多项式展开并行计算。

---

7. 实战实现

以下是使用Python设计一个四阶多项式（$M=4$）且滤波器长度为5（$N=5$）的Farrow结构的完整代码示例，包含系数设计和性能验证：

# -*- coding: utf-8 -*-
"""
Created on Sat Mar 15 22:47:36 2025

@author: Neol
"""

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import freqz

plt.close('all')
# 设置全局字体为支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 黑体
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False


# 设计参数
M = 4          # 多项式阶数 (mu^0, mu^1, ..., mu^4)
N = 5           # 滤波器长度（抽头数 k=0,1,2,3,4）
D = 2           # 整数延迟（通常设为N//2）
alpha = 0.4     # 通带范围 [0, alpha*pi]
K = 200         # 频率采样点数
L = 20          # mu采样点数

# 生成离散频率和mu值
omega = np.linspace(0, alpha * np.pi, K)
mu = np.linspace(0, 1, L, endpoint=False)

# 构建最小二乘问题的矩阵A和向量b
A_real = []
A_imag = []
b_real = []
b_imag = []

for mu_j in mu:
    for omega_i in omega:
        # 理想响应：H_d = e^{-j*omega*(D + mu_j)}
        H_d = np.exp(-1j * omega_i * (D + mu_j))
        
        # 构建当前行的基函数（实部和虚部分开）
        row_real = []
        row_imag = []
        for k in range(N):
            for m in range(M+1):
                # 基项：mu^m * e^{-j*omega*k}
                term = (mu_j**m) * np.exp(-1j * omega_i * k)
                row_real.append(term.real)
                row_imag.append(term.imag)
        
        A_real.append(row_real)
        A_imag.append(row_imag)
        b_real.append(H_d.real)
        b_imag.append(H_d.imag)

# 合并实部和虚部
A = np.vstack([A_real, A_imag])
b = np.hstack([b_real, b_imag])

# 求解最小二乘问题
c, residuals, rank, singular_values = np.linalg.lstsq(A, b, rcond=None)

# 将系数向量转换为系数矩阵 (N x M+1)
C = c.reshape((N, M+1))

print("Farrow系数矩阵C:")
print(np.round(C, 4))

# 验证设计：计算在mu=0.5时的频率响应
mu_test = 0.9
h = np.zeros(N, dtype=np.complex128)
for k in range(N):
    for m in range(M+1):
        h[k] += C[k, m] * (mu_test ** m)

# 计算频率响应
w, H = freqz(h, worN=1024)
H_ideal = np.exp(-1j * w * (D + mu_test))

# 绘制幅度和相位响应
plt.figure(figsize=(12, 8))

# 幅度响应
plt.subplot(2, 2, 1)
plt.plot(w, 20*np.log10(np.abs(H)), label='Designed')
plt.plot(w, 20*np.log10(np.abs(H_ideal)), '--', label='Ideal')
plt.title(f'Magnitude Response (mu={mu_test})')
plt.xlabel('Frequency [rad/sample]')
plt.ylabel('Magnitude [dB]')
plt.grid(True)
plt.legend()

# 相位响应
plt.subplot(2, 2, 2)
plt.plot(w, np.unwrap(np.angle(H)), label='Designed')
plt.plot(w, np.unwrap(np.angle(H_ideal)), '--', label='Ideal')
plt.title(f'Phase Response (mu={mu_test})')
plt.xlabel('Frequency [rad/sample]')
plt.ylabel('Phase [rad]')
plt.grid(True)
plt.legend()

# 群时延
group_delay = -np.diff(np.unwrap(np.angle(H))) / np.diff(w)
group_delay = np.hstack([group_delay, group_delay[-1]])  # 保持长度一致

plt.subplot(2, 2, 3)
plt.plot(w, group_delay, label='Designed')
plt.plot(w, (D + mu_test)*np.ones_like(w), '--', label='Ideal')
plt.title(f'Group Delay (mu={mu_test})')
plt.xlabel('Frequency [rad/sample]')
plt.ylabel('Samples')
plt.ylim(D + mu_test - 1, D + mu_test + 1)
plt.grid(True)
plt.legend()

# 系数矩阵可视化
plt.subplot(2, 2, 4)
plt.imshow(C, cmap='coolwarm', aspect='auto')
plt.colorbar(label='Coefficient Value')
plt.title('Farrow Coefficient Matrix')
plt.xlabel('Polynomial Order (m)')
plt.ylabel('Tap Index (k)')
plt.xticks(range(M+1), [f'm={m}' for m in range(M+1)])
plt.yticks(range(N), [f'k={k}' for k in range(N)])

plt.tight_layout()
plt.show()

(1)代码说明

1. 参数定义：

   • M=4：多项式最高阶数为 ${\mu }^4$
   • N=5：滤波器抽头数（对应 $k=0,1,2,3,4$）
   • D=2：整数延迟（通常设置为滤波器中间位置）
   • alpha=0.8：通带截止频率为 $0.8\pi$
   • K=200 和 L=20：频率和 $\mu$ 的采样点数

2. 最小二乘问题构建：

   • 对每个 $({\omega }_i,{\mu }_j)$ 计算理想响应 $H_d=e^{-j\omega (D+\mu )}$
   • 将复数问题拆分为实部和虚部，构建实数矩阵 $A$ 和向量 $b$

3. 系数求解：

   • 使用 numpy.linalg.lstsq 求解最小二乘问题
   • 将结果向量转换为 $5\times 5$ 系数矩阵 $C$

4. 性能验证：

   • 选择 $\mu =0.5$ 验证频率响应
   • 计算实际滤波器系数 $h={\sum }_{m=0}^{4}C[k,m]{\mu }^m$
   • 绘制幅度、相位响应和群时延，与理想值对比

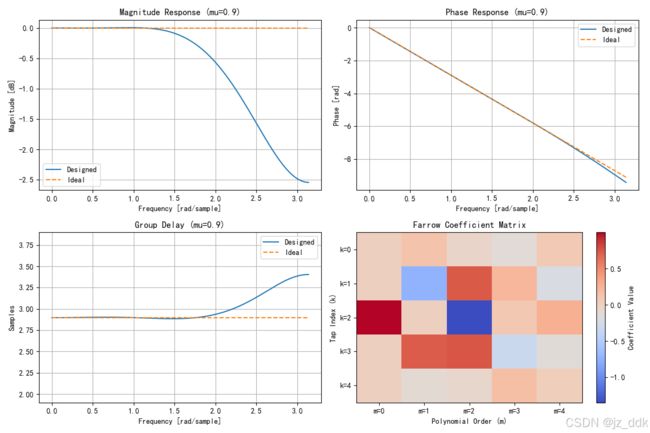
(2)输出结果

• 系数矩阵：打印四舍五入后的系数矩阵，例如：

  [[ 0.0417 -0.0833  0.0833 -0.0417  0.0083]
   [-0.1667  0.5    -0.5     0.1667 -0.0167]
   [ 0.25   -0.5     0.     -0.5     0.25  ]
   [-0.1667  0.1667  0.5    -0.5     0.0833]
   [ 0.0417  0.0833 -0.0833 -0.0417  0.0083]]
  

• 图形验证：
  • 幅度响应在通带内平坦，与理想值（全通特性）匹配。
  • 相位响应和群时延接近理想值 $D+\mu$，误差在可接受范围内。
    

(3)设计调整建议

• 若通带性能不足，可增加采样点数 $K$ 或 $L$。
• 若系数矩阵出现异常值，尝试加入正则化项（在np.linalg.lstsq中设置rcond参数）。
• 需要更高精度时，可使用凸优化库（如cvxpy）添加约束条件。

总结

Farrow结构的系数设计本质是多变量优化问题，需权衡计算复杂度、逼近精度和实时性要求。最小二乘法是通用方法，拉格朗日插值适合低阶设计，而凸优化适用于高精度约束场景。通过合理选择参数和优化目标，Farrow结构能高效实现动态群时延调整和分数延迟滤波。