混淆矩阵,准确率,精确率,召回率,Roc曲线
参考了统计学习方法,概率论与数理统计,工程线性代数,西瓜书,Machine Learnig with python做的总结,所以不能作为教程,还包含自己用sklearn做的一些对比实验,原文是写在jupyter上的,这里是直接转为.md导过来的,所以格式有些问题,有些东西还待完善…
(一)machine learning terminology
分类器(Classifier)
一段程序或一个函数将无标签实例映射到类别,则成称这段程序或这个函数为分类器
混淆矩阵(Confusion Matrix)
用来观察分类器的性能,其中矩阵列标表示实例的预测类别,行标表示实例的真是类别.下图就是一个二分类(binary classification)的混淆矩阵.表示正确预测男性42人,正确预测女性32人,18人被误分类为男性,8人被误分类为女性.
准确率 (accuracy(error rate))
准确率表示为: 正 确 预 测 实 例 数 / 实 例 总 数 正确预测实例数/实例总数 正确预测实例数/实例总数.上例中准确率是 ( 42 + 32 ) / ( 42 + 32 + 8 + 18 ) = 0.72 (42+32)/(42+32+8+18)=0.72 (42+32)/(42+32+8+18)=0.72
准确性悖论(Accuracy paradox)
我们假设有如下一个混淆矩阵,它只会预测female,我们可以计算其准确率 ( 50 + 0 ) / ( 0 + 50 + 50 + 0 ) = 0.5 (50+0)/(0+50+50+0)=0.5 (50+0)/(0+50+50+0)=0.5
又比如我们有一个垃圾邮件识别分类器,其混淆矩阵如下,所示,其准确率为 ( 91 + 4 ) / ( 91 + 4 + 1 + 4 ) = 0.95 (91+4)/(91+4+1+4)=0.95 (91+4)/(91+4+1+4)=0.95:

然后我们有另一个垃圾邮件识别分类器,其混淆矩阵如下所示,其准确率也是 ( 95 + 0 ) / ( 95 + 0 + 0 + 5 ) = 0.95 (95+0)/(95+0+0+5)=0.95 (95+0)/(95+0+0+5)=0.95。(两者用同样的实例数据)
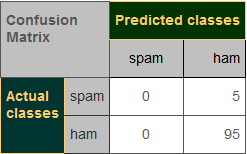
虽然准确率都是0.95但是后者没有分类垃圾邮件的能力,因此分类器的好坏单看准确率是不够的,这就是准确性驳论。
精确率(Precision)和召回率(Recall)
TP:True Positive TN:True Negative FP:False Positive FN:False Negtive(翻译过来就是真阳性,真阴性,假阳性,假阴性)还是英文好记
A c c u r a c y : ( T N + T P ) / ( T N + T P + F N + F P ) Accuracy:(TN+TP)/(TN+TP+FN+FP) Accuracy:(TN+TP)/(TN+TP+FN+FP)
P r e c i s i o n : ( T P ) / ( T P + F P ) Precision:(TP)/(TP+FP) Precision:(TP)/(TP+FP)
R e c a l l : ( T P ) / ( T P + F N ) ( 也 是 T r u e p o s i t i v e r a t e ) Recall:(TP)/(TP+FN)(也是True\quad positive\quad rate) Recall:(TP)/(TP+FN)(也是Truepositiverate)
T r u e n e g t i v e r a t e : ( T N ) / ( T N + F P ) True\quad negtive\quad rate:(TN)/(TN+FP) Truenegtiverate:(TN)/(TN+FP)
多分类的混淆矩阵和准确率,精确率,召回率
A c u r r a c y : Acurracy: Acurracy: ∑ i M i i ∑ i j M i j \frac{\sum_i M_{ii}}{\sum_{ij} Mij} ∑ijMij∑iMii
P e r c i s i o n i : Percision_i: Percisioni: M i i ∑ j M j i \frac{M_{ii}}{\sum_j M_{ji}} ∑jMjiMii
R e c a l l i : Recall_i: Recalli: M i i ∑ j M i j \frac{M_{ii}}{\sum_j M_{ij}} ∑jMijMii
上面这个例子中: A c c u r a c y = ( 6 + 6 + 8 ) / ( 6 + 2 + 1 + 6 + 1 + 1 + 8 ) = 0.8 Accuracy=(6+6+8)/(6+2+1+6+1+1+8)=0.8 Accuracy=(6+6+8)/(6+2+1+6+1+1+8)=0.8 p e r c i s i o n d o g = 6 / ( 6 + 1 + 1 ) = 0.75 percision_{dog}=6/(6+1+1)=0.75 percisiondog=6/(6+1+1)=0.75
p e r c i s i o n c a t = 6 / ( 6 + 1 + 2 ) = 0.67 percision_{cat}=6/(6+1+2)=0.67 percisioncat=6/(6+1+2)=0.67 p e r c i s i o n s n a k e = 8 / ( 0 + 0 + 8 ) = 1 percision_{snake}=8/(0+0+8)=1 percisionsnake=8/(0+0+8)=1
r e c a l l d o g = 6 / ( 6 + 2 + 0 ) = 0.75 recall_{dog}=6/(6+2+0)=0.75 recalldog=6/(6+2+0)=0.75 r e c a l l c a t = 6 / ( 6 + 1 + 0 ) = 0.86 recall_{cat}=6/(6+1+0)=0.86 recallcat=6/(6+1+0)=0.86 r e c a l l s n a k e = 8 / ( 1 + 1 + 8 ) = 0.8 recall_{snake}=8/(1+1+8)=0.8 recallsnake=8/(1+1+8)=0.8
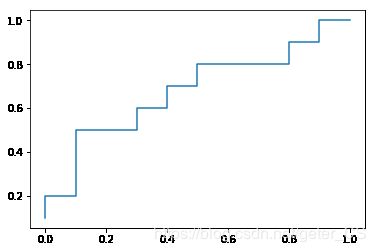
Roc曲线
横 轴 : F a l s e p o s i t i v e r a t e ( F P R ) 表 示 预 测 的 正 例 中 负 例 占 所 有 负 例 的 比 例 : F P R = ( F P ) / ( F P + T N ) 横轴:False positive rate(FPR)表示预测的正例中负例占所有负例的比例:FPR=(FP)/(FP+TN) 横轴:Falsepositiverate(FPR)表示预测的正例中负例占所有负例的比例:FPR=(FP)/(FP+TN)
纵 轴 : T r u e p o s i t i v e r a t e ( T P R ) 表 示 预 测 的 正 例 中 正 例 占 所 有 正 例 的 比 例 : T P R = ( T P ) / ( T P + F N ) 纵轴:True positive rate(TPR)表示预测的正例中正例占所有正例的比例:TPR=(TP)/(TP+FN) 纵轴:Truepositiverate(TPR)表示预测的正例中正例占所有正例的比例:TPR=(TP)/(TP+FN)
T r u e n e g t i v e r a t e ( T N R ) 表 示 预 测 的 负 例 中 负 例 占 所 有 负 例 比 例 : T N R = ( T N ) / ( T N + F P ) True negtive rate(TNR)表示预测的负例中负例占所有负例比例:TNR=(TN)/(TN+FP) Truenegtiverate(TNR)表示预测的负例中负例占所有负例比例:TNR=(TN)/(TN+FP)
所 以 有 T N R = 1 − F P R 所以有TNR=1-FPR 所以有TNR=1−FPR
假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值 θ \theta θ,概率大于等于 θ \theta θ的为正类,小于 θ \theta θ的为负类.对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点.随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大(前者因为FN减少,后者因为FP增加).阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1).
AUC(Area under Curve):Roc曲线下的面积,介于0.1和1之间。Auc作为数值可以直观的评价分类器的好坏,值越大越好。AUC就是从所有正样本中随机选择一个样本,从所有负样本中随机选择一个样本,然后根据你的学习器对两个随机样本进行预测,把正样本预测为正例的概率 p 1 p_1 p1,把负样本预测为正例的概率 p 2 p_2 p2, p 1 > p 2 p_1>p_2 p1>p2的概率就等于AUC.所以AUC反映的是分类器对样本的排序能力.根据这个解释,如果我们完全随机的对样本分类,那么AUC应该接近0.5.
举个例子
现在我们有一个二分类器,20个样本,然后分类结果如下所示.
import pandas as pd
#a=pd.Series([1,2,3,5],index=["a","b","c","d"])
#print(a)
Class=pd.Series([1,1,-1,1,1,1,-1,-1,1,-1,1,-1,1,-1,-1,-1,1,-1,1,-1])
Score=pd.Series([0.9,0.8,0.7,0.6,0.55,0.54,0.53,0.52,0.51,0.505,0.4,0.39,0.38,0.37,0.36,0.35,0.34,0.33,0.30,0.1])
dt={"class":Class,
"score":Score
}
data=pd.DataFrame(dt)
print(data)
class score
0 1 0.900
1 1 0.800
2 -1 0.700
3 1 0.600
4 1 0.550
5 1 0.540
6 -1 0.530
7 -1 0.520
8 1 0.510
9 -1 0.505
10 1 0.400
11 -1 0.390
12 1 0.380
13 -1 0.370
14 -1 0.360
15 -1 0.350
16 1 0.340
17 -1 0.330
18 1 0.300
19 -1 0.100
class表示其真实类别,score表示模型判别其为正类的概率
def FPR(data,threshold):
FP=0
TN=0
for i in range(len(data)):
#print(data.ix[i])
#print(data["class"])
if (data["score"][i]>=threshold)&(data["class"][i]==-1):
FP+=1
if (data["score"][i]<threshold)&(data["class"][i]==-1):
TN+=1
return FP/(FP+TN)
def TPR(data,threshold):
TP=0
FN=0
for i in range(len(data)):
if (data["score"][i]>=threshold)&(data["class"][i]==1):
TP+=1
if (data["score"][i]<threshold)&(data["class"][i]==1):
FN+=1
return TP/(TP+FN)
print("min FPR:",FPR(data,0.9))
print("min TPR:",TPR(data,0.9))
print("max FPR:",FPR(data,0.1))
print("max TPR:",TPR(data,0.1))
min FPR: 0.0
min TPR: 0.1
max FPR: 1.0
max TPR: 1.0
from matplotlib import pyplot as pl
ROC_FPR=[]
ROC_TPR=[]
for threshold in data["score"]:
ROC_FPR.append(FPR(data,threshold))
ROC_TPR.append(TPR(data,threshold))
pl.plot(ROC_FPR,ROC_TPR)
pl.xlabel("FPR")
pl.ylabel()
pl.show()
机器学习分为:监督学习(Supervised learning),无监督学习(Unsupervised learning),半监督学习(Semi-supervised learning),强化学习(Reinforcement learning)