7天微课程day4——时间序列预测的baseline

声明：

1. 本文是系列课程的第4课
2. 本文是对机器学习网站课程的翻译
3. 尊重原作者，尊重知识分享

时间序列预测的baseline

创建一个baseline总是时间序列预测的关键一步。一个baseline可以帮助我们了解模型的好坏。本文将会创建一个基本的时间序列预测模型——persistence模型，该模型的预测可以作为一个baseline。

通过本文，你将学到：

• baseline的重要性。
• 如何从零开始创建一个简单的python时间序列预测模型。
• 如何评估预测结果，如何使用baseline。

Baseline

baseline的作用在于比较，我们通常将预测结果好于baseline的模型保留并舍弃结果差的。一个合理的baseline应该来自一个简单模型，并且不会过多的考虑数据细节方面的特征。

首先，确定数据集、如何划分训练集和测试集、模型评估方法（如MSE）。然后，尽可能选择一个简单的模型快速计算baseline。这个简单的模型应满足一下基本要素：

• 简单，不需要太智能
• 快速，计算速度快
• 可重复，没有太多的trick（所想即所得）

下面介绍最常用的建立baseline的模型——persistence模型。

Persistence Algorithm(又称“naive”预测）

监督学习中最常用的获得baseline的方法是Zero Rule。该方法在分类问题中，总是输出出现次数最多的类；在回归问题中，总是输出平均值。

对于时间序列预测，应该考虑序列中的自相关性，找到更好的计算baseline的方法。

persistence方法用t-1时刻的数据预测t时刻的数据。下面，我们来实现该方法。这里用到的数据集是Shampoo Sales Dataset.

Shampoo Sales Dataset

该数据集是3年里洗发水的月销量，有36个观测值，具体如下：

"Month","Sales"
"1-01",266.0
"1-02",145.9
"1-03",183.1
"1-04",119.3
"1-05",180.3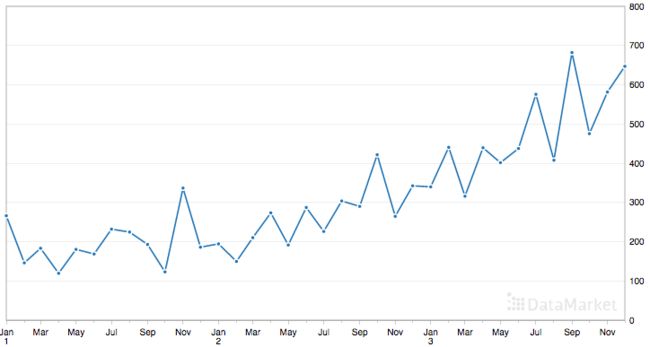

通过洗发水的销量图发现，销量上涨的趋势明显，且有季节性波动。

Persistence Algorithm

我们将分一下几步实现Persistence预测：

1. 先将单变量时间序列转化成监督学习问题。
2. 建立训练集和测试集
3. 定义Persistence模型。
4. 预测并建立baseline
5. 可视化输出

1. 定义监督学习问题

from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot

def parser(x):
    return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# Create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift[1], values], axis=1)
dataframe.columns = ['t-1', 't']
print(dataframe.head())
'''输出
     t-1    t+1
0    NaN  266.0
1  266.0  145.9
2  145.9  183.1
3  183.1  119.3
4  119.3  180.3
'''

2. 训练集和测试集

X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:, 0], train[:, 1]
test_X, test_y = test[:, 0], test[:, 1]

3. Persistence算法

# persistence model
def model_persestence(x):
    return x

4. 预测、评估

预测方法为walk-forward。直接预测是将预测值作为下一步预测的输入；walk-forward用测试集中的真实值作为下一步预测的输入。

# 用真实的t-1时刻的值预测t时刻的值
predictions = list()
for x in test_X:
    yhat = model_persistence(x)
    predictions.append(yhat)
test_score = mean_squared_error(test_y, predictions)
print('Test MSE: %.3f' % test_score)
'''输出
Test MSE: 17730.518
'''

5. 可视化

# plot predictions and expected results
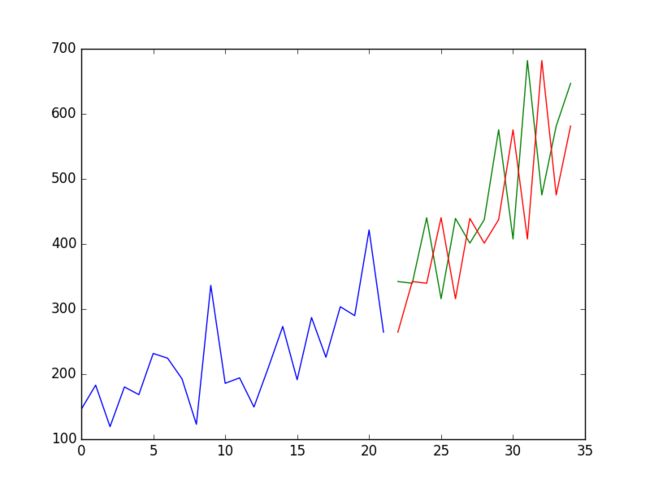
pyplot.plot(train_y)
pyplot.plot([None for i in train_y] + [x for x in test_y])
pyplot.plot([None for i in train_y] + [x for x in predictions])
pyplot.show()