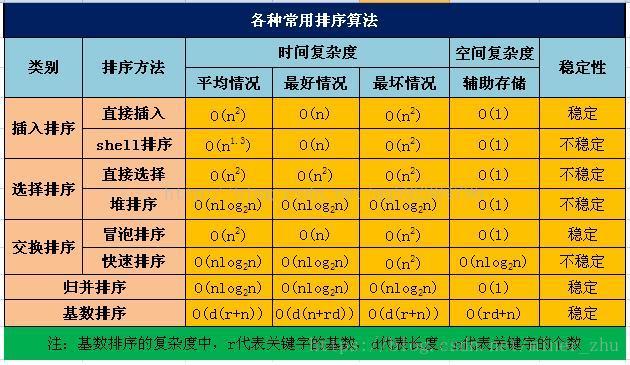
八大经典排序基本思想和python实现
一. 插入排序—直接插入排序
思路:将待插入元素一个个插入到已有序部分
#直接插入排序
def insertSort(arr):
if len(arr) <= 1:
return
for i in range(1,len(arr)):
temp = arr[i]
j = i
while j > 0 and arr[j]>temp:
arr[j] = arr[j-1]
j -= 1
a[j] = temp
二. 插入排序—希尔排序
思路:是直接插入排序算法的一种更高效的改进版本。先将待排序序列按某个增量d(n/2,n为要排序数的个数)分成若干组子序列,对每组使用直接插入法排序,然后再用一个较小的增量(d/2)对它进行分组,重复直接插入排序,继续减少增量直至为1,算法终止
#希尔排序
def shellSort(arr):
if len(arr) <= 1:
return
Increment = len(arr)/2
while Increment > 0:
for i in range(Increment,len(arr)):
temp = arr[i]
j = i
while j>0 and arr[j-Increment] > temp:
arr[j] = arr[j-Increment]
j -= Increment
arr[j] = temp
Increment /= 2
三. 选择排序—简单选择排序
思路:每趟从待排序部分选一个最小值,与待排序部分的第一个元素交换位置
#简单选择排序
def selectSort(arr):
if len(arr) <= 0:
return
for i in range(len(arr-1)):
min = i
for j in range(i+1,len(arr)):
if arr[j] < arr[min]
min = j
arr[min],arr[i] = arr[i],arr[min]
四. 选择排序—堆排序
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
思路:堆排序需要两个过程,一是建立堆(完全二叉树),二是堆顶与堆的最后一个元素交换位置。堆排序会将所有的数据建成一个堆,最大的数据在堆顶,然后将堆顶数据和序列的最后一个数据交换。接下来不动最后一个数据再次重建堆,交换数据,依次下去,就可以排序所有的数据。
#堆排序
def heapSort(arr):
def precDown(a, i, N):
child = 2 * i + 1
tmp = a[i]
while child < N:
if child < N-1 and a[child] < a[child+1]:
child += 1
if tmp < a[child]:
a[i] = a[child]
i = child
else:
break
child = child * 2 + 1
a[i] = tmp
if len(arr) <= 1:
return arr
N = len(arr)
for i in range((N-2)//2, -1, -1):
precDown(arr,i,N)
for i in range(N-1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
precDown(arr,0,i)
五. 交换排序—冒泡排序
思路:相邻元素进行比较决定是否交换,两两比较则最后一个元素应为最大值,对剩余部分重复至结束
#冒泡排序
def bubbleSort(arr):
length = len(arr)
if length <=1:
return
while length>1:
for i in range(length-1):
if arr[i] >arr[i+1]:
arr[i],arr[i+1] = arr[i+1],arr[i]
length -= 1
六. 交换排序—快速排序
思路:选择一个基准,将待排序序列分成都比其大和都比其小的两部分,然后对这两部分数据分别重复进行快速排序
#快速排序
def quick_sort(array, l, r):
if l < r:
q = partition(array, l, r)
quick_sort(array, l, q - 1)
quick_sort(array, q + 1, r)
def partition(array, l, r):
x = array[r]
i = l - 1
for j in range(l, r):
if array[j] <= x:
i += 1
array[i], array[j] = array[j], array[i]
array[i + 1], array[r] = array[r], array[i+1]
return i + 1
七. 归并排序
思路:把待排序序列分为若干个子序列,至每个子序列是有序的,然后再把有序子序列合并为整体有序序列。
#归并排序
def mergeSort(arr):
def Merge(left, right):
i, j = 0, 0
result = []
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
if len(arr) <= 1:
return arr
center = len(arr) / 2
left = mergeSort(arr[:center])
right = mergeSort(arr[center:])
return Merge(left, right)
八. 基数排序
思路:将整数按位数切割成不同的数字,然后按每个位数分别比较。
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
#基数排序
def bucketSort(arr, radix=10):
if len(arr) <= 1:
return arr
K = int(math.ceil(math.log(max(arr), radix)))
bucket = [[] for i in range(radix)]
for i in range(1, K+1):
for element in arr:
bucket[element%(radix**i)/(radix**(i-1))].append(element)
del(arr[:])
for each in bucket:
arr.extend(each)
bucket = [[] for i in range(radix)]
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9), R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1| 不稳定 |
O(1) |
s是所选分组 |
|
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |