HMM和viterbi算法初步实践-----中文分词

马尔科夫性质:当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的（也就是没有任何的关系），那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。

马尔科夫链:状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。也就是马尔可夫性质。在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。

隐马尔可夫模型:是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来作进一步的分析。在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转移概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

三个问题：
1、评估问题：概率计算问题：给定模型和观测序列，计算在模型下观测序列出现的概率。

前向、后向算法解决的是一个评估问题，即给定一个模型，求某特定观测序列的概率，用于评估该序列最匹配的模型。

2、模型学习问题：已知观测序列，估计模型中的参数，使得在该模型下观测序列概率最大，即用极大似然估计的方法估计参数。

Baum-Welch算法解决的是一个模型训练问题，即参数估计，是一种无监督的训练方法，主要通过EM迭代实现；即只有观测序列，无状态序列时训练模型。

极大似然估计：观测序列和相应的状态序列都存在的监督学习算法，用来估计参数。

3、解码问题/预测问题：已知模型和观测序列，给定观测序列，求最可能的对应的状态序列。

维特比算法解决的是给定一个模型和某个特定的输出序列，求最可能产生这个输出的状态序列。如通过海藻变化（输出序列）来观测天气（状态序列），是预测问题，通信中的解码问题。

中文分词实践
  代码主要来源于《Python自然语言处理实战：核心技术与算法》(github)一书，对其中一些地方略作修改。这里我们主要运用维特比算法将中文分词转化为HMM的解码问题。
  HMM主要理论概念参考后文链接,这里主要讲解下代码的大致思路：规定每个字最多只有四个构词位置:B(词首)、M(词中)、E(词尾)和S(单独成词)。在分词任务中,o为B、M、E、S这4中标记,$\lambda$为句子中的每个字符,例如"北" “京”（包括标点等非中文字符）。在HMM中，将$P({\lambda }_k|o_k)$称为发射概率,$P(o_k|o_{k-1})$称为转移概率。通过设置$P(o_k|o_{k-1})=0$，可以排除类似BBB、EM等不合理的组合。

  在HMM中，求解 $maxP(\lambda |o)P(o)$的常用方法是 Veterbi 算法。 它是一种动态规划方法，核心思想是 : 如果最终的最优路径经过某个$o_i$， 那么从初始节点到$o_{i-1}$点的路径必然也是一个最优路径一一因为每一个节点。$o_i$ 只会影响前后两个$P(o_{i-1}|o_i)$和$P(o_i|o_{i+1})$。

  根据这个思想，可以通过递推的方法，在考虑每个$o_i$时只需要求出所有经过各 $o_{i-1}$的候选点的最优路径， 然后再与当前的$o_i$结合比较。 这样每步只需要算不超过$L^2$次，就可以逐步找出最优路径。 Viterbi 算法的效率是$O(n\ast L^2)$，L是候选数目最多的节点$o_i$的候选数目，它正比于 n， 这是非常高效率的。 HMM 的状态转移图如下图所示:

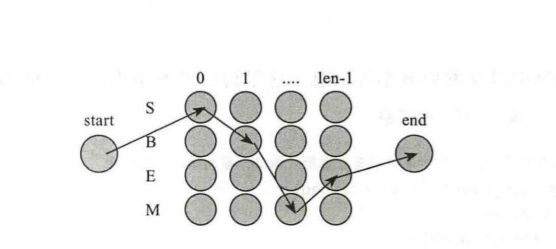
HMM代码如下:

class HMM(object):
    # 初始化全局信息
    def __init__(self):
        # 主要是用于存取算法中间结果，不用每次都训练模型
        self.model_file = './chapter-3/data/hmm_model.pkl'

        # 状态值集合
        self.state_list = ['B', 'M', 'E', 'S']  # B:词首 M:词中 E:词尾 S:单独成词
        # 参数加载,用于判断是否需要重新加载model_file
        self.load_para = False

    # 用于加载已计算的中间结果，当需要重新训练时，需初始化清空结果
    def try_load_model(self, trained):
        if trained:
            import pickle
            with open(self.model_file, 'rb') as f:  # pkl 二进制文件,需用rb
                self.A_dic = pickle.load(f)
                self.B_dic = pickle.load(f)
                self.Pi_dic = pickle.load(f)
                self.load_para = True

        else:
            # 状态转移概率（状态->状态的条件概率）
            self.A_dic = {}
            # 发射概率（状态->词语的条件概率）
            self.B_dic = {}
            # 状态的初始概率
            self.Pi_dic = {}

            self.load_para = False

    # 计算转移概率、发射概率以及初始概率
    def train(self, path):

        # 重置几个概率矩阵
        self.try_load_model(False)

        # 统计状态出现次数，求p(o)
        Count_dic = {}

        # 初始化参数
        def init_parameters():
            for state in self.state_list:
                self.A_dic[state] = {s: 0.0 for s in self.state_list}
                self.Pi_dic[state] = 0.0
                self.B_dic[state] = {}

                Count_dic[state] = 0

        # 对词进行标注
        def makeLabel(text):
            out_text = []
            if len(text) == 1:
                out_text.append('S')
            else:
                out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']

            return out_text

        init_parameters()
        line_num = -1
        # 观察者集合，主要是字以及标点等
        words = set()
        with open(path, encoding='utf8') as fp:
            for line in fp:
                line_num += 1

                line = line.strip()
                if not line:
                    continue

                word_list = [i for i in line if i != ' ']
                words |= set(word_list)  # 更新字的集合

                linelist = line.split()  # 默认空字符串分割

                line_state = []
                for w in linelist:
                    line_state.extend(makeLabel(w))

                assert len(word_list) == len(line_state)  # 每个字对应一个状态

                for k, v in enumerate(line_state):
                    Count_dic[v] += 1  # 各状态在句子中出现次数
                    if k == 0:
                        self.Pi_dic[v] += 1  # 每个句子的第一个字的状态，用于计算初始状态概率
                    else:
                        self.A_dic[line_state[k - 1]][v] += 1  # 记录前状态->现状态的次数
                        self.B_dic[line_state[k]][word_list[k]] = \
                            self.B_dic[line_state[k]].get(word_list[k], 0) + 1.0  # 记录状态->字的次数

        self.Pi_dic = {k: v * 1.0 / line_num
                       for k, v in self.Pi_dic.items()}  # 计算状态(B,S)的初始概率
        self.A_dic = {
            k: {k1: v1 / Count_dic[k]
                for k1, v1 in v.items()}
            for k, v in self.A_dic.items()  # 例:B->S =n(BS)/n(S)
        }  # 状态转移矩阵

        #加1平滑
        self.B_dic = {
            k: {k1: (v1 + 1) / Count_dic[k]
                for k1, v1 in v.items()}
            for k, v in self.B_dic.items()
        }
        #序列化
        import pickle
        with open(self.model_file, 'wb') as f:
            pickle.dump(self.A_dic, f)
            pickle.dump(self.B_dic, f)
            pickle.dump(self.Pi_dic, f)

        return self

    # 求最大概率的路径 text:切词文本 states:状态集合 start_p:初始概率 trans_p:转移矩阵 emit_p:发射概率
    def viterbi(self, text, states, start_p, trans_p, emit_p):
        V = [{}]
        path = {}

        # 分别计算出(B S E M)->text[0]各个概率
        for y in states:
            V[0][y] = start_p[y] * emit_p[y].get(text[0], 0)
            path[y] = [y]

        for t in range(1, len(text)):
            V.append({})
            newpath = {}

            # 检验训练的发射概率矩阵中是否存在该字
            neverSeen = text[t] not in emit_p['S'].keys() and \
                text[t] not in emit_p['M'].keys() and \
                text[t] not in emit_p['E'].keys() and \
                text[t] not in emit_p['B'].keys()
            for y in states:
                emitP = emit_p[y].get(text[t],
                                      0) if not neverSeen else 1.0  # 设置未知字单独成词

                # 文本过长,超过一定的迭代,会导致计算结果趋近于零,报错:ValueError: max() arg is an empty sequence
                (prob, state) = max([(V[t - 1][y0] * trans_p[y0].get(y, 0), y0)
                                     for y0 in states if V[t - 1][y0] > 0
                                     ])  # 计算出V[t-1]各状态到当前状态概率的最大值   state:前一状态

                V[t][y] = prob * emitP
                newpath[y] = path[state] + [y]
            path = newpath

        if emit_p['M'].get(text[-1], 0) > emit_p['S'].get(text[-1], 0):
            (prob, state) = max([(V[len(text) - 1][y], y) for y in ('E', 'M')])
        else:
            (prob, state) = max([(V[len(text) - 1][y], y) for y in states])

        return (prob, path[state])  # 返回概率最大的那条路径

    def cut(self, text):
        import os
        if not self.load_para:
            self.try_load_model(os.path.exists(self.model_file))  # 读取已保存模型参数
        prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic,
                                      self.A_dic, self.B_dic)
        begin, next = 0, 0
        for i, char in enumerate(text):
            pos = pos_list[i]
            if pos == 'B':
                begin = i
            elif pos == 'E':
                yield text[begin:i + 1]
                next = i + 1
            elif pos == 'S':
                yield char
                next = i + 1
        if next < len(text):
            yield text[next:]


hmm = HMM()
hmm.train('./data/trainCorpus.txt_utf8')

text = '这里是北京时间八点整'
res = hmm.cut(text)
print(text)
print(str(list(res))) # ['这里', '是', '北京', '时间', '八点', '整']

参考文章：
隐马尔可夫(HMM)、前/后向算法、Viterbi算法
《Python自然语言处理实战：核心技术与算法》
viterbi算法通俗理解
如何通俗地讲解 viterbi 算法
如何用简单易懂的例子解释隐马尔可夫模型?
隐马尔可夫模型（一）——马尔可夫模型
隐马尔可夫(HMM)、前/后向算法、Viterbi算法 再次总结