EMD和VMD

作者：桂。

时间：2017-03-06  20:57:22

链接：http://www.cnblogs.com/xingshansi/p/6511916.html 

---

前言

本文为Hilbert变换一篇的内容补充，主要内容为：

　　1）EMD原理介绍

　　2）代码分析

　　3）一种权衡的小trick

　　4）问题补充

内容主要为自己的学习总结，并多有借鉴他人，最后一并给出链接。

一、EMD原理介绍

　　A-EMD的意义

很多人都知道EMD(Empirical Mode Decomposition)可以将信号分解不同频率特性，并且结合Hilbert求解包络以及瞬时频率。EMD、Hilbert、瞬时频率三者有无内在联系？答案是：有。

按照Hilbert变换一篇的介绍，

f(t)=dΦ(t)d(t)f(t)=dΦ(t)d(t)

然而，这样求解瞬时频率在某些情况下有问题，可能出现f(t)f(t)为负的情况：我1秒手指动5下，频率是5Hz；反过来，频率为8Hz时，手指1秒动8下，可如果频率为-5Hz呢？负频率没有意义。

考虑信号

x(t)=x1(t)+x2(t)=A1ejω1t+A2ejω2t=A(t)ejφ(t)x(t)=x1(t)+x2(t)=A1ejω1t+A2ejω2t=A(t)ejφ(t)

为了简单起见，假设A1A1和A2A2恒定，且ω1ω1和ω2ω2是正的。信号x(t)x(t)的频谱应由两个在ω1ω1和ω2ω2的δδ函数组成，即

X(ω)=A1δ(ω−ω1)+A2δ(ω−ω2)X(ω)=A1δ(ω−ω1)+A2δ(ω−ω2)

因为假设ω1ω1和ω2ω2是正的，所以该信号解析。求得相位

Φ(t)=A1sinω1t+A2sinω2tA1cosω1t+A2cosω2tΦ(t)=A1sin⁡ω1t+A2sin⁡ω2tA1cos⁡ω1t+A2cos⁡ω2t

分别取两组参数，对tt求导，得到对应参数下的瞬时频率：

参数：

ω1=10Hzω1=10Hz和ω2=20Hzω2=20Hz.

• 组1：{A1=0.2,A2=1A1=0.2,A2=1};
• 组2：{A1=1.2,A2=1A1=1.2,A2=1}

对于组2，瞬时频率出现了负值。

可见：

对任意信号进行Hilbert变换，可能出现无法解释、缺乏实际意义的频率分量。Norden E. Hung等人对瞬时频率进行研究后发现，只有满足特定条件的信号，其瞬时频率才具有物理意义，并将此类信号成为：IMF/基本模式分量。　

　　B-EMD基本原理

此处给一个原理图：

　　C-基本模式分量（IMF）

EMD分解的IMF其瞬时频率具有实际物理意义，原因有两点：

• 限定1：
  • 在整个数据序列中，极值点的数量NeNe（包括极大值、极小值点）与过零点的数量必须相等，或最多相差1个，即(Ne−1)≤Ne≥(Ne+1)(Ne−1)≤Ne≥(Ne+1).
• 限定2：
  • 在任意时间点titi上，信号局部极大值确定的上包络线fmax(t)fmax(t)和局部极小值确定的下包络线fmin(t)fmin(t)的均值为0.

限定1即要求信号具有类似传统平稳高斯过程的分布；限定2要求局部均值为0，同时用局部最大、最小值的包络作为近似，从而信号局部对称，避免了不对称带来的瞬时频率波动。

　　D-VMD

关于VMD(Variational Mode Decomposition)，具体原理可以参考其论文，这里我们只要记住一点：其分解的各个基本分量——即各解析信号的瞬时频率具有实际的物理意义。

 

二、代码分析

首先给出信号分别用VMD、EMD的分解结果:

给出对应的代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61

%--------------- Preparation clear all; close all; clc; % Time Domain 0 to T T = 1000; fs = 1/T; t = (1:T)/T; freqs = 2*pi*(t-0.5-1/T)/(fs); % center frequencies of components f_1 = 2; f_2 = 24; f_3 = 288; % modes v_1 = (cos(2*pi*f_1*t)); v_2 = 1/4*(cos(2*pi*f_2*t)); v_3 = 1/16*(cos(2*pi*f_3*t)); % for visualization purposes wsub{1} = 2*pi*f_1; wsub{2} = 2*pi*f_2; wsub{3} = 2*pi*f_3; % composite signal, including noise f = v_1 + v_2 + v_3 + 0.1*randn(size(v_1)); % some sample parameters for VMD alpha = 2000;        % moderate bandwidth constraint tau = 0;            % noise-tolerance (no strict fidelity enforcement) K = 4;              % 4 modes DC = 0;             % no DC part imposed init = 1;           % initialize omegas uniformly tol = 1e-7;   %--------------- Run actual VMD code [u, u_hat, omega] = VMD(f, alpha, tau, K, DC, init, tol); subplot(size(u,1)+1,2,1); plot(t,f,'k');grid on; title('VMD分解'); subplot(size(u,1)+1,2,2); plot(freqs,abs(fft(f)),'k');grid on; title('对应频谱'); for i = 2:size(u,1)+1     subplot(size(u,1)+1,2,i*2-1);     plot(t,u(i-1,:),'k');grid on;     subplot(size(u,1)+1,2,i*2);     plot(freqs,abs(fft(u(i-1,:))),'k');grid on; end   %---------------run EMD code imf = emd(f); figure; subplot(size(imf,1)+1,2,1); plot(t,f,'k');grid on; title('EMD分解'); subplot(size(imf,1)+1,2,2); plot(freqs,abs(fft(f)),'k');grid on; title('对应频谱'); for i = 2:size(imf,1)+1     subplot(size(imf,1)+1,2,i*2-1);     plot(t,imf(i-1,:),'k');grid on;     subplot(size(imf,1)+1,2,i*2);     plot(freqs,abs(fft(imf(i-1,:))),'k');grid on; end

　　附上两个子程序的code.

VMD:

+ View Code

EMD:

+ View Code

关于EMD，有对应的工具箱。VMD也有扩展的二维分解，此处不再展开。

 

三、一种权衡的小trick

关于瞬时频率的原理以及代码，参考另一篇博文。

比较来看：

• EMD分解的IMF分量个数不能人为设定，而VMD(Variational Mode Decomposition)则可以;
• 但VMD也有弊端：分解过多，则信号断断续续，没有多少规律可言。

能不能取长补短呢？

自己之前做了一个小code，放在这里，供大家交流使用（此理论为自己首创，版权所有，拿去也不介意！(●'◡'●)）。
给定一个信号,下图是EMD分解结果，分解出了5个分量。

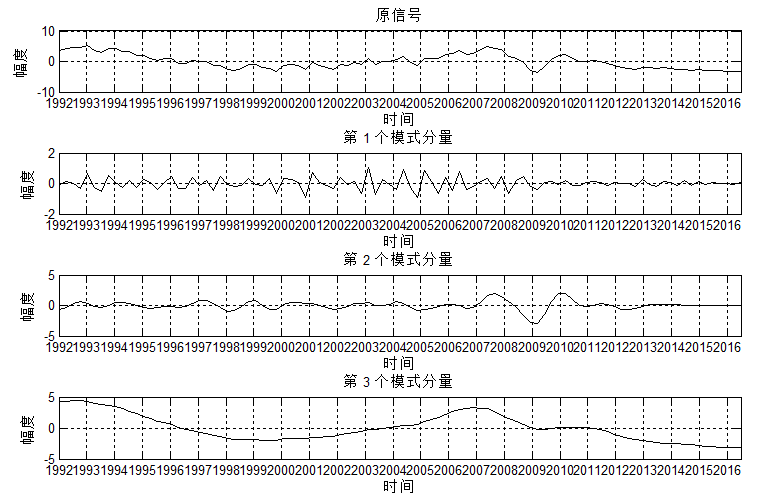
再来一个VMD（设定分量个数为3）的分解结果：

比较两个结果，可以发现：VMD的低频分量，更容易表达出经济波动的大趋势，而EMD则不易观察该特性。
或许有人会说：几个EMD分量叠加一下，也会有该效果，但如果不观察分解的数据，如何确定几个分量相加呢？更何况EMD总的IMF个数也是未知！

VMD的优势观察到了，但如何确定分量个数呢？
再来一个效果图：

这里分析了VMD分量从1~9，9种情况下某特征的曲线，可以观察到：个数增加到一定数量，曲线有了明显的下弯曲现象（该特性容易借助曲率，进行量化分析，不再展开），这个临界的个数就是分解的合适数量，此处：K=3，因为到4就有了明显的下弯曲。

可见通过该特征，即可理论上得出最优K。下面讲一讲这个某特征为何物？
上一段代码：

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

for st=1:9     K=st+1;     [u, u_hat, omega] = VMD(data, length(data), 0, K, 0, 1, 1e-5);     u=flipud(u);     resf=zeros(1,K);     for i=1:K         testdata=u(i,:);         hilbert(testdata');          z=hilbert(testdata');                   % 希尔伯特变换         a=abs(z);                               % 包络线         fnor=instfreq(z);                       % 瞬时频率         resf(i)=mean(fnor);          end     subplot(3,3,st)     plot(resf,'k');title(['个数为',num2str(st)]);grid on; end

 

　　没错，该特征就是：分量瞬时频率的均值。如果分解个数过大，则分量会出现断断絮絮地现象，特别是在高频，这样一来，即使是高频，平均瞬时频率反而低一些，这也是下弯曲的根本原因。

这个小trick就介绍到这里。

 

四、问题补充

HHT算法中，有两处存在端点效应，VMD是否也有呢？这一点没有再去验证。另外，关于Hilbert的端点效应，在另一篇博文已经给出。