量子计算入门基础学习笔记(三 )
一入量子深似海
- 一 . 量子态叠加与量子态纠缠
- 二 ,算符补充,表象与矩阵
- 1.泡利算符(Pauli)
- 2. 表象,算符的本征值与本征矢量
欢迎来到量子计算学习的第三课,接着上次博客中对张量的介绍,本次学习我们都如雷贯耳的量子态的叠加和纠缠,除此之外,我们补充泡利算符的相关内容
一 . 量子态叠加与量子态纠缠
在 从线性代数到量子力学中,我们浅谈过量子叠加的一些东西,薛定谔的猫就是这个的最好例子,除此之外,量子态的纠缠与其是同等重要的,下面我们来好好说一说二者之间的区别与联系!
先感性的再理解一下这个量子态的纠缠:
在量子力学里,当几个粒子在彼此相互作用后,由于各个粒子所拥有的特性已综合成为整体性质,无法单独描述各个粒子的性质,只能描述整体系统的性质,则称这现象为量子缠结或量子纠(quantum entanglement)。量子纠缠是一种纯粹发生于量子系统的现象;在经典力学里,找不到类似的现象!经典物理中的光 和 波也存在也存在此关联,但是它反映在概率不相乘上,而量子的纠缠却反映在概率幅的不相乘上!
二者联系:概率叠加是纠缠的基础。纠缠就是在概率叠加基础之上,再加上其它约束条件。没有概率叠加,就没有纠缠。比如两个光子纠缠,实际是指两个光子的自旋态,首先必须是叠加态,事先不确定。如果两个光子的自旋态是事先确定的,那就不可能纠缠。然后两个光子的自旋,加起来还要守恒,两个光子的自旋,必须是一正一负,不能是其它情况,这就是纠缠!
通俗的说,你有一双鞋,分别把一只鞋子放进不同的两只盒子里,置于南北两极。在你打开鞋盒之前,鞋盒里的鞋子有左脚和 右脚两种状态的可能,而在你打开鞋盒的那一刹那,状态就锁死在了其中一个状态,这个叫叠加!在你打开鞋盒之后,如果你看到的是左脚,那置于地球另一端的就一定是右脚,这个叫纠缠!
什么叫好的文章,我这就是好的文章,先用一大堆高大上的东西给你整懵逼,然后用人类能听得见,看的懂的 人话 让你理解的明明白白的,这个时候 你内心已经喊了无数句卧槽了。关注点起来!!

区别是啥啊?前一篇学习博客中最后一部分介绍了张量乘积的相关东西,为的就是解释这个:
1 2 ∣ 00 ⟩ + 1 2 ∣ 10 ⟩ = 1 2 ∣ 0 ⟩ ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ ∣ 0 ⟩ \frac{1}{\sqrt 2} \left| 00 \right \rangle + \frac{1}{\sqrt 2} \left| 10 \right \rangle = \frac{1}{\sqrt 2} \left| 0 \right \rangle \left| 0 \right \rangle + \frac{1}{\sqrt 2} \left| 1 \right \rangle \left| 0 \right \rangle 21∣00⟩+21∣10⟩=21∣0⟩∣0⟩+21∣1⟩∣0⟩
这显然是一个量子叠加态,我们可以 “提取公因式”!
( 1 2 ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ ) ∣ 0 ⟩ \left ( \frac{1}{\sqrt 2} \left| 0 \right \rangle + \frac{1}{\sqrt 2} \left| 1 \right \rangle \right ) \left| 0 \right \rangle (21∣0⟩+21∣1⟩)∣0⟩
由于最后一位量子比特都是 ∣ 0 ⟩ \left| 0 \right \rangle ∣0⟩ ,故而可以写成量子比特 ( 1 2 ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ ) \left ( \frac{1}{\sqrt 2} \left| 0 \right \rangle + \frac{1}{\sqrt 2} \left| 1 \right \rangle \right ) (21∣0⟩+21∣1⟩) 与 ∣ 0 ⟩ \left| 0 \right \rangle ∣0⟩的乘积!那如果不能写成乘积的形式呢?
1 2 ∣ 01 ⟩ + 1 2 ∣ 10 ⟩ \frac{1}{\sqrt 2} \left| 01 \right \rangle + \frac{1}{\sqrt 2} \left| 10 \right \rangle 21∣01⟩+21∣10⟩
此式无论采用什么办法都无法写成量子比特的乘积,这个叠加状态就称为量子纠缠状态!它的意义可是非同凡向响!
量子态可以叠加的物理特性是实现量子并行计算的基础。
说到这个并行处理的能力,我们举个例子:10进制数10和无,先转成二进制,再用量子比特表示:
∣ 10 ⟩ 10 = ∣ 1 ⟩ ⨂ ∣ 0 ⟩ ⨂ ∣ 1 ⟩ ⨂ ∣ 0 ⟩ ⨂ ∣ 5 ⟩ 10 = ∣ 0 ⟩ ⨂ ∣ 1 ⟩ ⨂ ∣ 0 ⟩ ⨂ ∣ 1 ⟩ ⨂ \left| 10 \right \rangle_{10} =\left| 1 \right \rangle \bigotimes \left| 0 \right \rangle \bigotimes \left| 1\right \rangle \bigotimes \left| 0 \right \rangle \bigotimes \\ \left| 5 \right \rangle_{10} =\left| 0 \right \rangle \bigotimes \left| 1 \right \rangle \bigotimes \left| 0\right \rangle \bigotimes \left| 1 \right \rangle \bigotimes ∣10⟩10=∣1⟩⨂∣0⟩⨂∣1⟩⨂∣0⟩⨂∣5⟩10=∣0⟩⨂∣1⟩⨂∣0⟩⨂∣1⟩⨂
取他们的叠加态就得到如下所示:
∣ 10 ⟩ 10 + ∣ 5 ⟩ 10 = ∣ 1010 ⟩ + ∣ 0101 ⟩ = ∣ 1 ⟩ ⨂ ∣ 0 ⟩ ⨂ ∣ 1 ⟩ ⨂ ∣ 0 ⟩ ⨂ \left| 10 \right \rangle_{10}+ \left| 5 \right \rangle_{10}= \left| 1010 \right \rangle+ \left|0101\right \rangle=\\ \left| 1 \right \rangle \bigotimes \left| 0 \right \rangle \bigotimes \left| 1\right \rangle \bigotimes \left| 0 \right \rangle \bigotimes ∣10⟩10+∣5⟩10=∣1010⟩+∣0101⟩=∣1⟩⨂∣0⟩⨂∣1⟩⨂∣0⟩⨂
传统的计算机只会在转化编码之后先算10再算5,而量子算法可以同时计算10与5,达到并行计算!
二 ,算符补充,表象与矩阵
上期博客我们的重点之一便是算符的学习,但是由于一些限制因素没能介绍完,我们接着上次算符的部分继续肝!
1.泡利算符(Pauli)
下面请屏幕前的你迅速的抽出纸和笔,和我一起计算:
四个Paui 门:
σ 0 = I = ∣ 0 ⟩ ⟨ 0 ∣ + ∣ 1 ⟩ ⟨ 1 ∣ = ( 1 0 0 0 ) + ( 0 0 0 1 ) = ( 1 0 0 1 ) σ 1 = σ 1 = ∣ 0 ⟩ ⟨ 1 ∣ + ∣ 1 ⟩ ⟨ 0 ∣ = ( 0 1 1 0 ) \sigma_{0} =I =\left| 0 \right \rangle \left \langle 0 \right |+\left| 1 \right \rangle \left \langle 1 \right | =\begin{pmatrix}1& 0 \\0 & 0 \end{pmatrix}+\begin{pmatrix}0& 0 \\0 & 1\end{pmatrix}=\begin{pmatrix}1& 0 \\0 & 1\end{pmatrix} \\ \sigma_{1} =\sigma_{1}=\left| 0 \right \rangle \left \langle 1 \right |+\left| 1 \right \rangle \left \langle 0\right | =\begin{pmatrix} 0& 1 \\ 1 & 0 \end{pmatrix} σ0=I=∣0⟩⟨0∣+∣1⟩⟨1∣=(1000)+(0001)=(1001)σ1=σ1=∣0⟩⟨1∣+∣1⟩⟨0∣=(0110)
σ 2 = σ y = − i ∣ 0 ⟩ ⟨ 1 ∣ + i ∣ 1 ⟩ ⟨ 0 ∣ = ( 0 − i i 0 ) σ 3 = σ z = Z = ∣ 0 ⟩ ⟨ 0 ∣ − ∣ 1 ⟩ ⟨ 1 ∣ = ( 1 0 0 − 1 ) \sigma_{2} =\sigma_{y}=-i \left| 0 \right \rangle \left \langle 1 \right |+i \left| 1 \right \rangle \left \langle 0\right | =\begin{pmatrix} 0& -i \\ i & 0 \end{pmatrix} \\ \sigma_{3} =\sigma_{z}=Z=\left| 0 \right \rangle \left \langle 0 \right |- \left| 1 \right \rangle \left \langle 1\right | =\begin{pmatrix} 1& 0 \\ 0 & -1 \end{pmatrix} σ2=σy=−i∣0⟩⟨1∣+i∣1⟩⟨0∣=(0i−i0)σ3=σz=Z=∣0⟩⟨0∣−∣1⟩⟨1∣=(100−1)
在此基础上,我们会发现Pauli算符都是幺正算符:
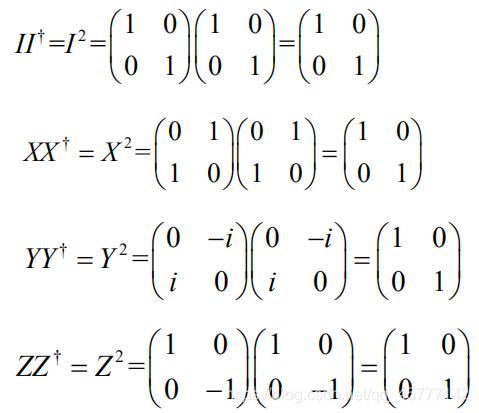
此外,泡利矩阵的行列式和它们的迹分别为:
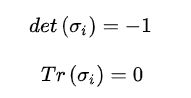
故从上述关系可以推得每个泡利矩阵 σ i \sigma _{i} σi的本征值分别为 ±1!
2. 表象,算符的本征值与本征矢量
把记忆的时间轴拉到大一的线代课中,作为线代中的核心知识,特征值与特征向量一定在大家的脑海中留下了难以磨灭的深刻印象!
我们在量子力学入门学习的专栏中也向大家较为详细的介绍了这二者与量子中本征值与,征矢量之间的前世今生了!
到这里,既然算符的本质是矩阵,那么算符的本征值与本征矢量又是啥样的呢?
A ∣ α ⟩ = λ ∣ α ⟩ A\left| \alpha \right \rangle =\lambda \left| \alpha \right \rangle A∣α⟩=λ∣α⟩
这里的定义几乎和线代中的是一模一样, ∣ α ⟩ \left| \alpha \right \rangle ∣α⟩,是线性算符A的本征矢量, λ \lambda λ是与其本征矢量对应的本征值,在这里注意 λ \lambda λ是复数(但是厄米算符的本征值确是实数)!该方程被称为本征方程!
在 从线性代数到量子力学中,曾记否我们学习过的“坐标表象”?
在量子计算中,我们选取一组基矢如 { ∣ v 1 ⟩ , ∣ v 2 ⟩ , ⋯ ∣ v n ⟩ } \left \{ \left| v_{1}\right \rangle ,\left| v_{2}\right \rangle ,\cdots \left| v_{n}\right \rangle \right \} {∣v1⟩,∣v2⟩,⋯∣vn⟩},也就是我们线代中都学习过的一组极大线性无关组,也叫表象!
表象之间可以互相转化, 通过一个幺正变换 S S S, 可以从正交归一基 ∣ v i ⟩ \left| v_{i} \right \rangle ∣vi⟩变化为 ∣ v i ′ ⟩ \left| v_{i}^{'} \right \rangle ∣∣∣vi′⟩ , 即:
∣ v i ′ ⟩ = ∑ j S i j ∣ v i ⟩ ( i = 1 , 2 , 3 ⋯ , n ) \left| v_{i}^{'} \right \rangle =\sum_{j}S_{ij}\left| v_{i} \right \rangle \qquad (i=1,2,3\cdots,n) ∣∣∣vi′⟩=j∑Sij∣vi⟩(i=1,2,3⋯,n)
到这里我感觉大部分人的理解只能停留在我上述的文字表面(好吧,我代表不了 大部分人),let me introduce a simple example ,which may help you feel better! 请原谅我这蹩脚的 English!
先抛开量子,我们在牛顿力学体系中的坐标(表象)变换!那些高数里面基础的东西我在这里就不再赘述了!
为了描述三维空间中一个质点的运动,我们常采用直角坐标系的方法。标记为 A ( x , y , z , t ) A(x,y,z,t) A(x,y,z,t),也可写为矢量的形式;
r ( t ) A = x ( t ) i → + y ( t ) j → + j ( t ) k → r(t)_{A} = x(t) \overrightarrow{i}+y(t) \overrightarrow{j}+j(t) \overrightarrow{k} r(t)A=x(t)i+y(t)j+j(t)k
如果这个质点在一球壳上运动,那么采用求坐标计算会比较简单,质点的位置可记为: ( r , θ , ϕ ) (r,\theta ,\phi ) (r,θ,ϕ),其运动轨迹方程为:
r ( t ) A = a 1 ( t ) r → + a 2 ( t ) θ → + a 3 ( t ) ϕ → r(t)_{A} = a_{1}(t)\overrightarrow{r} +a_{2}(t)\overrightarrow{\theta } +a_{3}(t)\overrightarrow{\phi } r(t)A=a1(t)r+a2(t)θ+a3(t)ϕ
那么问题来了,都是表达一个球面,这二者表达的方式之间如何转化呢?
如果一个质点做圆周运动,坐标矢量可: 简写为 r ( t ) = θ ( t ) r(t)=\theta (t) r(t)=θ(t),经过位移和角位移的变换,速度和; 角速度的变换,加速度和角加速度的变换后,直线运动的公式完全转化为圆周运动的公式,可见经过简单的坐标变换,原本非常复杂的圆周运动和一维直线运动本质上得到了统一!转化过程:
{ x = r s i n θ c o s ϕ y = r s i n θ s i n ϕ z = r c o s θ ⇒ { i → = x 1 r → + x 2 θ → + x 3 ϕ → j → = y 1 r → + y 2 θ → + y 3 ϕ → z → = z 1 r → + z 2 θ → + z 3 ϕ → \begin{cases} x=r\;sin\theta cos\phi \\ y=r\;sin\theta sin\phi \\ z=rcos\theta \end{cases} \Rightarrow \begin{cases} \overrightarrow{i}=x_{1}\overrightarrow{r} +x_{2}\overrightarrow{\theta }+x_{3}\overrightarrow{\phi } \\ \overrightarrow{j}=y_{1}\overrightarrow{r} +y_{2}\overrightarrow{\theta }+y_{3}\overrightarrow{\phi } \\ \overrightarrow{z}=z_{1}\overrightarrow{r} +z_{2}\overrightarrow{\theta }+z_{3}\overrightarrow{\phi } \end{cases} ⎩⎪⎨⎪⎧x=rsinθcosϕy=rsinθsinϕz=rcosθ⇒⎩⎪⎪⎨⎪⎪⎧i=x1r+x2θ+x3ϕj=y1r+y2θ+y3ϕz=z1r+z2θ+z3ϕ
至此我们认识到若能得到同一位置矢量 r ( x , y , z ) r(x,y,z) r(x,y,z)或者 ( r , θ , ϕ ) (r,\theta ,\phi ) (r,θ,ϕ)在不同的坐标系中的转换公式,也就是说我们只要求得了坐标变换矩阵 S S S,就会很容易在不同坐标系红任意变换,like these:
( x ( t ) y ( t ) z ( t ) ) = ( x 1 x 2 x 3 y 1 y 2 y 3 z 1 z 2 z 3 ) ( r ( t ) θ ( t ) ϕ ( t ) ) ⇒ r ( x , y , z ) = S r ( r , θ , ϕ ) \begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix}=\begin{pmatrix} x_{1} & x_{2} &x_{3} \\ y_{1} & y_{2} &y_{3} \\ z_{1} & z_{2} &z_{3} \\ \end{pmatrix} \begin{pmatrix} r(t) \\ \theta (t) \\ \phi (t) \end{pmatrix} \Rightarrow r(x,y,z)=S\;r(r,\theta, \phi ) ⎝⎛x(t)y(t)z(t)⎠⎞=⎝⎛x1y1z1x2y2z2x3y3z3⎠⎞⎝⎛r(t)θ(t)ϕ(t)⎠⎞⇒r(x,y,z)=Sr(r,θ,ϕ)
现在我们将其类比推理到量子力学中去:
假设有F和G两个力学量算符,他们的本征方程分别为:
F ^ ψ n = F n ψ n G ^ ϕ n = G n ϕ n \widehat{F}\psi_{n}=F_{n}\psi_{n} \qquad \widehat{G}\phi _{n}=G_{n}\phi _{n} F ψn=FnψnG ϕn=Gnϕn
ψ n \psi_{n} ψn 与 ϕ n \phi _{n} ϕn 分别构成完备的坐标基矢!任意的波函数 ψ \psi ψ 可在不同的表象中展开:
F表象中: ψ = c 1 ψ 1 + c 2 ψ 2 + ⋯ + c n ψ n + ∑ n c n ψ n \psi =c_{1}\psi _{1} +c_{2}\psi _{2}+\cdots+c_{n}\psi _{n}+\sum_{n}c_{n}\psi _{n} ψ=c1ψ1+c2ψ2+⋯+cnψn+∑ncnψn,其中 ψ n \psi _{n} ψn为F表象基矢。
G表象中: ψ = b 1 ϕ 1 + b 2 ϕ 2 + ⋯ + b n ϕ n = ∑ n b n ϕ n \psi =b_{1}\phi _{1}+b_{2}\phi _{2}+\cdots+b_{n}\phi _{n}=\sum_{n}b_{n}\phi _{n} ψ=b1ϕ1+b2ϕ2+⋯+bnϕn=∑nbnϕn,其中 ϕ n \phi _{n} ϕn为G表象基矢!
上述两种表象表示的是同一种量子态,只是选取的坐标系不同,而且不同的表象之间可以相互转化!
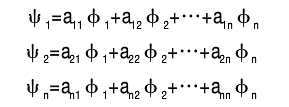
类比我们可以的到其幺正矩阵为:
S = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ) S=\begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{pmatrix} S=⎝⎜⎜⎜⎛a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎠⎟⎟⎟⎞
现在大家应该理解的更深刻一点了吧!
好的,本次博客学习就到这里了,觉得博主写的还能看下去的劳您点个关注 ,点点赞!

