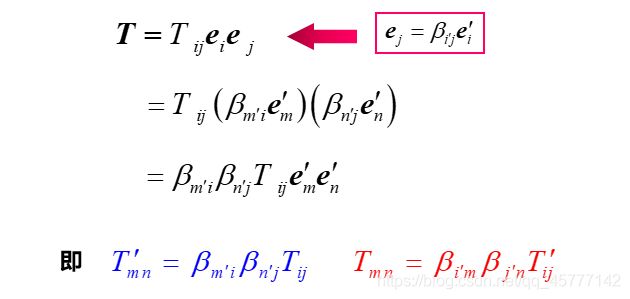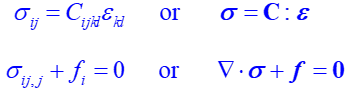张量基础学习（二 . 坐标变换，分量转化规律与张量方程 ）
欢迎来到张量基础学习的第二弹，本次将持续深入学习相关知识，觉着本人写的对您多少有帮助的麻烦点点关注，养成先赞再看的好习惯！
Tensors learning
- 一 . 坐标与坐标转换
- 二. 张量分量转换规律与张量方程
- （1）张量分量转换规律
- （2）张量方程
一 . 坐标与坐标转换
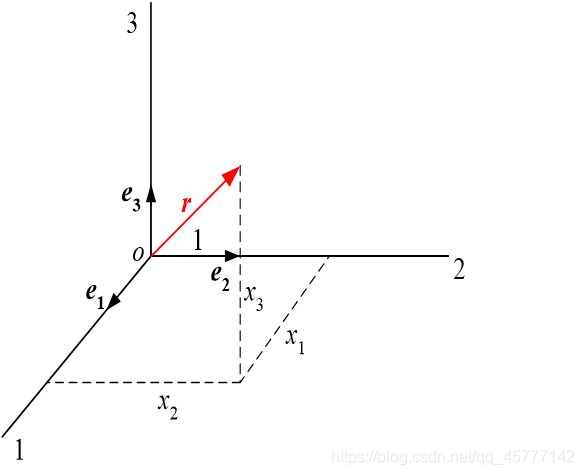
在笛卡尔坐标系中：
其中有：
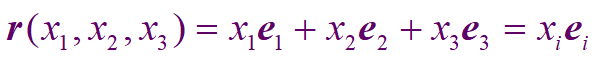
这都是我们中学常用的一些向量的基本套路！在其他的非笛卡尔坐标系中， r = r ( x 1 , x 2 , x 1 ) r=r(x_{1},x_{2},x_{1}) r=r(x1,x2,x1), 当坐标系发生变化时候，矢径 变化为：
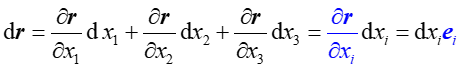
这里的矢径就是这个r矢量！
下面我们来认识几个简单的概念：
（1）基矢量：
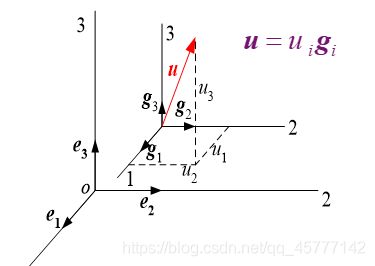
矢径对坐标的偏导数定义的三个基矢量 g i g_{i} gi:
g i = ∂ r ∂ x 1 ( i = 1 , 2 , 3 ) \boldsymbol{g}_{i}=\frac{\partial \boldsymbol{r}}{\partial x_{1}} \qquad(i = 1,2,3) gi=∂x1∂r(i=1,2,3)
（2）参考架(单位向量)：
空间每点处有三个基矢量，它们组成一个参考架或称坐标架。任何具有方向性的物理量都可以对其相应作用点处的参考架分解。例如对于笛卡尔坐标系：
g 1 = ∂ r ∂ x 1 = e 1 ; g 2 = ∂ r ∂ x 2 = e 2 ; g 3 = ∂ r ∂ x 3 = e 3 \boldsymbol{g}_{1}=\frac{\partial \boldsymbol{r}}{\partial x_{1}}=\boldsymbol{e}_{1} ; \boldsymbol{g}_{2}=\frac{\partial \boldsymbol{r}}{\partial x_{2}}=\boldsymbol{e}_{2} ; \boldsymbol{g}_{3}=\frac{\partial \boldsymbol{r}}{\partial x_{3}}=\boldsymbol{e}_{3} g1=∂x1∂r=e1;g2=∂x2∂r=e2;g3=∂x3∂r=e3
了解了这些基本概念之后，我们来看一看坐标变换的具体操作，在这之前，先认识欧式空间中的一般坐标系有几个特性：
- 现在的坐标线可能不再正交。
- 不同点处的坐标线可能不再平行。
- 基矢量的大小和方向都可能随点而异。
- 各点处的参考架不再是正交标准化基。
为了让大家更好的理解这个变换（其实非常简单），废话不多说，先上图：
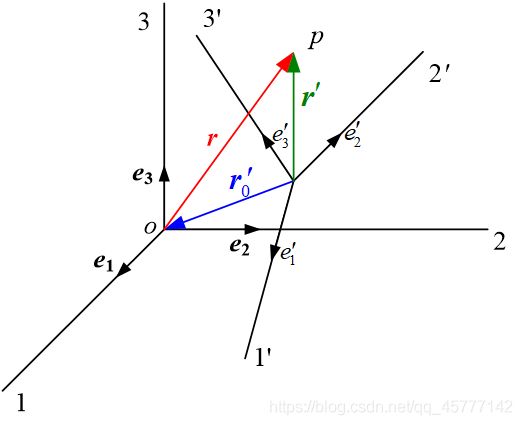我们直接在原来坐标系旁边建立一组新的正交基矢，然后重新标号并且连线！
同样的，这三个新基底和原来一样满足：
e i ′ ⋅ e j ′ = δ i j ； e i ⋅ e j = δ i j {e_{i}}'\cdot{e_{j}}'= \delta_{ij}；e_{i}\cdot e_{j} = \delta_{ij} ei′⋅ej′=δij；ei⋅ej=δij
下面我们引入一组新的转化系数 β i ′ j \beta _{{i}'j} βi′j，以老基为基底分解新底:
e i ′ = β i 1 e 1 + β i 2 e 2 + β i 3 e 3 = ∑ β i j e j e_{i}^{\prime}=\beta_{i 1} e_{1}+\beta_{i 2} e_{2}+\beta_{i 3} e_{3}=\sum \beta_{i j} e_{j} ei′=βi1e1+βi2e2+βi3e3=∑βijej
其中，这里的转化系数易得：
β i j = cos ( e i ′ , e j ) = e i ′ ⋅ e j = e j ⋅ e i ′ \beta_{i j}=\cos \left(e_{i}^{\prime}, e_{j}\right)=e_{i}^{\prime} \cdot e_{j}=e_{j} \cdot e_{i}^{\prime} βij=cos(ei′,ej)=ei′⋅ej=ej⋅ei′
那么，举一反三，以新基为基底分解老基：
e j = β 1 ′ j e 1 ′ + β 2 ′ j e 2 ′ + β 3 ′ e 3 ′ = β i ′ j e i ′ e_{j}=\beta_{{1}' j} e_{1}^{\prime}+\beta_{2^{\prime} j} e_{2}^{\prime}+\beta_{3^{\prime}} e_{3}^{\prime}=\beta_{{i}'j} e_{i}^{\prime} ej=β1′je1′+β2′je2′+β3′e3′=βi′jei′
进一步，其中的 r ′ , r 0 ′ , r {r}',{r_{0}}' ,r r′,r0′,r三种关系用三角形法则展示为： r ′ = r 0 ′ + r {r}' ={r_{0}}' +r r′=r0′+r
通过这三个不同的r，我们将新坐标系与原坐标系形成了一种联系，能够让我们实现其中矢量相互转换的联系：
r ′ = x i ′ e i ′ , r = x j e j , r 0 ′ = ( x i ′ ) 0 e i ′ \boldsymbol{r}^{\prime}=x_{i}^{\prime} \boldsymbol{e}_{i}^{\prime}, \quad \boldsymbol{r}=x_{j} \boldsymbol{e}_{j}, \quad \boldsymbol{r}_{0}^{\prime}=\left(x_{i}^{\prime}\right)_{0} e_{i}^{\prime} r′=xi′ei′,r=xjej,r0′=(xi′)0ei′
要想实现坐标转变，需要将原坐标系中的目标矢量投影到新坐标中，即用 e i ′ {e_{i}}' ei′点乘 r ′ = r 0 ′ + r {r}' ={r_{0}}' +r r′=r0′+r的左右两边！
- 左边：
r ′ ⋅ e i ′ = x k ′ e k ′ ⋅ e i ′ = x k ′ δ k i = x i ′ \boldsymbol{r}^{\prime} \cdot \boldsymbol{e}_{i}^{\prime}=x_{k}^{\prime} \boldsymbol{e}_{k}^{\prime} \cdot \boldsymbol{e}_{i}^{\prime}=x_{k}^{\prime} \delta_{k i}=x_{i}^{\prime} r′⋅ei′=xk′ek′⋅ei′=xk′δki=xi′ - 右边：
( r + r 0 ′ ) ⋅ e i ′ = x j e j ⋅ e i ′ + ( x k ′ ) 0 e k ′ ⋅ e i ′ = x j β i j + ( x i ′ ) 0 \left(r+r_{0}^{\prime}\right) \cdot e_{i}^{\prime}=x_{j} e_{j} \cdot e_{i}^{\prime}+\left(x_{k}^{\prime}\right)_{0} e_{k}^{\prime} \cdot e_{i}^{\prime}=x_{j} \beta_{i j}+\left(x_{i}^{\prime}\right)_{0} (r+r0′)⋅ei′=xjej⋅ei′+(xk′)0ek′⋅ei′=xjβij+(xi′)0
之后，我们便可以用这两个公式根据实际情况灵活的变换不同坐标系中的矢量！
根据上一篇博客中学到的爱因斯坦求和约定以及指标相关知识，我们可以将它展开成矩阵的形式（坐标原点未变）：
{ x 1 ′ x 2 ′ x 3 ′ } = [ β 1 ′ 1 β 1 ′ 2 β 1 ′ 3 β 2 ′ 1 β 2 ′ 2 β 2 ′ 3 β 3 ′ 1 β 3 ′ 2 β 3 ′ 3 ] { x 1 x 2 x 3 } \left\{\begin{array}{l}x_{1}^{\prime} \\ x_{2}^{\prime} \\ x_{3}^{\prime}\end{array}\right\}=\left[\begin{array}{lll}\beta_{1^{\prime} 1} & \beta_{1^{\prime} 2} & \beta_{1^{\prime} 3} \\ \beta_{2^{\prime} 1} & \beta_{2^{\prime} 2} & \beta_{2^{\prime} 3} \\ \beta_{3^{\prime} 1} & \beta_{3^{\prime} 2} & \beta_{3^{\prime} 3}\end{array}\right]\left\{\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right\} ⎩⎨⎧x1′x2′x3′⎭⎬⎫=⎣⎡β1′1β2′1β3′1β1′2β2′2β3′2β1′3β2′3β3′3⎦⎤⎩⎨⎧x1x2x3⎭⎬⎫
或： { x ′ } = [ β ] { x } \quad\left\{x^{\prime}\right\}=[\beta]\{x\} {x′}=[β]{x}
{ x 1 x 2 x 3 } = [ β 1 ′ 1 β 2 ′ 1 β 3 ′ 1 β 1 ′ 2 β 2 ′ 2 β 3 ′ 2 β 1 ′ 3 β 2 ′ 3 β 3 ′ 3 ] { x 1 ′ x 2 ′ x 3 ′ } \left\{\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right\}=\left[\begin{array}{lll}\beta_{1^{\prime} 1} & \beta_{2^{\prime} 1} & \beta_{3^{\prime} 1} \\ \beta_{1^{\prime} 2} & \beta_{2^{\prime} 2} & \beta_{3^{\prime} 2} \\ \beta_{1^{\prime} 3} & \beta_{2^{\prime} 3} & \beta_{3^{\prime} 3}\end{array}\right]\left\{\begin{array}{l}x_{1}^{\prime} \\ x_{2}^{\prime} \\ x_{3}^{\prime}\end{array}\right\} ⎩⎨⎧x1x2x3⎭⎬⎫=⎣⎡β1′1β1′2β1′3β2′1β2′2β2′3β3′1β3′2β3′3⎦⎤⎩⎨⎧x1′x2′x3′⎭⎬⎫
或 { x } = [ β ] T { x ′ } \quad\{x\}=[\beta]^{\mathrm{T}}\left\{x^{\prime}\right\} {x}=[β]T{x′}
一般情况下我们运用这个的时候没有那么复杂，转化公式一般都包含在一个函数方程里面，下面我们来正式定义一下 坐标转换 ：
设在三维欧氏空间中任选两个新、老坐标系， x i ′ {x_{i}}' xi′ 和 x j x_{j} xj 是同一空间点P的新、老坐标值，则方程组
x i ′ = x i ′ ( x j ) ( i , j = 1 , 2 , 3 ) x_{i}^{\prime}=x_{i}^{\prime}\left(x_{j}\right) \quad(i, j=1,2,3) xi′=xi′(xj)(i,j=1,2,3)
定义了由老坐标到新坐标的坐标变换，称为：正变换，反之，我们称其为逆变换：
x j = x j ( x i ′ ) ( i , j = 1 , 2 , 3 ) x_{j} = x_{j}({x_{i}}')\quad(i, j=1,2,3) xj=xj(xi′)(i,j=1,2,3)
我们再对第一个红色定义式微分得：
d x i ′ = ∂ x i ′ ∂ x j d x j \mathrm{d} x_{i}^{\prime}=\frac{\partial x_{i}^{\prime}}{\partial x_{j}} \mathrm{d} x_{j} dxi′=∂xj∂xi′dxj
前面的系数为 J J J(雅克比行列式)：
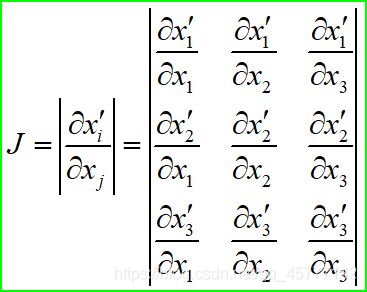
同样的，要学会举一反三，这是对应正变换的，需要逆变换就反过来 d x i ′ d\;{x_{i}}' dxi′,唯一确定 d x j d\;x_{j} dxj 。
二. 张量分量转换规律与张量方程
（1）张量分量转换规律
通过前面的简单学习，我们知道，张量都不会因人为选择参考系的改变而改变，但是张量分量的值则与坐标系的选择密切相关！
其实非常好理解，想象一下我们一起用正交分解法分解矢量的时候，是需要依赖参考系的，所以不同的坐标系会让分量产生些许的变化！所以，张量的分量在坐标转化得时候应满足一定的规律以确保其坐标不变性！
先以三维空间的二阶张量为例，其分解成：
其中这个 T i j T_{ij} Tij 为张量分量 ， e i e j e_{i}e_{j} eiej也就是 基矢量
以此类推，再根据之前坐标转换的相关知识，张量分量转化规律为：
还有一些小规律，大家看一下有个印象就行：
在一个表示全部张量分量集合的指标符号 T i j k ⋯ T_{ijk\cdots} Tijk⋯ 中，自由指标的数目等于张量的阶数 K，每个自由指标的取值范围等于张量的维数 n，各指标在其取值范围内的任何一种可能组合都表示了张量的一个分量，所以 n 维 K 阶张量共有 nK 个分量
（2）张量方程
要探索张量分量的值与坐标系变换的规律，那就离不开方程组的应用。所谓张量方程，就是每一项都是张量的方程，我们初中之前学过的标量方程，在物理中学的矢量方程，在线性代数中学的矩阵方程都是张量方程。张量方程具有一条神奇的特性：与坐标选择无关，换言之，解出来的结果不随坐标系变化而变化。因此，张量方程可以用于描述客观物理现象的固有性质和普遍规律。
好 本期张量学习的博客就到这里的，觉得还能看的，对您有帮助的不要忘记点赞关注！