自然语言处理1-马尔科夫链和隐马尔科夫模型(HMM)
基于统计的语言模型比基于规则的语言模型有着天然的优势,而(中文)分词是自然语言处理的基础,接下来我们将注重介绍基于统计的中文分词及词性标注技术。为此做以下安排:首先介绍一下中文处理涉及到基本概念,接着分析开源的一些基于统计的中文分词原理。
中文分词涉及的基本概念有马尔科夫链,隐马尔科夫模型(HMM),Ngram模型,最大熵马尔科夫模型(MEMM),条件随机场(CRF)等
1、马尔科夫链
通俗讲马尔科夫链是指在某一状态空间序列中,当前的状态只与它前面n(n=1,2,……)个状态相关。
具体定义如下:
马尔科夫链指具有马尔科夫性质的随机变量X1, X2, X3,…序列,即将来的状态只与当前的状态相关,而与过去的状态无关。
用数学公式表示如下
Pr (Xn+1=|X1=x1,X2=x2, …, Xn=xn) = Pr (Xn+1=x|Xn=xn)
Xn(n=1,2,3,…)表示所有可能取值的集合,被称为“状态空间”,而Xn的值则是在时间n的状态
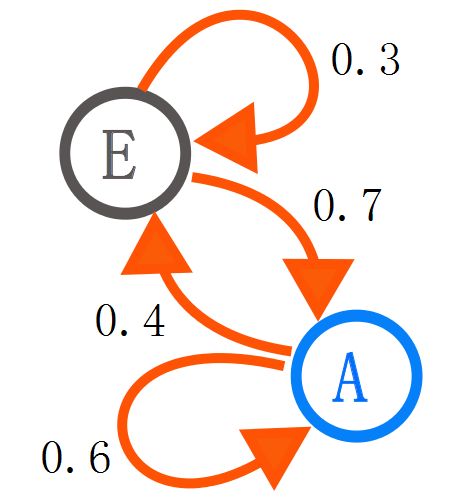
马尔科夫链通常被描述成一个有向图,其中状态表示图的顶点,状态转移概率表示图的边。如图1所示。
图1-两个状态的马尔科夫链
2、隐马尔科夫模型
HMM定义
一个HMM是一个三元组![]()
![]() 初始状态概率向量
初始状态概率向量
A =(aij): 状态转移概率;Pr(xi|xj)
B=(bij) : 混淆矩阵;Pr(yi|xj)
这其中,所有的状态转移概率和混淆概率在整个系统中都是一成不变的。这也是HMM中最不切实际的假设。
一个HMM模型主要是由两类状态和三组概率来表示的
两类状态:观察状态,隐藏状态
三组概率:初始概率,状态转移概率及两态对应概率。
举例
我们通过一个词性标注的例子来阐述一下HMM的原理
观察状态:他 是 计算机 博士
隐藏状态:代词,动词,名词 名词
假设根据语料我们可以得到隐藏状态两两状态之间的转换如下所示,我们也叫它状态转移概率矩阵。
|
|
代词 |
动词 |
名词 |
| 代词 |
0.5 |
0.25 |
0.25 |
| 动词 |
0.375 |
0.125 |
0.375 |
| 名词 |
0.125 |
0.625 |
0.375 |
根据语料库,也可以得到两态对应概率矩阵即混淆矩阵,如下所示:
|
|
他 |
是 |
计算机 |
博士 |
| 代词 |
0.60 |
0.20 |
0.15 |
0.05 |
| 动词 |
0.25 |
0.25 |
0.25 |
0.25 |
| 名词 |
0.05 |
0.10 |
0.35 |
0.50 |
同时我们假定初始的概率满足下面所示:
代词 动词 名词
〔0.63 0.17 0.20〕
![]()
至此我们根据语料统计并训练了一个词性标注的HMM模型。
有了HMM模型,我们可以做什么呢?
(1)、评估即根据已知的HMM找出一个观察序列的概率。例如我们可以评估(他 是 计算机 博士)出现的概率。我们可以通过forward algorithm算法来得到观察状态序列对应于一个HMM的概率。
(2)、根据观察状态序列找到产生这一序列的潜在的隐含状态序列,如根据“他 是 计算机 博士”序列找到其对应的“代词 动词 名词 名词”状态序列。我们可以通过viterbialgorithm来解决。
可以根据训练好的隐马尔科夫模型来做评估和解码的问题,那么隐马尔科夫模型又是怎么得到呢?
这是与HMM相关的问题中最难的,根据一个观察序列(来自于已知的集合),以及与其有关的一个隐藏状态集,估计一个最合适的隐马尔科夫模型(HMM),也就是确定对已知序列描述的最合适的(,A,B)三元组。当矩阵A和B不能够直接被(估计)测量时,前向-后向算法(forward-backward algorithm)被用来进行学习(参数估计),这也是实际应用中常见的情况。
由于直接用前向-后向算法(forward-backward algorithm)进行学习的准确性不是非常高,目前通用的做法是通过人工标注语料库生成HMM。但需要注意的是人工标注语料库工作量比较大。
隐马尔科夫模型的缺点:
HMM模型中存在两个假设:一是输出观察值之间严格独立,二是状态的转移过程中当前状态只与前一状态有关(一阶马尔可夫模型)。
在下面的例子里
观察状态:他 是 计算机 博士
隐藏状态:代词,动词,名词 名词
比如在计算Pr(博士|名词)概率时不会考虑“博士”的上下文信息“计算机”;还有第一个“名词”出现的概率只与前面的“动词”出现的概率相关,这样表示上下文信息的能力就比较有限。