【论文阅读】mixup: BEYOND EMPIRICAL RISK MINIMIZATION

mixup: BEYOND EMPIRICAL RISK MINIMIZATION

作者Hongyi Zhang，本科北大，发这篇文章的时候是MIT的博士五年级学生。这篇文章是和FAIR的人一起合作的。

Introduction

摘要中，本文提到了mixup方法可以让神经网络倾向于训练成简单的线性关系。从而降低模型的过拟合现象。

实际上，现在的神经网络规模通常是和数据集规模成正比的。训练神经网络时应用的主要指导思想是经验风险最小化(ERM)。但是ERM收敛的重要保证就是模型规模不会随着数据规模的增加而增加。实际上，越大的数据集使用越大的网络，只能说明网络“记住了”这些图片，即使在随机给定的标签上深度网络都会有很好的的效果。因此，这样的网络对于不在数据分布内的样本(adversarial examples )效果非常差。

从ERM到mixup

机器学习的目的是为了使期望风险最小化

R(f)=∫ℓ(f(x),y)dP(x,y) R ( f ) = ∫ ℓ ( f ( x ) , y ) d P ( x , y )

其中， ℓ ℓ 表示损失函数。但是一般而言 dP(x,y) d P ( x , y ) 是未知的。因此我们会退而求其次，最小化经验风险（ERM）:

Pδ(x,y)=1n∑i=1nδ(x=xi,y=yi) P δ ( x , y ) = 1 n ∑ i = 1 n δ ( x = x i , y = y i )

这里的 δ δ 为Dirac mass，（里面为11则为1，否则为0）。事实上就是每个样本赋予相同的权重 1n 1 n 。

得到了估计的分布后，可以用来估算期望风险了。

Rδ(f)=∫ℓ(f(x),y)dPδ(x,y)=1n∑i=1nℓ(f(xi),yi) R δ ( f ) = ∫ ℓ ( f ( x ) , y ) d P δ ( x , y ) = 1 n ∑ i = 1 n ℓ ( f ( x i ) , y i )

但是这样就会造成一个问题：只要模型能够记住每个样本，就可以最小化经验风险。因此一旦出现和模型分布轻微不同的数据，表现就会很差。其实就是过拟合了。

有人就提出，能不能不用ERM，而是用VRM（Vicinal Risk Mnimization，最小化邻近风险）。

Pν(x,y)=1n∑i=1nν(x~,y~|xi,yi) P ν ( x , y ) = 1 n ∑ i = 1 n ν ( x ~ , y ~ | x i , y i )

其中， ν ν 是临近分布，即在 (xi,yi) ( x i , y i ) 附近找到 (x~,y~) ( x ~ , y ~ ) 的概率。比如之前的一个工作，假设 ν(x~,y~|xi,yi)=N(x~−xi,σ2)δ(y~=yi) ν ( x ~ , y ~ | x i , y i ) = N ( x ~ − x i , σ 2 ) δ ( y ~ = y i ) ，就等价于在原始数据上加高斯噪声。（这个用脚后跟想想就能想明白）

为了使用VRM，这篇文章首先基于临近分布采样出一个增强的数据集 Dν:=(x~i,y~i)mi=1 D ν := ( x ~ i , y ~ i ) i = 1 m ,并且在这个数据集上使用经验-邻近风险：

Rν(f)=1m∑i=1nℓ(f(x~i),y~i) R ν ( f ) = 1 m ∑ i = 1 n ℓ ( f ( x ~ i ) , y ~ i )

这篇文章的主要贡献在于提出了一种通用的临近分布，mixup（公式太长我就直接截图了哈）：

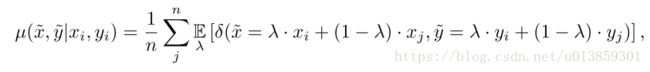
其中， λ∼Beta(α,α) λ ∼ Beta ( α , α ) ,对于任意的 α∈(0,∞) α ∈ ( 0 , ∞ ) 。简而言之，从mixup分布采样出数据集：

x~=λxi+(1−λ)xj,y~=λyi+(1−λ)yj, x ~ = λ x i + ( 1 − λ ) x j , y ~ = λ y i + ( 1 − λ ) y j ,

这里 (xi,yi) ( x i , y i ) 和 (xj,yj) ( x j , y j ) 是从数据集中随机采样得到的任意两个样本。 α α 是一个超参数，用于控制混合的程度。当 α α 越接近于0时，分布越倾向于集中在 (0,1) ( 0 , 1 ) 的两端，越大时分布越均匀。极限情况 α=0 α = 0 时等价于没有采用本方法。

mixup的实现也是非常直观的。图一(a)是其实现的Pytorch代码。实现上有下面几种考虑：

1. 我们也考虑过三个或者三个以上的标签做混合，但是效果几乎和两个一样，而且增加了mixup过程的时间。
2. 当前的mixup使用了一个单一的loader获取minibatch，对其随机打乱后，mixup对同一个minibatch内的数据做混合。这样的策略和在整个数据集随机打乱效果是一样的，而且还减少了IO的开销。
3. 在同种标签的数据中使用mixup不会造成结果的显著增强。

所以mixup到底做了什么事情呢？其实就是告诉训练器，尽可能训练出线性的边界来。这样就会减少过拟合了。而且线性模型最简单，符合奥卡姆剃刀。图1 b显示了数据是过渡的，提供了对于不确定度更为柔和的估计。图2评估了他们在CIFAR-10训练过程的i凹陷。可以看出mixup更加稳定一些。

实验部分

又双叒叕吊打了之前的方法，直接上图：