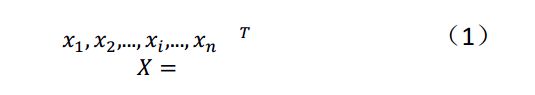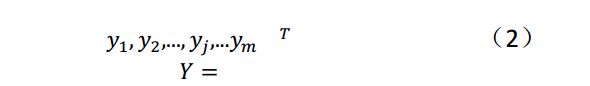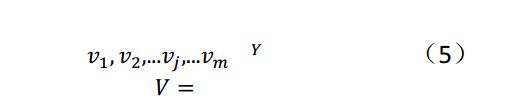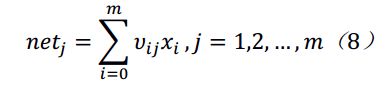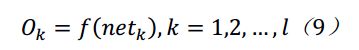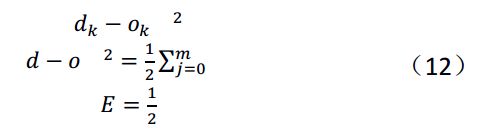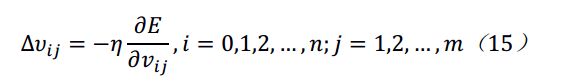数据结构课设报告之“BP神经网络的实现”
GitHub地址。
课程编号:0521172B 课程性质:必修
数据结构课程设计报告
院 系:计算机与信息系
班 级:物联网工程17-2班
姓 名:XXX
学 号: 201721XXXX
指导教师:XX
选题名称:BP神经网络的实现
2019年1月20日 至 2019年2月15日
目录
- 数据结构课程设计报告 ……...…...…......…...……......……...…......…….........…....……...…0
- 一、实验概述:...................................................................................................................4
-
1.1课程设计题目:...................................................................................................4
-
1.2课程设计目的:...................................................................................................4
-
1.3系统主要内容与功能:........................................................................................4
-
1.3.1 设计内容:..............................................................................................4
-
1.3.2 设计功能:..............................................................................................4
-
1.3.3 实验环境和工具:...................................................................................7
- 二、实验原理:...................................................................................................................7
-
2.1 结构构成:.........................................................................................................7
-
2.2 算法流程:.........................................................................................................8
-
2.3 数学原理:………….……….……………………………….................…………...9
-
三、实验结果:...................................................................................................................9
- 四、算法分析:.................................................................................................................16
- 五、总结:…………………………………………………………...........…………………….17
- 附录(源程序):.............................................................................................................18
- 参考文献:........................................................................................................................31
- 查重结果:........................................................................................................................31
一、实验概述:
1.1课程设计题目:
本设计题为BP神经网络的实现,主要任务是利用 C++语言实现BP神经网络, 并利用BP神经网络解决螨虫分类问题。
1.2课程设计目的:
主要有这些:
1、熟悉自己所学的多种数据结构;
2、理解BP神经网络的工作原理;
3、利用C++实现BP神经网络;
4、利用BP神经网络实现螨虫分类。
1.3系统主要内容与功能:
1.3.1设计内容:
设定好学习样本个数,取样本个数的训练数据存储于文本文档中,在C++ main函数中设定学习效率和步长,读取训练输入和对应的输出进行训练,通过训练得到对应的权值,然后进行数据测试。
1.3.2设计功能:
本课程设计由3个主要功能实现,它们分别为初始化数据,训练和测试螨虫分类是否准确。
①初始化数据:
srand( (unsigned)time( NULL ) );
for( int i = 0; i < HN; i ++ )
{
for( int j = 0; j < INnum; j ++ )
{
W[i][j] = double( rand() % 100 ) / 100; //初始化输入层到隐层的权值
}
}
for( int ii = 0; ii < ONnum; ii ++ )
{
for( int jj = 0; jj < HN; jj ++ )
{
V[ii][jj] = double( rand() % 100 ) / 100; //初始化隐层到输出层的权值
}
}这段代码是为了初始化输入层到隐层的权值,以及隐层到输出层的权值。
input_sample(int m):这段代码是为了初始化训练数据的输入值。
output_sample(int m):这个函数是为了初始化数据对应的输出值
②训练:
本功能主要是逐步训练,直至收敛。
calculate_HIDDEN_OUTPUT():本函数主要用于求隐层输出。
calculate_OUTPUT_OUTPUT():本函数主要用于求输出层输出。
inaccuracy_Output_Hidden(int m);本函数主要用于求解输出层到隐层的一般化误差
inaccuracy_Hidden_Input():本函数主要用于求解隐层到输入层的一般化误差。
update_Output_Hidden:本函数主要是用于调整输出层至隐层的权值。
update_Hidden_Input:本函数主要是用于调整隐层至输入层的权值。 saveWeight():本函数主要是用于保存计算出来的权值。
③测试分类是否准确:
数据结构:
struct
{
double input[INnum];
double teach[ONnum];
}Study_Data[SampleCount];代表了训练样本;
double Weight_Input[NUM_HIDDEN][mInputNode];
代表了输入层至隐藏层权值;
double Weight_Output[mOutPutNode][NUM_HIDDEN];
代表了隐层至输出层权值;
double Sample_Input[mInputNode];
代表了单个样本输入数据;
double Sample_Output[mOutPutNode];
代表了单个样本期望输出值;
double ORIGIN_W[NUM_HIDDEN][mInputNode];
代表了隐藏层到输入层的旧权数组;
double ORIGIN_V[mOutPutNode][NUM_HIDDEN];
代表了输出层到隐藏层的旧权数组;
double HIDDEN_INPUT[NUM_HIDDEN];
代表了隐层的输入;
double OUTPUT_INPUT[mOutPutNode];
代表了输出层的输入;
double hidenLayerOutput[NUM_HIDDEN];
代表了隐层的输出;
double OUTPUT_OUTPUT[mOutPutNode];
代表了输出层的输出;
double inaccuracy_sample[SampleCount];
代表了第m个样本的总误差。
1.3.3实验环境与工具:
①操作系统:Windows企业版2016长期服务版;
②开发工具:Visual Studio 2017社区版;
③开发语言:C++。
二、实验原理:
2.1结构构成:
BP神经网络是一种根据误差逆向传播的多层前馈网络。其由输入层,隐藏层和输出层构成的。它模拟了人脑的神经网络的结构,众所周知,人大脑传递信息的基本单位是神经元,人脑中有大量的神经元,每个神经元与多个神经元相连接,就是这样,构成了人的大脑。人的大脑的神经网络传播是按照一定的规律,不是神经元会对所有传过来的刺激进行反应。首先是积累刺激,而BP神经网络,类似于上述,是一种简化的生物模型。每层神经网络都是由神经元构成的,单独的每个神经元相当于一个感知器。输入层是单层结构的,输出层也是单层结构的,而隐藏层可以有多层,也可以是单层的。输入层、隐藏层、输出层之间的神经元都是相互连接的,为全连接。总得来说,BP神经网络结构就是,输入层得到刺激后,会把他传给隐藏层,至于隐藏层,则会根据神经元相互联系的权重并根据规则把这个刺激传给输出层,输出层对比结果,如果不对,则返回进行调整神经元相互联系的权值。这样就可以进行训练,最终学会,这就是BP神经网络模型。
2.2算法流程:
①先把统一处理过的训练样本输入到BP神经网络。
②设定步长,学习效率,最大学习次数,生成初始权值,阈值。
③计算从输入层开始到输出层结束的各层的输入输出值。
④计算输出层的误差,如果误差小于设定误差,便结束。如果大于设定误差,便调整权值和阈值,执行步骤③。
2.3数学原理:
在三层BP神经网络中,输入向量,也就是输入层神经元为:
隐藏层输入向量,也就是隐藏层神经元:
输出层输出向量,也就是输出层神经元:
期望输出向量可以表示为:
输入层到隐藏层之间的权值用数学向量可以表示为:
这里面的列向量vj为隐藏层第 j 个神经元对应的权重;隐藏层到输出层之间
的权值用数学向量可以表示为:
式(6)中的列向量wk为输出层第 k 个神经元对应的权重。
输入层,隐藏层,输出层之间的数学关系如下所示:
就输出层而言
就隐藏层而言
在上述表达式中,激活函数 f(x)必须为单调函数,我们选取 sigmoid 函数:
由于 f(x)是连续函数,是可导函数,且f'(x)=f(x)[1-f(x)]。
这些就构成了 BP 神经网络的输入层,输出层和隐藏层。
| 如果 BP 网络的输出结果和期望输出结果不一致时,那么便有了输出误差 E,表达式如下: |
展开到隐藏层,则有如下表达式:
根据这些,我们可以明白, BP 神经网络的输入误差产生是由于输出层到隐藏层的权值和隐藏层到输入层的权值决定,因此调整输出层到隐藏层的权值和隐藏层到输入层的权值可以改变误差 E。
显而易见的,调整输出层到隐藏层的权值和隐藏层到输入层的权值的思想是让这个误差不断缩小这样才能满足我们的要求,因此我们需要让这些权值修改量与误差 E 的负梯度下降量成正比,也就是如下表达式:
式(14)、(15)中常数
反映了学习效率。
综上所述,通过数学原理可以看出,在 BP 学习算法中,输入层,输出层和隐藏层权值调整方式都是一样的。由三个条件决定,它们分别是:学习效率,输入层,输出层和隐藏层的各层误差信号和各层输入信号 X/Y。其中最为重要的是输出层误差信号,它直接意味着和实际期望结果的差异,代表着与我们预期结果的差距,而前面的各层的误差都是从后往前传递计算的误差。
三、实验结果:
输入初始参数:
正在训练:
训练成功:
测试数据:
值得一提的是,本次课程设计仍然存在一定的不足。本次课程设计中采用的学习效率是一个定值,没有发生过改变。这样的话,在某些地方用函数逼近的时候出现了一些误差。所以,如果能够将这个学习效率能够自动调整,在一开始是一个数值比较大的学习效率,这样可以更快速地接近理想函数,等到快接近理想函数的时候,这个时候的话采用较小的学习效率,这样可以使最后的函数更加准确,这样的话训练时间会缩短,并且训练的效果会更佳。
实验一开始,采取的参数不是很合适,采取了较大的学习效率,这样导致训练失败了,一开始采取的训练次数也较低,最后的结果也是训练失败,因此,学习效率和步长都不可以太大,如果太大,波动也大了,这样的话,发散的概率提高了太多。学习效率和步长也不可以过小,如果过小,训练时间会很长,
影响性能。然后预定误差对实验的进行影响也比较大,如果预定误差值过小,则实验最后的效果会出现较大的偏差,如果预定误差值较大,则训练次数和时间会过大。
所以,在本次实验中,一定要把握好参数的设定,否则结果会很差。
四、算法分析:
设输入层神经元数量为 n1,隐藏层神经元数量为 n2,输出层神经元数量为n3。对于一个测试样本进行前馈计算,则需要进行两次矩阵运算,两次向量和矩阵相乘分别,需要进行 n1 * n2 和 n2 * n3 次计算,由于输入层神经元数量和输出层神经元数量是固定的,只有中间隐藏层的神经元数量是需要自己设定的,因此本算法时间复杂度为 O(n1 * n2 + n2 * n3) = O(n2)。
对于训练一个神经网络而言,有 k 个样本,每个样本只会被训练一次,所以训练一个神经网络的时间复杂度为 O(k*n2),同理,预测一个样本,时间复杂度是 O(n2)。对于时间复杂度,因 n1 和 n3 是固定的,即输入层与输出层神经元数量恒定,故仅相关于隐藏层神经元数量, 亦即 O(n2)。又在 n1 和 n3 恒定时,仅有 n2 随输入而波动,可知算法的一系列操作可在 O(1)的空间上完成。
为了加强鲁棒性,在满足精度要求的前提下,取尽可能少的隐层节点数,即本课程设计中的 15 个节点。
五、总结:
①首先是对隐藏层节点数目的考虑,过多或者过少都不能科学地反映出样本的规律性。如果数量太少,则不能够将训练数据的规律性概括出来。如果数量过多,也不是很好,因为可能会把一些干扰性的并不是规律的内容给记录下来,这样会使得过于准确导致某些数据还是判断失误,而且会使得训练时间变长很多。比较妥当的一个做法就是根据公式计算出一个初始的实验值。
②至于究竟是选取每输入一个样本就进行权值调整,然后计算误差,或者是输入完所有样本数据之后再进行权值调整,根据本次实验,我得出的结论是如果样本数量多的话,输入完所有样本数据之后再进行权值调整的话能更快得进行收敛。
③这次课程设计在 VC++6.0 上完成了 BP 神经网络实现的编程,明白了 BP神经网络计算过程分两步,分别是正向计算,反向计算。对于正向传播而言,计算从输入层开始到输出层结束的各层的输入输出值,对于反向传播,便是如果正向计算的输出值不满足预期,便从后往前调整权值,直至最后的数据符合预期要求。
④通过本次实验,对 BP 神经网络理解变得非常透彻,熟悉了 BP 神经网络的结构,对人工智能的应用有了一定的认识,也对数据结构的学习印象更深刻,提高了我学习相关知识的兴趣,期间遇到了很多困难,而且编程的实现对我而言比较繁琐,遇到了很多 BUG,但是都一一细心解决了。
⑤通过熟悉其数学原理,我深刻理解到了 BP 神经网络已经非常成熟。它的优点是可以解决非线性映射问题。它的网络结构也非常灵活。输入层,输出层和隐藏层的神经元数量可以根据具体的需要而设定。但是它的缺点也存在,比如说它的学习速度比较慢,就本课程设计而言,学了较大次数才能收敛,而且对于初始参数的设定而言,得不到很多的理论指导。
附录(源代码与测试文件):
源代码:
头文件necessary.h:
#include
#include
#include
#include
#include
#include
#define SampleCount 15 //学习样本个数
#define INnum 2 //输入层神经元数目
#define HN 15//隐层神经元数目
#define ONnum 1 //输出层神经元数目
using namespace std; 头文件bp.h:
#ifndef BP_H
#define BP_H
#include "necessary.h"
class Back_propagation
{
public:
Back_propagation();
double W[HN][INnum]; //输入层至隐层权值
double V[ONnum][HN]; //隐层至输出层权值
double P[INnum]; //单个样本输入数据
double T[ONnum]; //单个样本期望输出值
double OLD_W[HN][INnum]; //保存HN-IN旧权!
double OLD_V[ONnum][HN]; //保存ON-HN旧权!
double HI[HN]; //隐层的输入
double OI[ONnum]; //输出层的输入
double hidenLayerOutput[HN]; //隐层的输出
double OO[ONnum]; //输出层的输出
double err_m[SampleCount]; //第m个样本的总误差
double studyRate;//学习效率效率
double b;//步长
double e_err[HN];
double d_err[ONnum];
void input_p(int m);
void input_t(int m);
void H_I_O();
void O_I_O();
void Err_Output_Hidden(int m);
void Err_Hidden_Input();
void Adjust_O_H(int m,int n);
void Adjust_H_I(int m,int n);
void saveWV();
struct
{
double input[INnum];
double teach[ONnum];
}Study_Data[SampleCount];
private:
};
#endif源文件necessary.cpp:
#include "necessary.h"源文件bp.cpp:
#include"bp.h"
Back_propagation::Back_propagation()
{
srand( (unsigned)time( NULL ) );
for( int i = 0; i < HN; i ++ )
{
for( int j = 0; j < INnum; j ++ )
{
W[i][j] = double( rand() % 100 ) / 100; //初始化输入层到隐层的权值
}
}
for( int ii = 0; ii < ONnum; ii ++ )
{
for( int jj = 0; jj < HN; jj ++ )
{
V[ii][jj] = double( rand() % 100 ) / 100; //初始化隐层到输出层的权值
}
}
}
void Back_propagation::input_p(int m)
{
for( int i = 0; i < INnum; i ++ )
{
P[i] = Study_Data[m].input[i];
}
}
void Back_propagation::input_t(int m)
{
for( int k = 0; k < ONnum; k ++ )
{
T[k] = Study_Data[m].teach[k];
}
}
void Back_propagation::H_I_O()
{
double net;
int i,j;
for( j = 0; j < HN; j ++ )
{
net = 0;
for( i = 0; i < INnum; i ++ )
{
net += W[j][i] * P[i];//求隐层内积
}
HI[j] = net;// - Thread_Hiden[j];//求隐层输入
hidenLayerOutput[j] = 1.0 / ( 1.0 + exp(-HI[j]) );//求隐层输出
}
}
void Back_propagation::O_I_O()
{
double net;
int k,j;
for( k = 0; k < ONnum; k ++ )
{
net = 0;
for( j = 0; j < HN; j ++ )
{
net += V[k][j] * hidenLayerOutput[j];//求输出层内积
}
OI[k] = net; //求输出层输入
OO[k] = 1.0 / ( 1.0 + exp(-OI[k]) );//求输出层输出
}
}
void Back_propagation::Err_Output_Hidden( int m )
{
double abs_err[ONnum];//样本误差
double sqr_err = 0;//临时保存误差平方
for( int k = 0; k < ONnum; k ++ )
{
abs_err[k] = T[k] - OO[k]; //求第m个样本下的第k个神经元的绝对误差
sqr_err += (abs_err[k]) * (abs_err[k]);//求第m个样本下输出层的平方误差
d_err[k] = abs_err[k] * OO[k] * (1.0-OO[k]);//d_err[k]输出层各神经元的一般化误差
}
err_m[m] = sqr_err / 2;//第m个样本下输出层的平方误差/2=第m个样本的均方误差,据ppt1.5-3
}
void Back_propagation::Err_Hidden_Input()
{
double sigma;
for( int j = 0; j < HN; j ++ )
{
sigma = 0.0;
for( int k = 0; k < ONnum; k ++ )
{
sigma += d_err[k] * V[k][j];
}
e_err[j] = sigma * hidenLayerOutput[j] * ( 1 - hidenLayerOutput[j] );//隐层各神经元的一般化误差
}
}
void Back_propagation::Adjust_O_H( int m,int n )
{
if( n <= 1 )
{
for( int k = 0; k < ONnum; k ++ )
{
for( int j = 0; j < HN; j ++ )
{
V[k][j] = V[k][j] + studyRate * d_err[k] * hidenLayerOutput[j];//输出层至隐层的权值调整
}
}
}
else if( n > 1 )
{
for( int k = 0; k < ONnum; k ++ )
{
for( int j = 0; j < HN; j ++ )
{
V[k][j] = V[k][j] + studyRate * d_err[k] * hidenLayerOutput[j] + b * ( V[k][j] - OLD_V[k][j] );//输出层至隐层的权值调整
}
}
}
}
void Back_propagation::Adjust_H_I( int m,int n )
{
if( n <= 1 )
{
for( int j = 0; j < HN; j ++ )
{
for ( int i = 0; i < INnum; i ++ )
{
W[j][i] = W[j][i] + studyRate * e_err[j] * P[i];//隐层至输入层的权值调整
}
}
}
else if( n > 1 )
{
for( int j = 0; j < HN; j ++ )
{
for( int i = 0; i < INnum; i ++ )
{
W[j][i] += studyRate * e_err[j] * P[i] + b * ( W[j][i] - OLD_W[j][i] );//隐层至输入层的权值调整
}
}
}
}
void Back_propagation::saveWV()
{
for( int i = 0; i < HN; i ++ )
{
for( int j = 0; j < INnum; j ++ )
{
OLD_W[i][j] = W[i][j];
}
}
for( int ii = 0; ii < ONnum; ii ++ )
{
for( int jj = 0; jj < HN; jj ++ )
{
OLD_V[ii][jj] = V[ii][jj];
}
}
}源文件main.cpp:
#include "bp.h"
void saveWV( Back_propagation bp )
{
for( int i = 0; i < HN; i ++ )
{
for( int j = 0; j < INnum; j ++ )
{
bp.OLD_W[i][j] = bp.W[i][j];
}
}
for( int ii = 0; ii < ONnum; ii ++ )
{
for( int jj = 0; jj < HN; jj ++ )
{
bp.OLD_V[ii][jj] = bp.V[ii][jj];
}
}
}
//保存数据
void savequan( Back_propagation bp )
{
ofstream outW( "w.txt" );
ofstream outV( "v.txt" );
for( int i = 0; i < HN; i ++ )
{
for( int j = 0; j < INnum; j ++ )
{
outW << bp.W[i][j] << " ";
}
outW << "\n";
}
for( int ii = 0; ii < ONnum; ii ++ )
{
for( int jj = 0; jj < HN; jj ++ )
{
outV << bp.V[ii][jj] << " ";
}
outV << "\n";
}
outW.close();
outV.close();
}
double Err_Sum( Back_propagation bp )
{
double total_err = 0;
for ( int m = 0; m < SampleCount; m ++ )
{
total_err += bp.err_m[m];//每个样本的均方误差加起来就成了全局误差
}
return total_err;
}
int main()
{
double sum_err;
int study;
int m;
double check_in, check_out;
ifstream Train_in( "trainin.txt", ios::in );
ifstream Train_out( "trainout.txt", ios::in );
if( ( Train_in.fail() ) || ( Train_out.fail() ) )
{
//printf( "Error input file!\n" );
cerr << "Error input file!" << endl;
exit(0);
}
Back_propagation bp;
cout << "请输入学习效率: studyRate = ";
cin >> bp.studyRate;
cout << "\n请输入步长: b= ";
cin >> bp.b;
study = 0;
double Pre_error ; //预定误差
cout << "\n请输入预定误差: Pre_error = ";
cin >> Pre_error;
int Pre_times;
cout << "\n请输入预定最大学习次数:Pre_times=";
cin >> Pre_times;
for( m = 0; m < SampleCount; m ++ )
{
for( int i = 0; i < INnum; i ++ )
{
Train_in >> bp.Study_Data[m].input[i];
}
}
cout << endl;
for( m = 0; m < SampleCount; m ++ )
{
for( int k = 0; k < ONnum; k ++ )
{
Train_out >> bp.Study_Data[m].teach[k];
}
}
cout << endl;
do
{
++ study;
if( study > Pre_times )
{
cout << "训练失败!" << endl;
break;
}
for ( int m = 0; m < SampleCount; m ++ )
{
bp.input_p(m); //输入第m个学习样本 (2)
bp.input_t(m);//输入第m个样本的教师信号 (3)
bp.H_I_O(); //第m个学习样本隐层各单元输入、输出值 (4)
bp.O_I_O();
bp.Err_Output_Hidden(m); //第m个学习样本输出层至隐层一般化误差 (6)
bp.Err_Hidden_Input(); //第m个学习样本隐层至输入层一般化误差 (7)
bp.Adjust_O_H(m,study);
bp.Adjust_H_I(m,study);
if( m == 0 )
{
cout << bp.V[0][0] << " " << bp.V[0][1] << endl;
}
}//全部样本训练完毕
sum_err = Err_Sum(bp); //全部样本全局误差计算 (10)
bp.saveWV();
}while( sum_err > Pre_error );
if( ( study <= Pre_times ) & ( sum_err < Pre_error ) )
{
cout << "训练结束!" << endl;
cout << "你已经学习了 " << study << "次" << endl;
}
double net;
int k, j;
while(1)
{
printf( "请输入蠓虫的触角及翅膀的长度:" );
cin >> check_in;
cin >> check_out;
bp.P[0] = check_in;
bp.P[1] = check_out;
bp.H_I_O();
for ( k = 0; k < ONnum; k ++ )
{
net = 0;
for( j = 0; j < HN; j ++ )
{
net += bp.V[k][j] * bp.hidenLayerOutput[j];//求输出层内积
}
bp.OI[k] = net; //求输出层输入
bp.OO[k] = 1.0 / ( 1.0 + exp(-bp.OI[k]) );//求输出层输出
}
if( bp.OO[0] > 0.5 )
{
printf( "该蠓虫是af!\n" );
}
else if( bp.OO[0] >= 0 )
{
printf( "该蠓虫是apf!\n" );
}
}
return 0;
}注:题目里面既有“螨(音mǎn)虫”,也有“蠓(音měng)虫”,程序里面用的是“蠓虫”。
测试文件:
文件trainin.txt:
1.24 1.27
1.36 1.74
1.38 1.64
1.38 1.82
1.38 1.90
1.40 1.70
1.48 1.82
1.54 1.82
1.56 2.08
1.14 1.82
1.18 1.96
1.20 1.86
1.26 2.00
1.28 2.00
1.30 1.96文件trainout.txt:
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
参考文献:
[1]甘刚.BP算法在IDS中应用与实现的研究[J].成都:电子科技大学,博硕学位论文,2005.
查重结果: