数据挖掘笔记(3)-数据预处理

数据预处理的主要内容包括数据清洗、数据集成、数据变换和数据规约，它的工作量在数据挖掘过程中占60%。

4.1数据清洗

4.1.1缺失值处理

• 删除记录

• 不处理

• 数据插补

  • 使用均值/中位数/众数插补
  • 使用固定值插补
    比如男生身高这个属性有空值，可以用全国的男生平均身高来插补，这是一个固定值。
  • 最近临插补
    用与有空值的样本最接近的样本的属性值来插补。比如可以和K_means算法一样求距离，求出距离含有空值的样本最近的那个样本，用其属性值来插补空值。
    注：如果含有空值无法计算距离，可以先插补这个属性的均值
  • 回归方法
    将含有空值的属性记做y，将没有空值的其他属性记做x(x1,x2…xn),然后建立拟合模型来预测y的值。
  • 插值法

    • 拉格朗日插值法
      
      
      利用已知的n个点对建立拉格朗日插值多项式，将缺失值对应的x带入插值函数得到近似值L(x)。

    • 牛顿插值法
      当点对的数量变化时，拉格朗日插值多项式的每一项都要变化，在实际计算中很不方便，所以提出了牛顿插值法。
      (x1,y1)，(x2,y2)，(x3,y3)…(xn,yn)n个点对的一阶到n阶的差商公式如下：
      
      其中y1=f(x1)，y2=f(x2)…yn=f(xn)
      
      将缺失值对应的点x带入牛顿插值多项式得到缺失值的近似值f(x)。可见点对数量变化时牛顿插值多项式只用在后部分增加或删除就可以了。
      代码如下：

# -*- coding:utf-8 -*-
# 牛顿插值多项式


def get_n_diff_quo(xi, fi):
    """
    计算n阶差商(difference quotient)
    """
    if len(xi) > 2:
        return (get_n_diff_quo(xi[:len(xi)-1], fi[:len(fi)-1])-get_n_diff_quo(xi[1:len(xi)], fi[1:len(fi)]))/(xi[0]-xi[-1])
    return (fi[0]-fi[1])/(xi[0]-xi[1])


def get_w(xi):
    """
    计算差商前面的系数
    """
    def w(x):
        result = 1.0
        for i, j in enumerate(xi, start=1):
            # 跳过xi的最后一项
            if i == len(xi):
                break
            # print(j)
            result *= (x - j)
        return result
    return w


def get_newton_interpolate(xi, fi):
    """
    :param xi: xi存放点对的x坐标
    :param fi: fi存放点对的y坐标
    :return: 牛顿插值函数
    """
    def newton_interpolate(x):
        result = fi[0]
        for i in range(2, len(xi)+1):
            result += (get_n_diff_quo(xi[:i], fi[:i]) * get_w(xi[:i])(x))
        return result
    return newton_interpolate

if __name__ == '__main__':
    train_x = [i for i in range(-10, 11)]
    train_y = [i**2 for i in train_x]
    newton_inter = get_newton_interpolate(train_x, train_y)
    test_x = [i for i in range(11, 20)]
    predict_y = [newton_inter(i) for i in test_x]
    print(predict_y)

4.1.2异常值处理

• 删除含有异常值的记录
  当训练数据量较大时，可以删除少量含有异常值的样本。如果数据量少则该方法不可取，因为可能导致建立的模型欠拟合。
• 视为缺失值
  将异常值视为缺失值，然后用处理缺失值的方法来处理异常值。
• 平均值修正
  用前后两个观测值的均值来修正该异常值。
• 不处理
  如果该异常数据是正确数据，那么就不处理，直接用这些数据建模。因为异常数据的判断是根据数据的总体分布情况来判断，所以异常数据有可能是正常数据。比如，节假日时饭店的营销额肯定比平常时的多，所以就有可能判断它为异常数据。

4.2数据集成

数据挖掘所需要的数据往往来自不同的数据源，数据集成就是将多个的数据源合并存放在一个一致的数据存储(数据仓库)中的过程。

4.21实体识别

• 同名异义
  例如数据源A和数据源B中都有ID这个属性，但是表达的意思不一样，这时就可以更换数据源A或者数据源B中ID这个属性的名称，然后再把A、B这两个数据源整合到一起。
• 异名同义
  数据源A和数据源B中有两个属性表达的是相同的意思，但是属性名称不同，这时可以删除A或B中的该属性，只保留一个即可，然后再把A、B这两个数据源整合到一起。
• 单位不统一
  将多个数据源中描述得是同一个实体但使用的计量单位不同的属性，只保留一份该属性，避免数据冗余。

4.2.2冗余属性识别

• 同一属性出现多次
  直接删除冗余属性，只保留一份即可。
• 表达的意思相同但命名不一致的属性出现多次
  可先对两个属性进行相关性分析，确定是冗余属性再将其删除。

4.3数据变换

数据变换是对数据进行规范化处理，将数据转换成“适当的”形式，以适用于挖掘任务和算法的需要。

4.3.1简单的函数变换

通常对原始数据进行一些比较简单的函数变化，比如平方、开方、取对数或者差分运算。比如人的个人年收入10000元到10亿元，可以通过取对数压缩年收入的取值区间，方便完成数据挖掘任务。

4.3.2数据规范化

• 最大-最小规范化
  最大-最小规范化也称离差规范化，可以将原始数据映射到[0, 1]区间内。离差标准化保留了原始数据之间的关系，是消除量纲和数据取值范围影响的最简单的方法。
  变换公式如下：
  
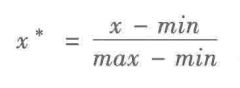
  缺点：如果最大值max的值很大，会导致变换后的数据都接近于0，并且相差不大。

• 中心化(零均值化)
  对原始数据进行中心化，使得中心化后的数据均值为0。
  变换公式如下：
  

• 标准差标准化
  对原始数据进行数据标准化，标准化后的数据均值为0，方差为1。这是使用的最多的数据规范化处理的方法。
  变换公式如下：
  
  x拔为均值，西格玛为标准差。

• 小数定标规范化
  通过移动原始数据的小数点的位置，将原始数据映射到[-1, 1]区间内，小数点移动的位数取决于原始数据中绝对值的最大值。
  变换公式如下：
  
  k=np.ceil(np.log10(data.abs().max()))，k为原始数据中绝对值的最大值对10取对数然后上取整得到。

4.3.3连续属性离散化

比如决策树算法，它需要每个属性的取值是有限个(也就是离散的)，这样就可以选个最优的属性利用属性值来划分数据集。如西瓜数据集，按照西瓜的色泽属性(该属性取值有黑色、青绿色和浅白色)可以将数据集划分为黑色瓜，青绿色瓜和浅白色瓜。但是如果按照西瓜的含糖率属性(这是一个连续属性)无法根据它的取值来划分数据集，这时可以将连续属性离散化，比如选择一个划分点0.5，将含糖率>0.5和含糖率<0.5作为含糖率属性的取值。

常用的离散化方法如下：

• 等宽法
  将属性的值域分成若干个等宽度的区间，区间的个数根据具体的数据集来定。这若干个等宽度的区间就是该连续属性的离散取值。
  缺点：如果原始数据分布本来就不均匀，可能存在某个区间是空区间，这严重损坏建立的模型。
• 等频法
  将属性的值域分成若干个不同的区间，要求每个区间包含的数据量的个数是相同的即等频。
  缺点：为了使每个区间包含的数据量的个数是相同的，可能将相同的数据分到不同的区间来满足这个要求，这会影响模型建立。
• 聚类
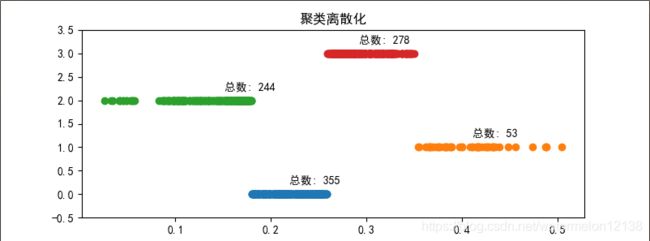
  对连续属性的值使用聚类算法得到若干个簇，将合并到一个簇内的连续属性值做同一标记。簇的个数需要人为指定，这若干簇将作为该连续属性的离散取值。

例子：

# -*- coding: utf-8 -*-
# 连续属性离散化
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans  # 引入KMeans

datafile = 'F:/DataMining/chapter4/discretization_data.xls'
data = pd.read_excel(datafile)  # 读取数据
data = data['肝气郁结证型系数'].copy()
print('data: \n', data)

# 等宽离散化，各区间依次命名为0,1,2,3
k = 4
d1 = pd.cut(data, k, labels=range(k))
print('d1: \n', d1)


# 等频率离散化
w = [1.0*i/k for i in range(k+1)]
print('w: \n', w)
print('describe: \n', data.describe())
print(type(data.describe()))
# data.describe()得到的结果类型是Series，它的前4行分别计算了count、mean、std、min
# 从第五行开始计算分位数，[4:4+k+1]取出计算出来的分位数
quantiles = data.describe(percentiles=w)[4:4+k+1]
print('quantiles: \n', type(quantiles))
# 0%分位数就是最小值，100%分位数就是最大值
print(data.min())
print(data.max())
# include_lowest=True, right=False表示左闭右开
# 如quantiles=[a, b, c, d]，那么将按照[a, b)、[b,c)、[c,d)来划分数据集data
d2 = pd.cut(data, quantiles, include_lowest=True, right=False, labels=range(k))
print('d2: \n', d2)


# 聚类离散化
# 建立模型，n_jobs是并行数，一般等于CPU数较好
kmodel = KMeans(n_clusters=k, n_jobs=1)
# 训练模型
# data为DataFrame格式的，可以直接转换为数组格式
# KMeans需要的数组或者矩阵格式的训练数据，每行表示一个样本，每列表示一个特征
kmodel.fit_predict(np.array(data).reshape(-1, 1))

# kmodel.labels_可以查看每个样本的聚类标签,以数组格式1行n列返回
# print('kmodel.labels_: \n', kmodel.labels_)
# 将1行n列的数组或者一个列表转换成category格式的数据
d3 = pd.Series(data=kmodel.labels_, dtype='category')
print('d3: \n', d3)


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
titles = ['等宽离散化', '等频率离散化', '聚类离散化']


def cluster_plot(d, t, k):   # 自定义作图函数来显示聚类结果
    plt.figure(figsize=(8, 3))
    for j in range(k):
        plt.plot(data[d == j], [i for i in d[d == j]], 'o')
        # 添加注释，标明每个区间的数据个数
        tmp = np.array(data[d == j])
        tmp.sort(axis=0)
        plt.annotate('总数: %d' % len(tmp), xy=(tmp[len(tmp)//2], j+0.2))
    plt.ylim(-0.5, k-0.5)
    plt.title(t)
    return plt

cluster_plot(d1, titles[0], k).show()
cluster_plot(d2, titles[1], k).show()
cluster_plot(d3, titles[2], k).show()

结果展示：

4.3.4属性构造

利用已有属性构造新的属性。比如已知一定时期内人口的平均数，出生人口数和死亡人口数我们可以得到新的属性出生率和死亡率。

4.4数据规约

在庞大的数据集上进行数据分析和数据挖掘是一件复杂且耗时的任务，数据规约可以产生较小而且保持原数据集完整性的新数据集，在新数据集上进行数据分析和数据挖掘将更有效率。
优点如下：
(1)降低错误、无效数据对建模的影响
(2)降低数据存储的成本
(3)少量且具有代表性的数据集大幅缩减了数据挖掘的时间

4.4.1属性规约

• 合并属性
  将多个旧属性合并成一个更具效率的新属性。
• 逐步向前选择
  从一个空属性集开始，每次从原属性集中选择一个最优的属性添加到当前属性集中，直到选择不出最优的属性或者达到阈值约束为止。
  “如何判断最优”
• 逐步向后删除
  每次从原属性集中选择一个最差的属性删除，直到选择不出最差的属性或者达到阈值约束为止。
  “如何判断最差”
• 决策树归纳
  在原属性集上建立一棵决策树，将没有出现在这棵决策树上的属性删除。可以得到一个较优的属性子集。
• 主成分分析(PCA)
  主成分分析是一种适用于连续属性的数据降维方法，它构造了原始数据的正交变换，新空间的基底去除了原始空间基底的相关性，使得用较少的变量就可以解释原始数据中的大部分变量。
  算法原理：请点这里
  算法流程：
  (1)假设原始数据为m个样本，每个样本有n个特征，将原始数据组成m行n列的矩阵X。
  (2)对矩阵X按列进行中心化，记中心化后的矩阵仍为X。
  (3)求中心化后的矩阵X的协方差矩阵C。
  C等于X的转置乘X
  (4)计算矩阵C的特征值和特征向量
  (5)将矩阵C的特征值按从大到小的顺序排列，取出前k个特征值所对应的特征向量按列摆放组成矩阵P，P为n行k列。
  如何确定k：通过方差百分比确定k。
  
  (6)原始矩阵X乘以矩阵P得到降维后的矩阵。

4.4.2数值规约
数值规约通过选择较小的、替代的数据来较少数据量，包括有参方法和无参方法。

• 无参方法
  • 直方图
    有点像连续属性的离散化，但对于离散属性也同样适用，也是将多个数据划分区间，将划分后的区间作为这个属性的取值，这样数据量就会减少。
    例子：
    某餐厅的菜品单价表如下：
    
    划分区间并建立直方图：
    
    菜品单价属性就不用存放多个数据，只需存放这三个区间。
    • 抽样
      假设原始数据集D包含N个元组，每一行可以视为一个元组，采用抽样方法可减小数据集。用抽样得到的子集来代替原数据集。
      抽样方法可取：
      (1)无放回抽样
      (2)有放回抽样
      (3)分层抽样
      将原始数据集D分成互不相交的几个部分，称作层，对每一层进行简单随机抽样可以得到D的分层样本。
      比如某饭店的顾客数据集，可以通过年龄将D分层，再对每一层进行抽样。
• 有参方法
  有参方法使用一个模型来描述数据，只需存放模型的参数而不存放真实的数据，
  线性模型(线性回归等)和对数线性模型可以很好的评估数据。
  例子：
  对某个属性的取值建立线性回归模型，这时属性的取值就只需存放线性回归模型的参数即斜率和截距，而不用存放各种各样的数据。

4.5 数据预处理常用的函数

(1) unique()

(2) isnull()/notnull()

(3) cut()

# def cut(x, bins, right=True, labels=None, retbins=False, precision=3,
#         include_lowest=False, duplicates='raise'):
# x:支持一维数据如array、series、list等
# bins: 支持int或数字序列。
#        * int: 如bins为int型k，则将数据x分为k个等宽的区间。区间长度：(x.max()-x.min())/k
#        * 数字序列：如bins为list=[2, 20, 34, 50]，则将x为(2,20]、（20, 34]、（34, 50]三个区间
# labels：支持数组或列表，也可以为bool类型，也可以不写
#        * 数组或列表：如labels=['a', 'b', 'c']，bins返回的第一个区间内的所有数据的标签都是'a'
#                      返回的第二个区间内的所有数据的标签都是'b',返回的第二个区间内的所有数据的标签都是'c'
#        * bool: 如labels=False，则bins返回的第一个区间内的所有数据的标签都是'0'
#                                返回的第二个区间内的所有数据的标签都是'1',以此类推
#        * 不写：返回的是每个数据所在的区间
# retbins: 支持bool类型默认为False。retbins=True则在print()的时候返回划分的所有区间
# right=True: 划分后的所有区间默认为右闭区间
# include_lowest=False ：第一个区间是否为左闭区间默认为否

代码展示：
原始数据data如下：

cut_data = pd.cut(df['col1'], 4, labels=False)
print('cut_data: \n', cut_data)
结果如下：

注1：要获取每个数据所在的区间应该不写labels。
注2：如只需获取划分后的区间，retbins=True。