【leetcode刷题班】贪心题目求解
leetcode455、分糖果(easy)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有一个尺寸 sj 。如果 sj >= gi ,我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
注意:
你可以假设胃口值为正。
一个小朋友最多只能拥有一块饼干。
输入: [1,2,3], [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。1.对需求因子数组g与糖果大小数组s进行从小到大的排序。
2.按照从小到大的顺序使用各糖果尝试是否可满足某个孩子,每个糖果只尝试1次;若尝试成功,则换下一个孩子尝试;直到发现没更多的孩子或者没更多的 糖果,循环结束。
# 贪心算法
class Solution(object):
def findContentChildren(self, g, s):
g = sorted(g) # 需求
s = sorted(s) # 糖果
child = 0 # 已满足几个孩子
cookie = 0 # 尝试了几个糖果
while cookie < len(s) and child < len(g): # 要么孩子用光了,要么糖果用光了
if g[child] <= s[cookie]:
child += 1
cookie += 1
return childleetcode375、摇摆序列(medium)
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。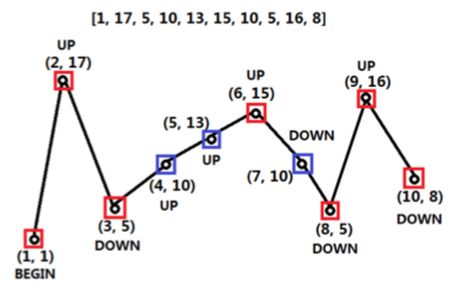 在(4,10)的时候max_length++,(6,15)的时候没有++。
在(4,10)的时候max_length++,(6,15)的时候没有++。
在连续递增、递减的时候,选择最大的。
leetcode402、移除k个数字(medium)
给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小。
注意:
- num 的长度小于 10002 且 ≥ k。
- num 不会包含任何前导零。
示例 1 :
输入: num = "1432219", k = 3 输出: "1219" 解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
