MATLAB/Simulink在控制系统仿真与CAD应用(二)
MATLAB控制系统仿真
- Simulink系统仿真部分
- 仿真微分方程
- 仿真非线性系统
- 基于常用非线性模块组合搭建非线性环节
- 任意单值非线性环节查表模块实现
- 多值非线性环节搭建
- 由Simulink仿真框图推导微分方程组并比对
- 使用Simulink Linear Analysis Tool分析系统
- Simulink + fminsearch/fmincon 控制器参数整定
- LTI模型的使用
- 非线性系统线性化
- Simulink S-函数编写与应用
- Fcn模块的使用(时变系统仿真)
- Simulink模型预置参数
- Smith预估模型
Simulink系统仿真部分
仿真微分方程
y ( 4 ) + 5 y ( 3 ) + 6 y ′ ′ + 4 y ′ + 2 y = e − 3 t + e − 5 t s i n ( 4 t + π / 3 ) y^{(4)}+5y^{(3)}+6y''+4y'+2y=e^{-3t}+e^{-5t}sin(4t+\pi/3) y(4)+5y(3)+6y′′+4y′+2y=e−3t+e−5tsin(4t+π/3)
f=@(t,x)[x(2);x(3);x(4);exp(-3*t)+exp(-5*t)*sin(4*t+pi/3)-5*x(4)-6*x(3)-4*x(2)-2*x(1)];
x0=[1;1/2;1/2;0.2];
tf=30;
[t,x]=ode45(f,[0,tf],x0);
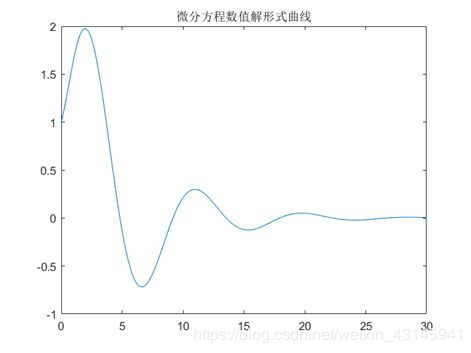
figure;plot(t,x(:,1));title('微分方程数值解形式曲线')
仿真非线性系统
基于常用非线性模块组合搭建非线性环节
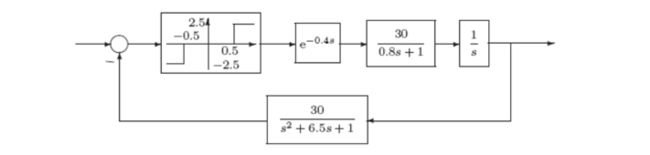
注意:
图中的非线性饱和环节是由两个relay原件并联构成,把其参数设置成下面这样:
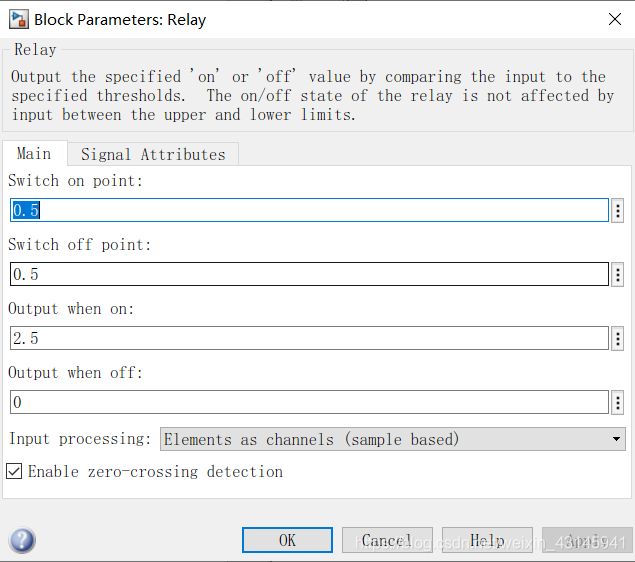
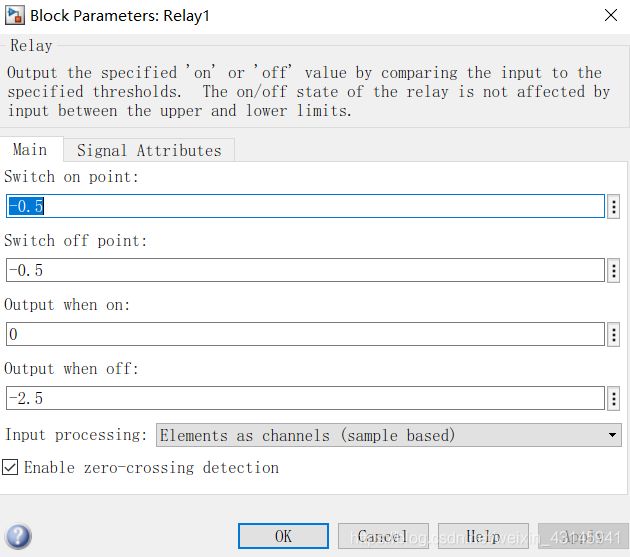

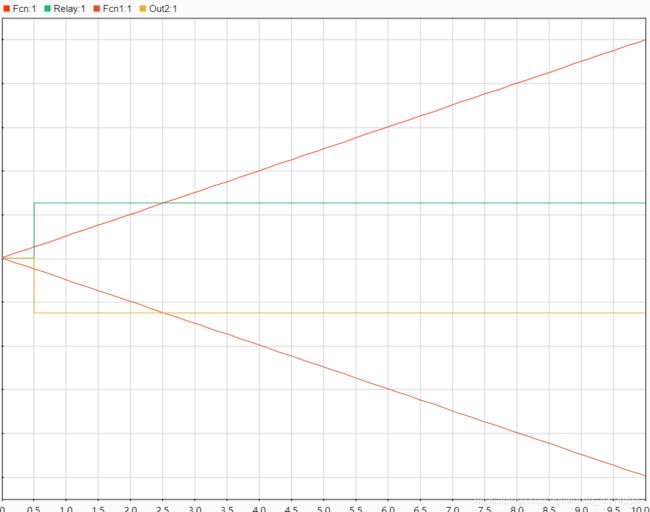
由图我们可以看出将它们并联就能得到我们想要的环节了(并联图像相加)
任意单值非线性环节查表模块实现
在实际仿真控制系统的时候,非线性环节往往难以用Discontinuities中模块组合得到,并且就算能组合,工作量也大,因此我们给出任意单值非线性环节的实现方法。
考虑如下非线性环节:
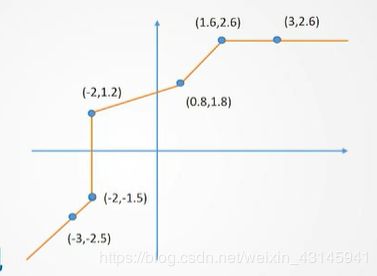
使用查表模块:Lookup Tables——1-D lookup Table
首先在工作空间输入对应的横纵坐标:
xx=[-3 -2 -2+eps 0.8 1.6 3];
yy=[-2.5 -1.5 1.2 1.8 2.6 2.6];
注意eps的使用,因为这个非线性在-2处实际上是多值的。另外键入数据的时候非线性环节首尾应分别给出一个延长线上的点的坐标。
之后双击模块输入对应数组名就能得到我们想要的非线性环节:
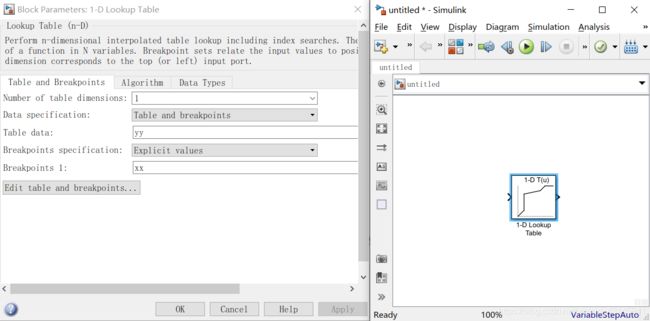
多值非线性环节搭建
常见的多值非线性环节就是滞回特性曲线,我们考虑将它分为两个单值非线性,分出来的两个图像分别是x上升和x下降时所用的图像。

下面的问题就是如何判断输入到底在上升还是下降,以及switch模块的使用,我们给出下面搭建好的模型加以说明。
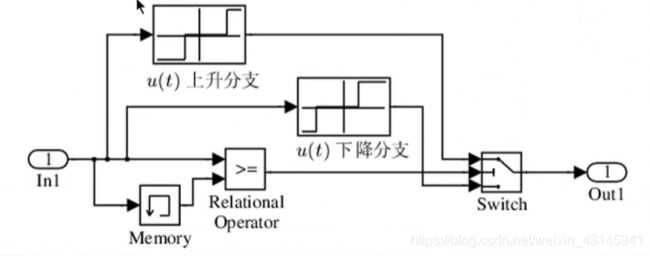
Memory的输出是仿真时刻上一时刻的输入值,通过Relational operator比较大小后控制Switch开关切换两个分支,而这两个分支就是由单值非线性查表模块搭建的。
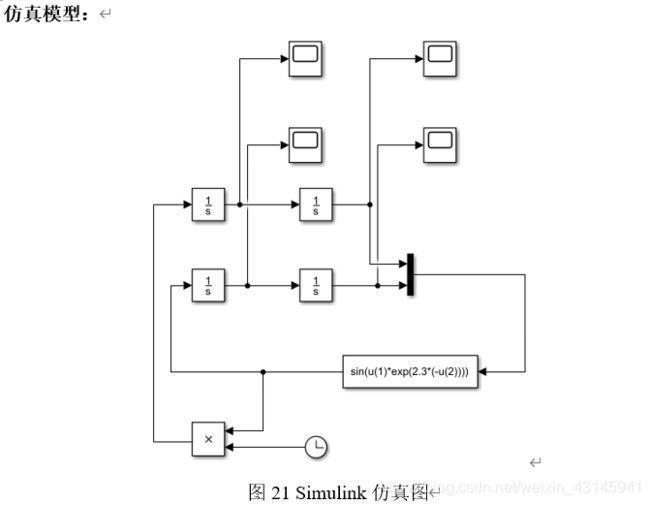
由Simulink仿真框图推导微分方程组并比对

显然有如下式子:
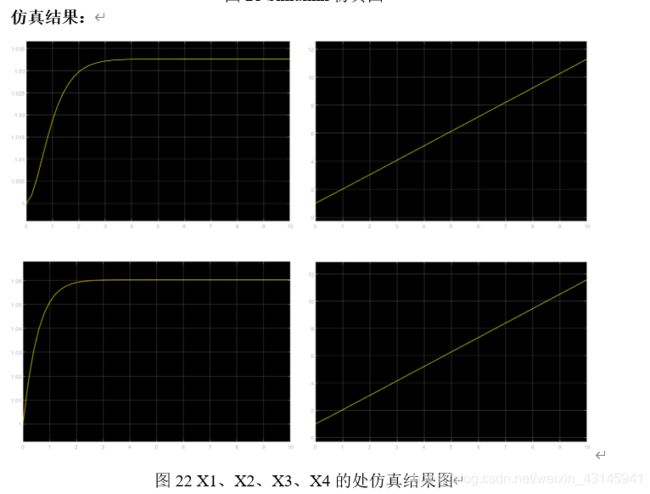
x 1 ˙ = t s i n ( x 2 e − 2.3 x 4 ) x 2 ˙ = x 1 x 3 ˙ = s i n ( x 2 e − 2.3 x 4 ) x 4 ˙ = x 3 \dot{x_1}=tsin(x_2e^{-2.3x_4})\\\dot{x_2}=x_1 \\\dot{x_3}=sin(x_2e^{-2.3x_4})\\\dot{x_4}=x_3 x1˙=tsin(x2e−2.3x4)x2˙=x1x3˙=sin(x2e−2.3x4)x4˙=x3
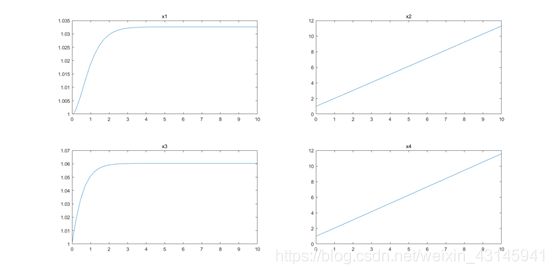
f=@(t,x)[t*sin(x(2)*exp(2.3*(-x(4))));x(1);sin(x(2)*exp(2.3*(-x(4))));x(3)];
[t,y]=ode45(f,[0,10],[1,1,1,1]);
subplot(2,2,1);plot(t,y(:,1));title('x1');
subplot(2,2,2);plot(t,y(:,2));title('x2');
subplot(2,2,3);plot(t,y(:,3));title('x3');
subplot(2,2,4);plot(t,y(:,4));title('x4');
使用Simulink Linear Analysis Tool分析系统
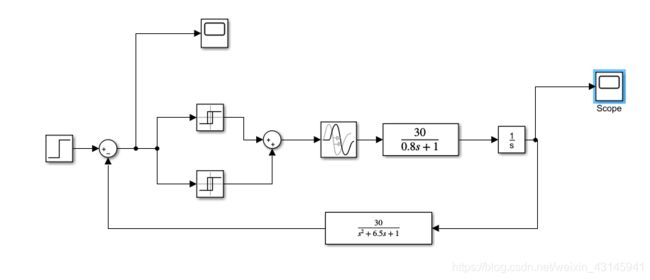
首先我们建立一个简单的闭环系统:
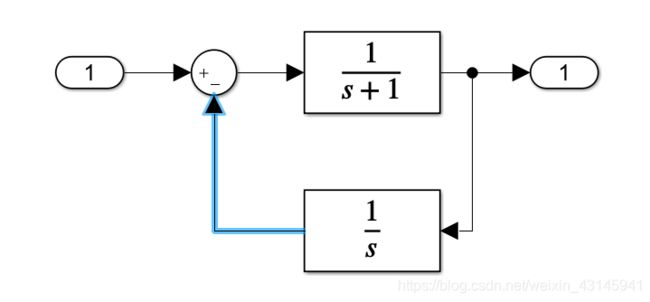
打开如下菜单:
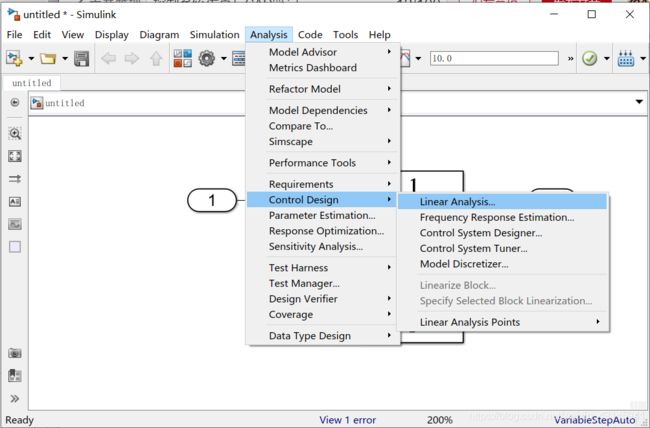
点击Create New
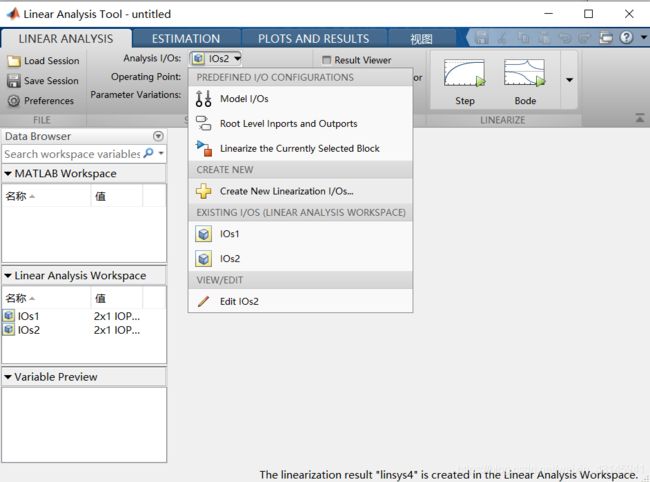
用鼠标选中你想分析的输入输出信号线,加入。输入的配置不用动,输出的改成Output Measurement。
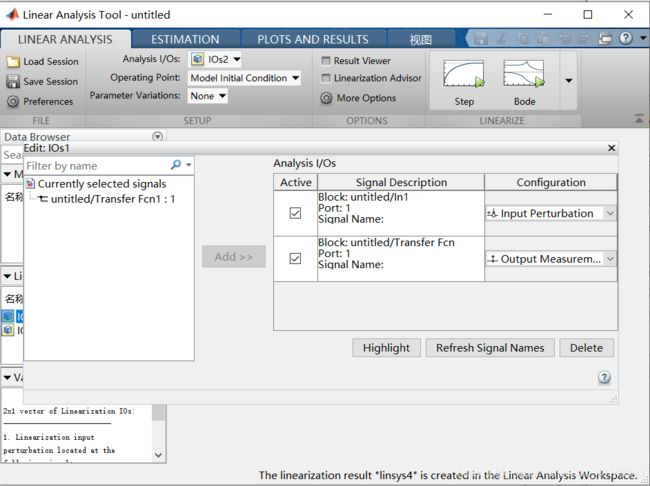
然后即可开始分析,如果分析开环,信号线就要选到闭环内开环线上,如果分析闭环则选在系统外,否则Bode图不对应。
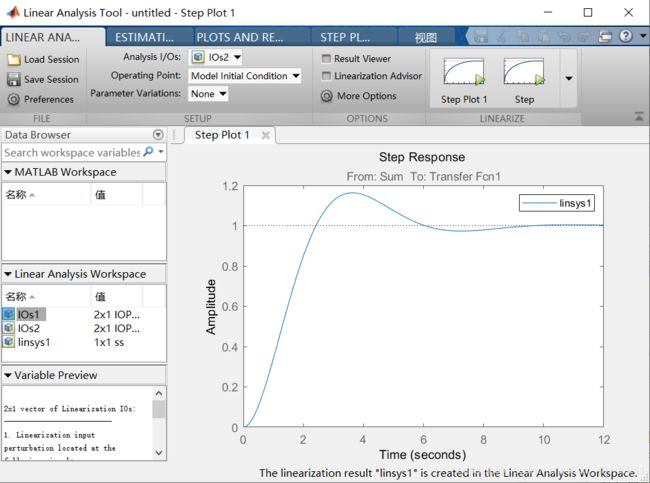
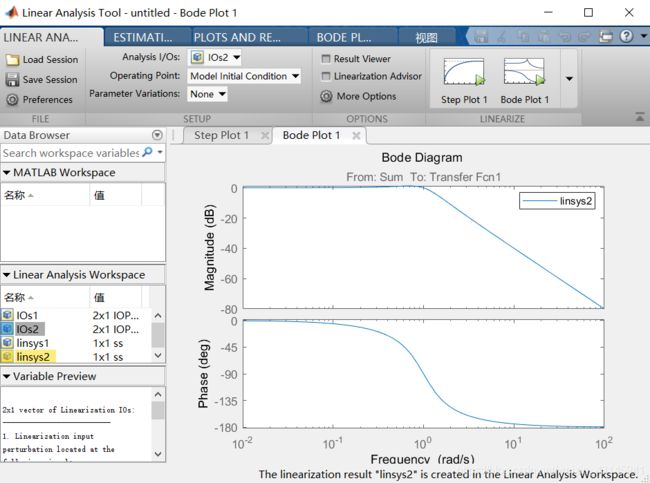
使用该工具线性化系统
需要在模型输入输出线上右键将其设置为Input 和 output measurement,然后进工具箱:
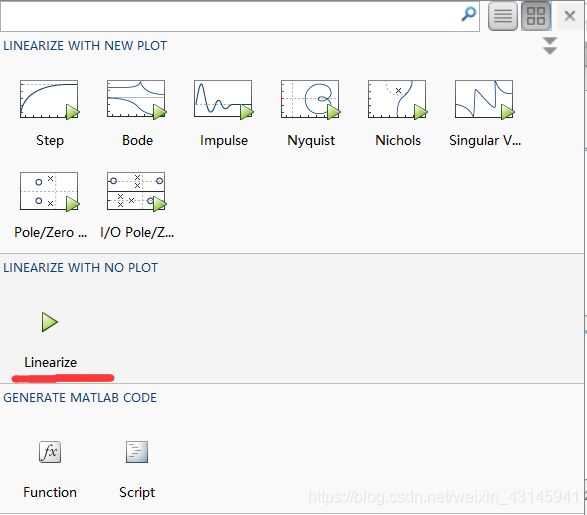
然后点击:

然后选择模型的不同表达方式:
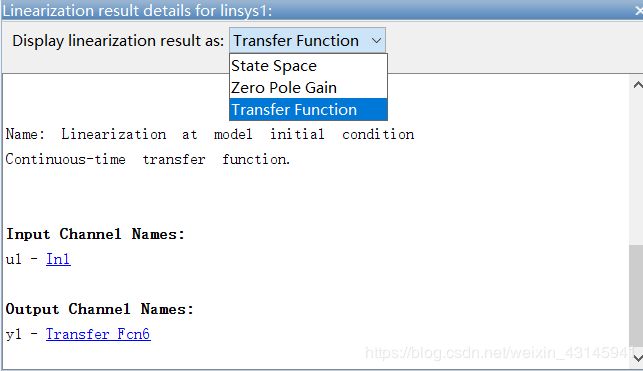
Simulink + fminsearch/fmincon 控制器参数整定
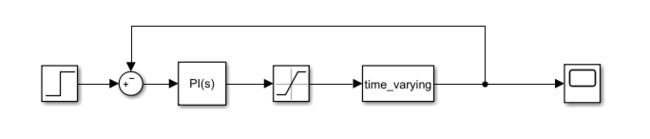
- 用Simulink搭建控制系统。下面以一个PID控制系统为例演示。
如图所示:
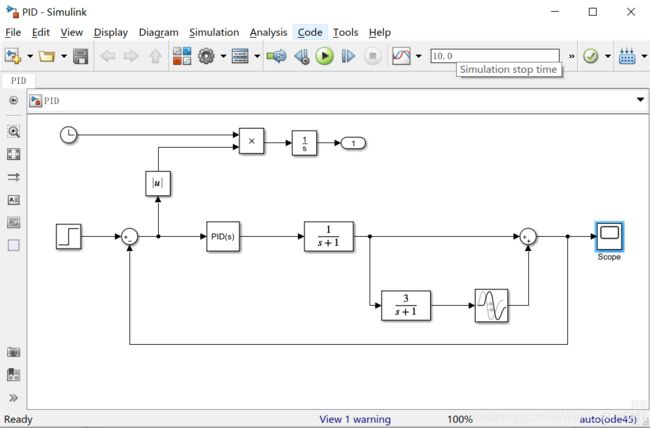
我们衡量一个控制器好坏自然想到的是响应过程中误差对时间的积分,但是这个积分形式有很多种,例如:
J I S E = ∫ 0 ∞ e 2 ( t ) d t J_{ISE}=\int_0^\infty e^2(t)dt JISE=∫0∞e2(t)dt
J I A E = ∫ 0 ∞ ∣ e ( t ) ∣ d t J_{IAE}=\int_0^\infty |e(t)|dt JIAE=∫0∞∣e(t)∣dt
J I T A E = ∫ 0 ∞ t ∣ e ( t ) ∣ d t J_{ITAE}=\int_0^\infty t|e(t)|dt JITAE=∫0∞t∣e(t)∣dt
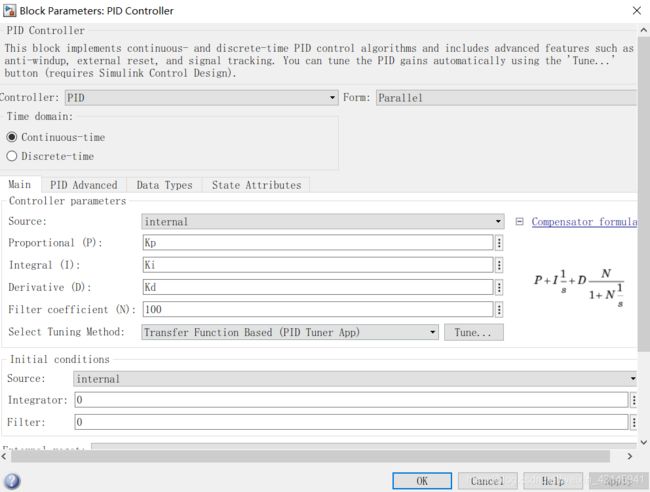
我们选用ITAE指标,因为这个指标用时间加权误差,迫使误差在时间稍大时强行减小。 - PID控制器参数设置
因为我们需要从外部.m输入PID参数,因此我们需要在Simulink中先设置三个工作空间参数。
- 编写.m文件
实时脚本:
x=fminsearch(@c7fopt3,[1 1 1])
function y=c7fopt3(x)
assignin('base','Kp',x(1));%将x(1)存到工作区间‘Kp’变量
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));
[t,~,yy] = sim('PID',[0,30]);
y = yy(end,1);
end
sim函数的返回值为时间、状态、输出矩阵。因为我们的输出是一个随时间的积分,仿真时间是30s,因此每一次sim都会返回一个自变量是时间,因变量是每一刻时间的积分值,但是我们关心的30s结束后最终的积分值,因此我们返回yy的最后一个数。
这里之所以用assignin是因为函数只能对局部变量进行赋值,想要把值赋给全局变量Kp、Ki、Kd就需要这个函数实现,如果在脚本中想对Simulink中模型变量赋值就可以直接使用等号赋值。
将Simulink中示波器点开,.m文件运行。
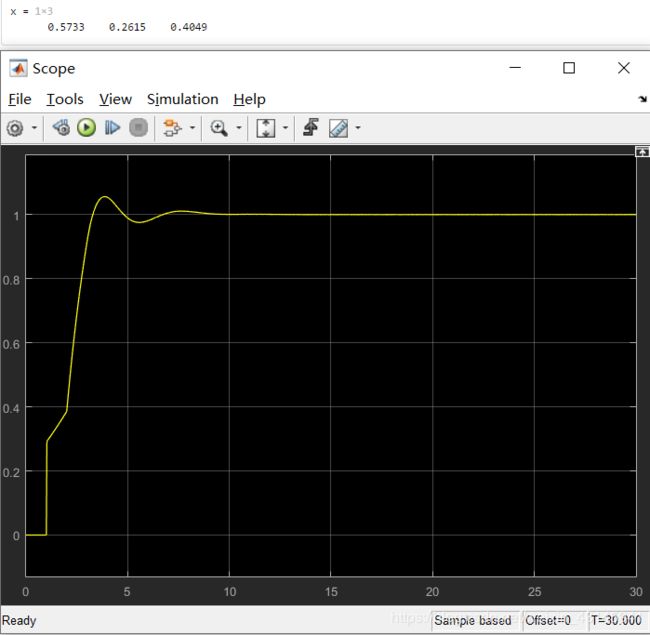
可以看出,控制效果比较不错。
LTI模型的使用
在Simulink环境下搭建模型虽然直观但是比较耗时,以多变量传递函数为例,在Simulink下需要调用很多子模块来搭建。而MATLAB工作空间搭建传递函数矩阵就显得更加快速方便,因此我们考虑在工作空间通过代码方式搭建模型后传入Simulink环境,这时就需要使用LTI模块,双击LTI模块将传递函数设置成已经通过代码搭建好的模型名称。(这个模块建议直接搜索‘LTI System’,不好找。)
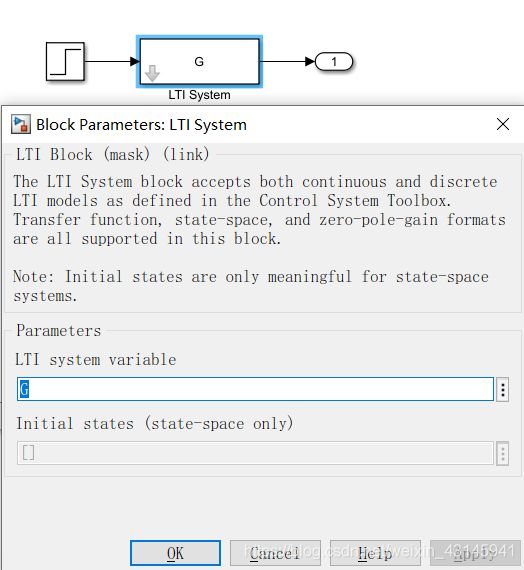
这时再从外部简单搭建一些其他模块就可以了,在仿真复杂系统的时候这会让界面更加简洁直观。
非线性系统线性化
这里我们拿一个双闭环直流调速的例子做演示:
首先搭建Simulink模型,注意如果要在工作空间调用线性化函数需要给出输入输出端子。
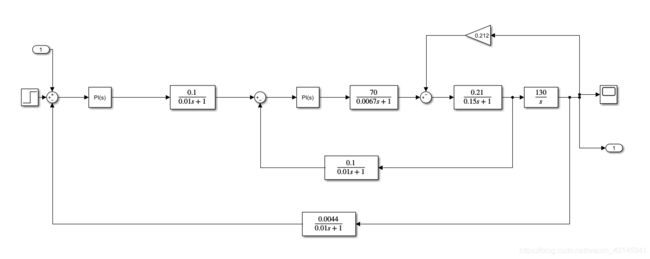
使用linearize函数线性化,虽然这个双闭环系统本身就是线性的,但是我们只是用这个例子来演示,对于非线性程度不高的非线性系统也是能用的,但是经过我的测试它对延时项是不做处理的,也就是step给的1s纯滞后但是线性化后的模型是不带滞后的,然而阶跃响应形状相同。
G = linearize('shuagnbihuan')
G1 = zpk(G);
G2 = minreal(G1,1e-1);
[t,x,y] = sim('shuagnbihuan');
[y1,t1] = step(G1);
plot(t1,y1,t,y)
G1系统中存在零极点对消的情况,因此我们对系统做最小实现处理(minreal)。
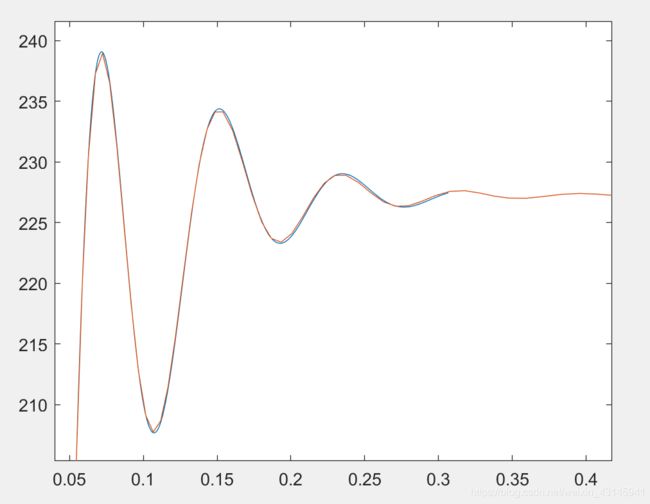
可以看出模型近似效果非常好,几乎看不出差别。
Simulink S-函数编写与应用
一开始接触Simulink的同学可能对Simulink的工作机制感到困惑,其实Simulink下大部分模块都是用S函数编写的,当然也有M函数,但是M函数是一个静态的函数,S函数跟像一个具有惯性的状态空间,拥有自己的状态变量,当你有能力熟练编写S函数的时候,你对Simulink的理解会提升一个水平。下面我们用一个比较简单的例子来自己编写一个模块。
搭建模块:中值滤波器
在这之前我也搭过LMS自适应滤波器,只是LMS算法有一个比较迷的地方就是那个理想输出的问题,所以在这我们搭一个简单的中值滤波器。
一些基本原理:
S函数里面有一个switch case结构,还有一个flag标志,S函数会自动在每一个迭代过程中变换flag实现S函数中不同的功能,包括初始化、连续状态更新、离散状态更新、输出更新等等,这些都是MATLAB自动做的,这一点很像GUI的函数。sys是一个返回变量,根据flag的不同而又不同的功能,比如flag=3时sys就代表输出,如果不输出就写sys=[]。
一些注意点:
如果输出用到了输入u,一定记住初始化时sizes.DirFeedthrough = 1;
多输出或者多状态变量时各自都是列向量。
如果要用全局变量声明的时候global,在某一个函数里面使用的时候也要global一下。
x0多变量下一定要初始化。
ts第一个元素代表采样周期,第二个元素代表开始时间,离散的时候才需要考虑,连续的时候设置为0即可。
下面给出代码:
function [sys,x0,str,ts,simStateCompliance] = mymedfilt(t,x,u,flag)
% FLAG RESULT DESCRIPTION
% ----- ------ --------------------------------------------
% 0 [SIZES,X0,STR,TS] Initialization, return system sizes in SYS,
% initial state in X0, state ordering strings
% in STR, and sample times in TS.
% 1 DX Return continuous state derivatives in SYS.
% 2 DS Update discrete states SYS = X(n+1)
% 3 Y Return outputs in SYS.
% 4 TNEXT Return next time hit for variable step sample
% time in SYS.
% 5 Reserved for future (root finding).
% 9 [] Termination, perform any cleanup SYS=[].
switch flag
%%%%%%%%%%%%%%%%%%
% Initialization %
%%%%%%%%%%%%%%%%%%
case 0
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
%%%%%%%%%%%%%%%
% Derivatives %
%%%%%%%%%%%%%%%
case 1
sys=mdlDerivatives(t,x,u);
%%%%%%%%%%
% Update %
%%%%%%%%%%
case 2
sys=mdlUpdate(t,x,u);
%%%%%%%%%%%
% Outputs %
%%%%%%%%%%%
case 3
sys=mdlOutputs(t,x,u);
%%%%%%%%%%%%%%%%%%%%%%%
% GetTimeOfNextVarHit %
%%%%%%%%%%%%%%%%%%%%%%%
case 4
sys=mdlGetTimeOfNextVarHit(t,x,u);
%%%%%%%%%%%%%
% Terminate %
%%%%%%%%%%%%%
case 9
sys=mdlTerminate(t,x,u);
%%%%%%%%%%%%%%%%%%%%
% Unexpected flags %
%%%%%%%%%%%%%%%%%%%%
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 20;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1; %输出如果用到了u这里一定写1!虽然我这里输出没用到输入但是建议还是写1.
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
%
% initialize the initial conditions
%
x0 = zeros(20,1);
%
% str is always an empty matrix
%
str = [];
%
% initialize the array of sample times
%
ts = [0.1 0];
% Specify the block simStateCompliance. The allowed values are:
% 'UnknownSimState', < The default setting; warn and assume DefaultSimState
% 'DefaultSimState', < Same sim state as a built-in block
% 'HasNoSimState', < No sim state
% 'DisallowSimState' < Error out when saving or restoring the model sim state
simStateCompliance = 'UnknownSimState';
% end mdlInitializeSizes
%
%=============================================================================
% mdlDerivatives
% Return the derivatives for the continuous states.
%=============================================================================
%
function sys=mdlDerivatives(t,x,u)
sys = [];
% end mdlDerivatives
%
%=============================================================================
% mdlUpdate
% Handle discrete state updates, sample time hits, and major time step
% requirements.
%=============================================================================
%
function sys=mdlUpdate(t,x,u)
sys = med(x,u);
function p = med(x,u)
x = [0;x(1:19)];
x(1)=u;
p=x;
% end mdlUpdate
%
%=============================================================================
% mdlOutputs
% Return the block outputs.
%=============================================================================
%
function sys=mdlOutputs(t,x,u) %这个flag编写输出
sys = medfilt_calculate(x,u);
function y = medfilt_calculate(x,u)
a = medfilt1(x,10);
y = a(10);
% end mdlOutputs
%
%=============================================================================
% mdlGetTimeOfNextVarHit
% Return the time of the next hit for this block. Note that the result is
% absolute time. Note that this function is only used when you specify a
% variable discrete-time sample time [-2 0] in the sample time array in
% mdlInitializeSizes.
%=============================================================================
%
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sys = [];
% end mdlGetTimeOfNextVarHit
%
%=============================================================================
% mdlTerminate
% Perform any end of simulation tasks.
%=============================================================================
%
function sys=mdlTerminate(t,x,u)
sys = [];
% end mdlTerminate
保存为.m文件后在simulink下嵌入sfunction模块:
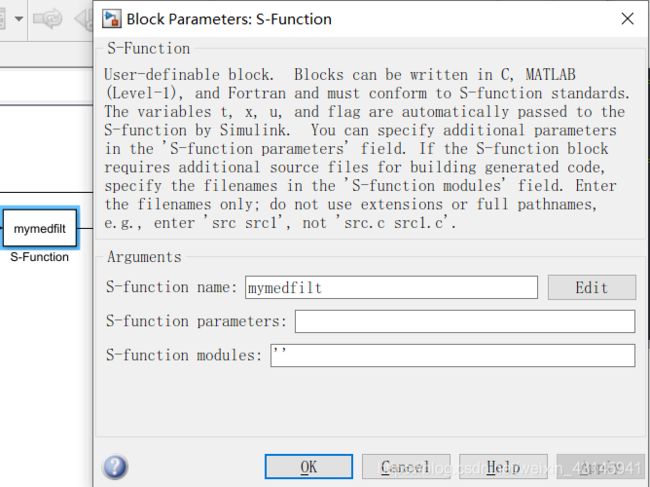
验证滤波效果:
搭建有噪声的正弦信号以及滤波模型:
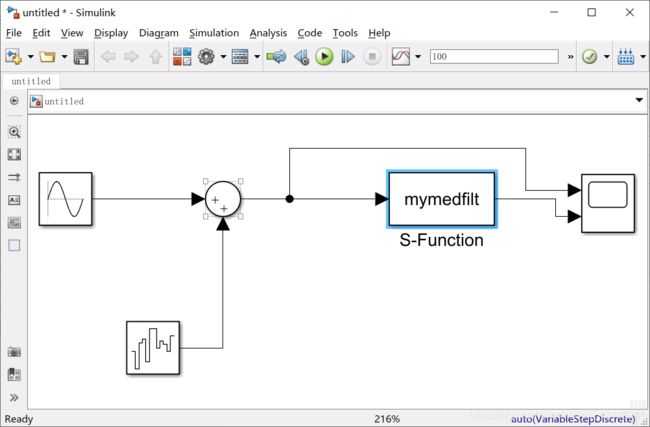
滤波效果肉眼可见,模块搭建成功。
Fcn模块的使用(时变系统仿真)
Fcn模块输入为一个向量,输出为一个数,这个数可以是这个向量各个元素的函数。下面以一个时变系统仿真举例:
y ′ ′ ( t ) + e − 0.2 t y ′ ( t ) + e − 5 t s i n ( 2 t + 6 ) y ( t ) = u ( t ) y''(t)+e^{-0.2t}y'(t)+e^{-5t}sin(2t+6)y(t)=u(t) y′′(t)+e−0.2ty′(t)+e−5tsin(2t+6)y(t)=u(t)
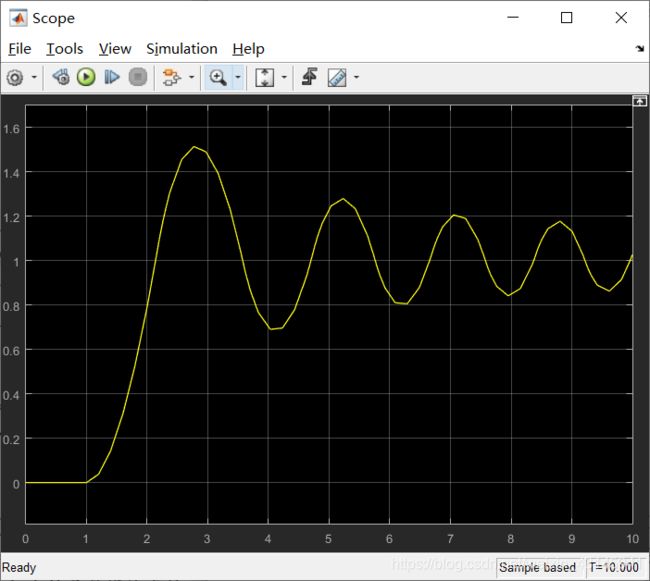
系统框图如下,仿真其阶跃响应。
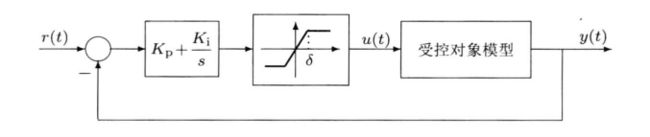
我们把这个微分方程形式转化为状态方程形式,令 x 1 ( t ) = y ( t ) , x 2 ( t ) = y ′ ( t ) x_1(t)=y(t),x_2(t)=y'(t) x1(t)=y(t),x2(t)=y′(t)。
x ′ ( t ) = x 2 ( t ) x 2 ′ ( t ) = − e − 0.2 t x 2 ( t ) − e − 5 t s i n ( 2 t + 6 ) x 1 ( t ) + u ( t ) x'(t)=x_2(t)\\x_2'(t)=-e^{-0.2t}x_2(t)-e^{-5t}sin(2t+6)x_1(t)+u(t) x′(t)=x2(t)x2′(t)=−e−0.2tx2(t)−e−5tsin(2t+6)x1(t)+u(t)
显然我们还是得使用两个积分器来作为构造基础,考虑到第二个式子等式右边除了u外有三个变量,我们把这三个变量通过Mux转换成一个向量,然后使用Fcn可以直接得出输出,下面是模型搭建:
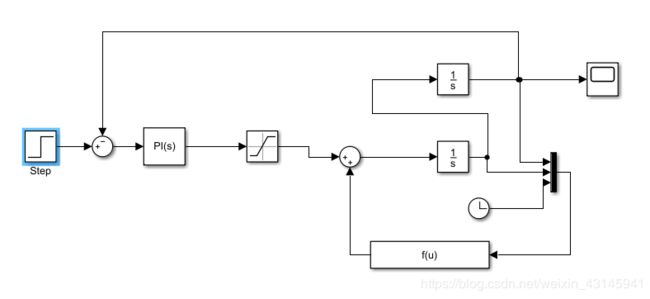
Fcn的设置:
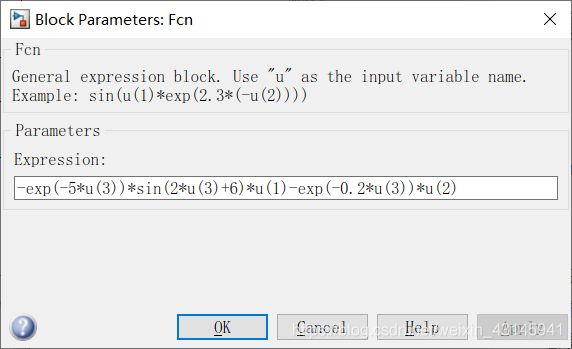
结果展示:
s函数编写:
function [sys,x0,str,ts,simStateCompliance] = time_varying(t,x,u,flag)
switch flag,
%%%%%%%%%%%%%%%%%%
% Initialization %
%%%%%%%%%%%%%%%%%%
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
%%%%%%%%%%%%%%%
% Derivatives %
%%%%%%%%%%%%%%%
case 1,
sys=mdlDerivatives(t,x,u);
%%%%%%%%%%
% Update %
%%%%%%%%%%
case 2,
sys=mdlUpdate(t,x,u);
%%%%%%%%%%%
% Outputs %
%%%%%%%%%%%
case 3,
sys=mdlOutputs(t,x,u);
%%%%%%%%%%%%%%%%%%%%%%%
% GetTimeOfNextVarHit %
%%%%%%%%%%%%%%%%%%%%%%%
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
%%%%%%%%%%%%%
% Terminate %
%%%%%%%%%%%%%
case 9,
sys=mdlTerminate(t,x,u);
%%%%%%%%%%%%%%%%%%%%
% Unexpected flags %
%%%%%%%%%%%%%%%%%%%%
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
%
% initialize the initial conditions
%
x0 = zeros(2,1);
%
% str is always an empty matrix
%
str = [];
%
% initialize the array of sample times
%
ts = [0 0]; %连续系统
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = [x(2);-exp(-0.2*t)*x(2)-exp(-5*t)*sin(2*t+6)*x(1)+u];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u)
sys = x(1);
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sys = [];
function sys=mdlTerminate(t,x,u)
sys = [];
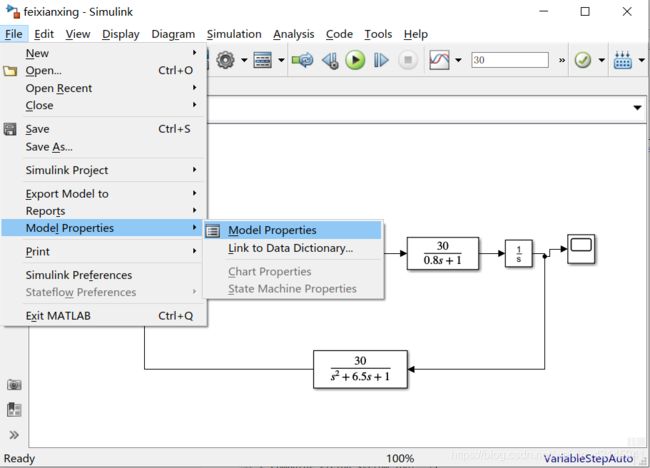
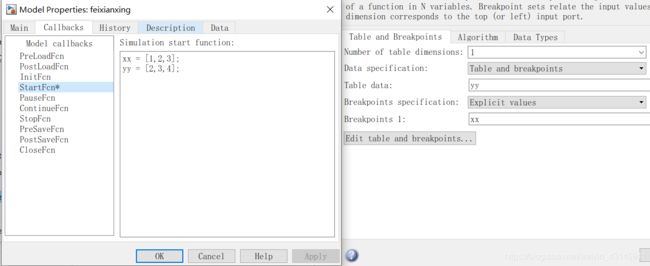
Simulink模型预置参数
很多情况下我们搭建的模型输入变量为参数,但由于每次重启MATLAB工作空间都会清除,因此带来了许多不方便。如果我们将一些初始化代码写在下面的地方,则可以在每次打开或者每次启动仿真时初始化模型。
Smith预估模型
Smith预估应用在被控对象有纯滞后的情况,传统的PID控制在直接控制的时候很容易发散,而Smith预估的思想就是构建一个相同模型利用模型未滞后的输出作为反馈,从而做到“及时纠正与控制”。下面用Simulink仿真数字Smith预估控制器,并且对比不用预估器模型的输出。
未进行预估:
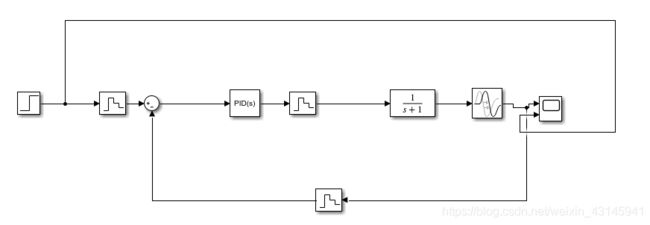
Smith预估:

从下往上数第二个反馈回路(示波器那根不算)就是Smith预估器。
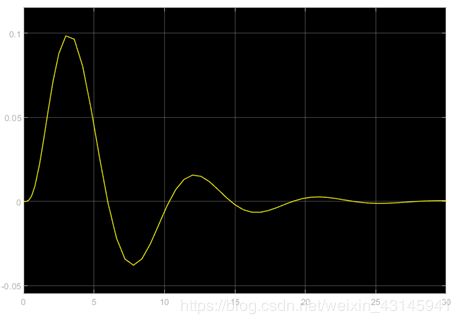
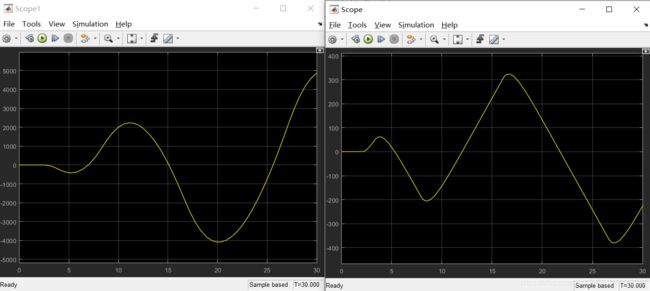
示波器显示结果对比:
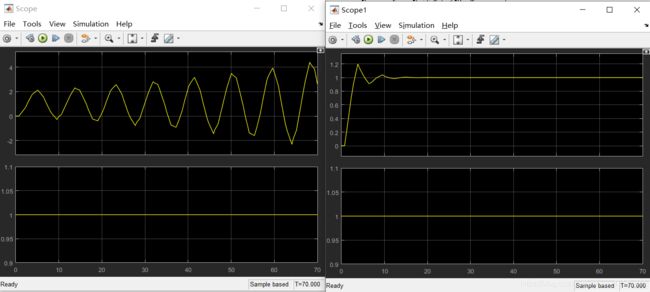
左边是不加预估器,明显看出系统发散,说明纯滞后对于系统危害很大。右边是使用Smith预估,系统收敛到给定值1。