CNN学习(一)
参考:> CS231n Convolutional Neural Networks for Visual Recognition
**
一、卷积神经网络(CNN/ ConvNet)
概述
- 由神经元组成,这些神经元具有可以被训练的权重和偏置。
- 输入图像像素,经过中间的函数,可以得到每个类别的分数。
- 一般的神经网络都是要输入一个向量,由于CNN输入的是图像,所以不用向量化,可以直接输入像素。
- 每个神经元连接上一层的一部分神经元,而不像全连接层那样连接上一层所有神经元。
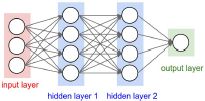
左边:常规的神经网络。
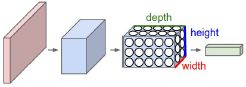
右边:输入的CNN的神经元是三维排列的(宽度、高度、深度(depth)),对于输入层(红色)来说,深度就是通道的层数,全彩图depth(R、G、B)就是3,灰度图就是1。输出也是个三维向量,图上的就是其中一层的切片。输出层是一个沿着深度维度排列的单个分数矢量,比如10类的输出,depth就是10,输出1x1x10的矢量。
和普通神经网络一样,都是卷积层、池化层、全连接层三层。
如CIFAR-10数据集。(CIFAR-10 是一个包含60000张图片的数据集。其中每张照片为32*32的彩色照片,每个像素点包括RGB三个数值,数值范围 0 ~ 255,所有照片分属10个不同的类别。)
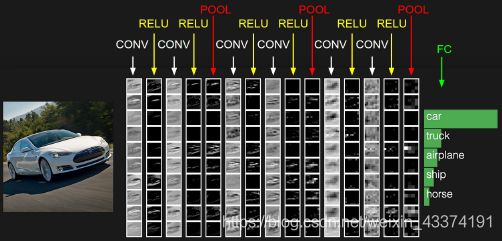
CIFAR-10数据集下,CNN具有架构[INPUT - CONV - RELU - POOL - FC]
- INPUT (输入层)将保持图像的原始像素值[32x32x3]。图像宽和高都是32,且具有三个颜色通道(RGB)。
- CONV(卷积层)计算每个连接到输入中的神经元的输出,每个神经元只连接上一层的一小块区域的神经元,每个神经元计算它们的权重与它们在输入体积中连接的小区域之间的点积。如果我们使用12个过滤器,就会产生深度为12的输出[32x32x12]。
- RELU(激活函数层)加入为非线性激活函数,保持体积的大小和深度保持不变([32x32x12])。
- POOL(池化层)将沿空间维度(宽度,高度)执行下采样操作,从而产生如[16x16x12]的输出。
- FC(全连接层)产生[1x1x10]的输出,例如10个类别的CIFAR-10,将输出每个类别的得分。顾名思义,该层中的每个神经元都将连接到前一层中的所有输出。
最终,CNN将输入的图像像素变成输出的类别分数。
某些层有参数,而某些层不包含参数。CONV/FC包括参数(权重和偏置),通过梯度下降进行训练。RELU/POOL是固定的。
综上所述 - ConvNet架构虽简单的情况是一些层,它将图像转换为输出(例如,分类的分数)
- 有几种不同类型的图层(例如CONV / FC /RELU / POOL是目前最流行的)
- 每个图层都接受输入三维数据,并通过可微分函数将其转换为输出三维数据
- 每个层可能有参数(CONV / FC 有,RELU / POOL没有)
- 每个层可能有额外的超参数(CONV /FC / POOL有,RELU没有)p.s.超参数是预先设置好值的参数,需要进行不断优化
二、各个层的超参数及连接性的细节
1.卷积层
Conv层是CNN的核心模块,完成大部分繁重的计算工作。
没有神经元类比的卷积层
卷积层参数由一系列可学习的过滤器组成,过滤器在空间上沿着宽度和高度方向非常小,但是延伸到输入体积的整个深度,例如,CNN在第一层上的典型过滤器可能具有5x5x3的大小(5像素宽度和高度,深度是3,因为图像深度就是3)。前向传递中,每个过滤器在输入的宽度和高度上滑动(卷积),并计算过滤器与输入图像对应位的点乘。当滤波器滑动的时候,每个过滤器都会生成一个二维的CAM(class activation map),表示输入中的什么区域能够指示CNN进行正确的识别,网络看到某种视觉特征时就会激活,例如某些方向的边缘或第一层上某种颜色的斑点,或最终在网络的更高层上的整个蜂窝或轮状图案。如果每个卷积层中有一整套过滤器(例如12个),并且每个过滤器都会生成一个二维CAM,最后输出就是沿深度堆叠这些CAM图。
类比神经元
每个输出都可以理解为在空间上看到了输入中的一个小区域并且与所有神经元共享参数(因为这些数字都用了相同的滤波器)。我们现在讨论神经元连通性的细节,它们在空间中的排列以及它们的参数共享方案。
局部连接
当处理高维输入(如图像)时,将神经元连接到上一层中的所有神经元是不切实际的。相反,我们将每个神经元连接到输入的局部区域。这种连接的空间范围是一个超参数,称为神经元的感受野(相当于过滤器大小)。连接在空间(沿宽度和高度)中是局部的,但是深度是完整的(深度上的连接范围永远等于输入的深度)。
例1,假设输入(如RGB CIFAR-10图像)大小为[32x32x3],如果感受野(过滤器大小)是5x5,那么卷积层中的每个神经元将具有输入中[5x5x3]区域的权重,总共5 * 5 * 3 = 75个权重参数(和+1的偏置参数),沿深度方向的范围必须是3,因为输入的深度就是3.
例2,假设输入大小为[16x16x20]。然后使用3x3的示感受野,卷积层中的每个神经元具有3 * 3 * 20 = 180个连接。同样,连接在空间中是局部的(3x3),但在深度(20)上是完整的。
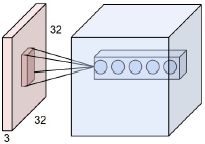
红色的表示输入(例如32x32x3的CIFAR-10图像),蓝色的卷积层每个神经元空间上连接一个区域,深度上是3,图中的卷积层深度上有5个神经元。
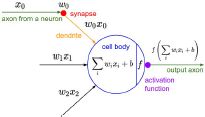
前向传播时,神经元还是计算输入与权重的点积和偏置以及加入激活函数(非线性),只是输入的连接被限制在局部。
空间排列
下面讨论输出神经元的个数以及他们的空间排布。三个超参数控制输出的大小:深度(depth)、步长(stride)、和补0(zero-padding)。
- 深度:对应使用过滤器的数量。每次学习都是在输入中寻找不同的特征,
例如第一个卷积层的输入是原始图像,不同的神经元激活不同的方面,比如各种特定方向边缘、颜色斑点等。连接同一块区域的一组神经元叫做depth column - 步长:步长为1时,过滤器移动一个像素,步长为2时,移动2个像素,输出会变少。
- 补0:可以控制输出的空间大小(通常用于控制输出的大小和输入相同)。
定义符号:
W:输入空间大小
F:感受野大小
S:步长
P:边框使用的0填充量
输出大小(空间上神经元个数):(W - F + 2 P )/ S + 1
7x7的输入中,假定P=0,用3x3的过滤器,步长为1时,输出为5x5,步长为2时,输出为3x3,输出大小不为整数时,说明P和S选的不合适
参数共享
每个深度的权重和偏差被这个深度上的所有神经元共享。反向传播中,我们仍然可以使用梯度下降的方法来学习这些权重,只需要对原始算法做一些小的改动, 这里共享权值的梯度是所有共享参数的梯度的总和。
有时候 需要在空间上的不同区域采用不同的检测方法,提取不同特征时,就会放松参数共享方案。
Numpy Examples
输入:数组X
在点(x,y)的depth column:X[x,y,:]
深度为d的depth slice: X[:,:,d]
假设:输入的X为X.shape: (11,11,4),不使用0填充(P=0),过滤器大小为5(F=5),步长为2(S=2),输出的大小为(11-5+0)/2+1=4,输出的宽和高都为4,输出的activation map(V)
V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0
//在这里W0其实是W0.shape(5,5,4)
V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (沿着y方向)
V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (x y两个方向)
这些activation map后往往会跟着激活函数(非线性)
总结:
-
接收的输入:
W1 × H1 × D1 -
卷积层有4个超参数 :S(步长),F(过滤器大小/感受野),K(过滤器个数),P(补0)
-
输出大小:
W2 × H2 × D2W2 = (W1 − F + 2P)/S + 1 H2 = (H1 − F + 2P)/S + 1 D2=K
通过权值共享,每个过滤器都会产生F*F*D1个权值,一共F*F*D1*K个权值和K个偏置
-
在输出单元,第d个深度切片的结果是由第d个过滤器和输入单元做卷积运算,然后再加上偏置而来。
反向传播:反向传播的数据和权重的卷积是通过具有空间翻转的过滤器
1x1的卷积:在二维输入上没有意义,但是在多维上1x1的卷积是延伸到整个深度的
扩张的卷积:过滤器中间有空格
扩张参数为0的卷积:w[0]*x[0] + w[1]*x[1] + w[2]*x[2]
扩张参数为1的卷积:w[0]*x[0] + w[1]*x[2] + w[2]*x[4]
2.池化层
作用:逐步减小表示的空间大小,以减少网络中的参数和计算量,从而也控制过度拟合。
最常用的池化层是2x2的过滤器,输出这四个值中最大的那一个
两个常见的最大池化层:F = 3 ,S = 2和F = 2 ,S = 2
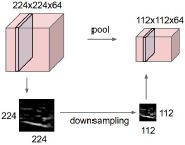
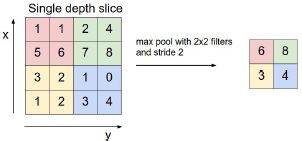
左边采用2x2步长为2的过滤器,深度保持不变
去掉池化层在训练良好的生成模型中很重要,例如变分自动编码器(VAE)或生成性对抗网络(GAN)。未来的架构很可能只有很少甚至没有池化层。
3.全连接层
全连接层和卷积层的唯一区别就是卷积层是连接局部的输入,并且共享权值和偏置参数,但是,全连接层也是计算矩阵的点积,所以他们的函数形式是一致的。所以全连接层和卷积层是可以相互转换的。
卷积层转化到全连接层:过滤器变成一个很大的矩阵,除了某些必要的块之外其他的都是0(局部连接),并且很多块是相等的(权值共享)。
全连接层转化到卷积层:一个K = 4096的全连接层,输入是7 × 7 × 512的,就相当于F = 7, P = 0, S = 1, K = 4096的卷积层,也就是过滤波器的大小和输入的大小相同。输出是1 × 1 × 4096的。
这两类转换中,全连接层到卷积层的转换是很有意义的。
有一个224x224x3的图像作为输入的卷积神经网络,经过一系列的卷积池化,变成大小为7x7x512,然后使用两个大小为4096的全连接层,最后使用1000个神经元来计算类别得分。我们可以将这三个全连接层转化为卷积层。 -
第一个全连接层:使用
F=7的过滤器,将7 × 7 × 512大小的输入变成1x1x4096的输出 -
第二个全连接层:使用
F=1的过滤器,输出仍然是1x1x4096 -
第三个全连接层:使用
F=1的过滤器,输出是1x1x1000
每次转换实际上是把全连接层的权重矩阵W转换为 卷积层的过滤器,如果图像变大了,全连接层就不需要重写,而是滑动过滤器,就可以得到类别分数。
例如:224x224的图像通过卷积层和池化层变成7 × 7 × 512(7=224/32),这时输入一个384x384的图像,通过卷积层和池化层将会变成12 × 12 × 512(384/32),通过最后三层全连接层时会变成6x6x1000,(12-7)/1+1=6,这时每一类的类别分数不是一个数而是一个6x6的矩阵。
由于这6x6=36个位置都使用相同的计算方法,所以转换后的全连接层比原始的迭代36次高效的多。通常用于增大图片大小时,可以得到很多空间位置的类别得分,然后将这些得分求平均数。
4.CNN架构
卷积网络通常只由三种类型的层组成:CONV(卷积层),POOL(池化层,假设Max池化)和FC(全连接层)。我们还将RELU激活函数明确地写为一个层,在这里加入了非线性元素。
最常见的CNN架构如下:
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC (*表示重复几次,POOL?表示池化层是可选的,并且M,N,K都是>=0的,通常N<=3,K<3)
堆叠一些CONV-RELU层,紧跟着一个POOL层,并重复此模式,直到图像在空间上合并为小尺寸。在某些时候,过渡到全连接层是很常见的。最后一个全连接层保存输出,例如类别得分。