机器学习09-异常检测
文章目录
- 异常检测算法
- 步骤
- 例子
- 开发和评估异常检测系统
- 异常检测 VS 监督学习
- 异常检测
- 监督学习
- 选择要使用的功能
- 使数据接近高斯分布
- 如何得到异常检测算法的特征
- 多变量高斯分布
- μ , ∑ \mu,\sum μ,∑ 对 p ( x ) p(x) p(x) 的影响
- 使用多变量高斯分布的异常检测
- 步骤
- 多变量高斯分布异常检测算法与原始算法的区别
- 造成 ∑ \sum ∑不可逆的原因
异常检测算法
步骤
- 选取能够描述所收集数据一般特性的特征 x i x_i xi(当数据异常时,这些特征会特别大或特别小)
- 计算参数 μ 1 , μ 2 , . . . , μ n , σ 1 2 , σ 2 2 , . . . , σ n 2 \mu_1,\mu_2,...,\mu_n,\sigma_1^2,\sigma_2^2,...,\sigma_n^2 μ1,μ2,...,μn,σ12,σ22,...,σn2(假设有 n 个特征)
μ j = 1 m ∑ i = 1 m μ j ( i ) , σ j 2 = 1 m ∑ i = 1 m ( x j ( i ) − μ j ) 2 \mu_j = \frac{1}{m}\sum_{i=1}^m\mu_j^{(i)},\sigma_j^2 = \frac{1}{m}\sum_{i=1}^m(x^{(i)}_j - \mu_j)^2 μj=m1i=1∑mμj(i),σj2=m1i=1∑m(xj(i)−μj)2
μ = [ μ 1 μ 2 ⋮ μ n ] = 1 m ∑ i = 1 m μ ( i ) \mu = \begin{bmatrix} \mu_1\\ \mu_2\\ \vdots\\ \mu_n \end{bmatrix} = \frac{1}{m}\sum_{i=1}^m\mu^{(i)} μ=⎣⎢⎢⎢⎡μ1μ2⋮μn⎦⎥⎥⎥⎤=m1i=1∑mμ(i) - 给定新的样本 x,计算 p(x)
p ( x ) = ∏ j = 1 n p ( x j ; μ j , σ j 2 ) = ∏ j = 1 n 1 2 π σ j e x p ( − ( x j − μ j ) 2 2 σ j 2 ) p(x) = \prod_{j=1}^n p(x_j;\mu_j,\sigma^2_j) = \prod_{j=1}^n \frac{1}{\sqrt {2\pi}\sigma_j}exp(-\frac{(x_j - \mu_j)^2}{2\sigma_j^2}) p(x)=j=1∏np(xj;μj,σj2)=j=1∏n2πσj1exp(−2σj2(xj−μj)2)
如果计算出 p ( x ) < ϵ p(x) < \epsilon p(x)<ϵ,则将该项标注为异常
例子
假设有一个数据集,其特征 x 1 , x 2 x_1,x_2 x1,x2 的正太分布如下图:
将所有特征的概率相乘,则得到 p ( x ) p(x) p(x) 如下图
设定阈值 ϵ = 0.02 \epsilon = 0.02 ϵ=0.02,当有一个新样本 x t e s t ( 1 ) x_{test}^{(1)} xtest(1) 位于上上图粉红色区域内时,假设 p ( x t e s t ( 1 ) ) = 0.0426 ≥ ϵ p(x_{test}^{(1)}) = 0.0426 \geq \epsilon p(xtest(1))=0.0426≥ϵ,则将该样本标注为正常。
当有一个新样本 x t e s t ( 2 ) x_{test}^{(2)} xtest(2) 位于上上图粉红色区域外时,假设 p ( x t e s t ( 2 ) ) = 0.0021 < ϵ p(x_{test}^{(2)}) = 0.0021 < \epsilon p(xtest(2))=0.0021<ϵ,则将该样本标注为异常。
而这个阈值 ϵ \epsilon ϵ 就相当于给上上图划定了一个边界,位于边界内标为正常,边界外标为异常。对应上图的 p(x),当 p ( x ) ≥ ϵ p(x) \geq \epsilon p(x)≥ϵ,正常;当 p ( x ) < ϵ p(x) < \epsilon p(x)<ϵ,异常。
开发和评估异常检测系统
对于一个新的特征,我们很难选择要不要将其纳入数据集中,如果有一个算法能够返回一个实数,比较加入这个特征和不加入特征的情况,便很容易选择要不要这个特征。异常检测系统能够很好的实现这一点。
假设我们有一些带标签的样本, y = 0 表示正常,y = 1 表示异常,将其分为训练集、验证集和测试集。
- 训练集:假设全是正常样本,没有异常样本(就算不小心参入 了异常样本也没关系)
- 验证集:既有正常样本也有异常样本
- 测试集:既有正常样本也有异常样本
举个例子:
假设有10000个正常样本(y = 0,即使里面不小心参入了异常样本,也将其视为正常),20个异常样本(y = 1),将他们分为:
- 无标签训练集(尽管我们知道标签 y=0):6000个,通过这6000个正常样本计算出 p(x),拟合出参数 μ , σ 2 \mu,\sigma^2 μ,σ2
- 验证集:2000个正常样本(y = 0),10个异常样本(y = 1)
- 测试集:2000个正常样本(y = 0),10个异常样本(y = 1)
步骤:
- 在训练集中计算出 p ( x ) p(x) p(x)
- 预测验证集或测试集样本x, y = { 1 i f p ( x ) < ϵ ( 异 常 ) 0 i f p ( x ) ≥ ϵ ( 正 常 ) y = \begin{cases} 1~~~~~~ if~~ p(x) < \epsilon~~(异常)\\ 0~~~~~~if ~~p(x) \geq \epsilon~~(正常) \end{cases} y={1 if p(x)<ϵ (异常)0 if p(x)≥ϵ (正常)
- 评估算法性能
- 真阳性、假阳性、真阴性、假阴性
- 精确率/召回率
- F1-score
此外,还可以在验证集中设置参数 ϵ \epsilon ϵ 的值。
一般来说,我们使用训练集,验证集和测试集的方法是:进行决策时(比如要不要选择某个特征或选择 ϵ \epsilon ϵ 的值),在交叉验证集中评估算法,选择好要使用的特征和 ϵ \epsilon ϵ 后,在测试集中进行最后的评估。
异常检测 VS 监督学习
异常检测
- 正样本很少(y = 1)(0-20是常见的)
- 负样本(y = 0)很多
- 很多种不同类型的异常
- 未来出现的异常可能跟见到的异常完全不同
监督学习
- 有大量的正样本和负样本
- 新加入的样本跟训练集中的样本相似
选择要使用的功能
使数据接近高斯分布
在进行异常检测算法时,我们使用高斯分布来对数据建模。即使数据不是呈高斯分布,算法也能正常运行。但是对其进行转换使其更接近高斯分布,或许能使算法更好的运行。
常见的数据转换方法有:
- x 1 ← l o g ( x 1 ) x_1 \leftarrow log(x_1) x1←log(x1)
- x 2 ← l o g ( x 2 + c ) x_2 \leftarrow log(x_2 + c) x2←log(x2+c)
- x 3 ← x 2 1 n x_3 \leftarrow x_2 ^{\frac{1}{n}} x3←x2n1
如何得到异常检测算法的特征
误差分析法:先训练出一个完整的算法,在一组交叉验证集上找出预测出错的样本,看看能不能找到其他一些特征来帮助学习算法,让那些在交叉验证上出错的样本学习的更好。
当 x 为正常样本时,p(x) 很大,而当 x 为异常样本时,p(x)很小
但是当把一个异常样本预测为正常样本时,p(x) 都很大
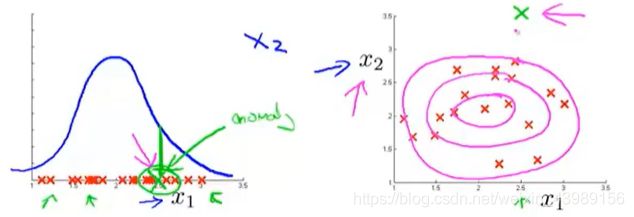
如下图,对一个异常样本(绿色),如果我们用特征 x 1 x_1 x1 来计算 p(x),则会把该样本预测为正常样本。这时可以尝试找出新的特征 x 2 x_2 x2 使异常样本与正常样本区别开来。
多变量高斯分布
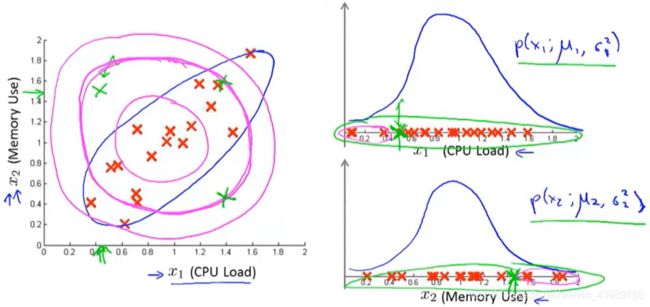
单变量高斯分布无法将特征结合,如下图,对于异常样本(绿色),若使用单变量高斯分布,则很容易将其判断为正常样本,因为 p ( x 1 ) , p ( x 2 ) p(x_1),p(x_2) p(x1),p(x2)都挺大的。
为了解决这个问题,提出多元高斯分布。
对于 x ∈ R n x \in \Bbb R^n x∈Rn,不分别建立 p ( x 1 ) , p ( x 2 ) , . . . p(x_1),p(x_2),... p(x1),p(x2),...模型,而是为所有 p ( x ) p(x) p(x) 建立统一模型。
多元高斯分布的参数是 μ ∈ R n \mu \in \Bbb R^n μ∈Rn,协方差矩阵 ∑ ∈ R n × n \sum \in \Bbb R^{n \times n} ∑∈Rn×n
p ( x ; μ , ∑ ) = 1 ( 2 π ) n 2 ∣ ∑ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T ∑ − 1 ( x − μ ) ) p(x;\mu,\sum) = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}exp(-\frac{1}{2}(x - \mu)^T\sum^{-1}(x-\mu)) p(x;μ,∑)=(2π)2n∣∑∣211exp(−21(x−μ)T∑−1(x−μ))
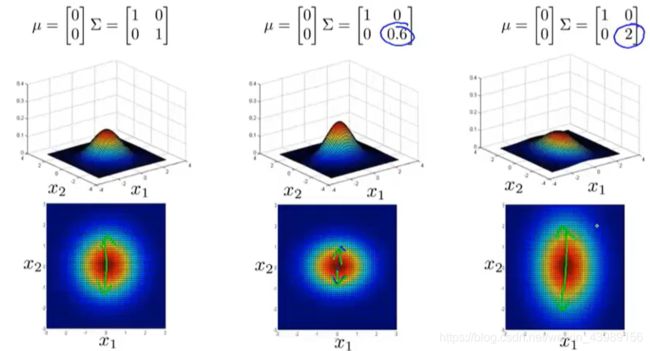
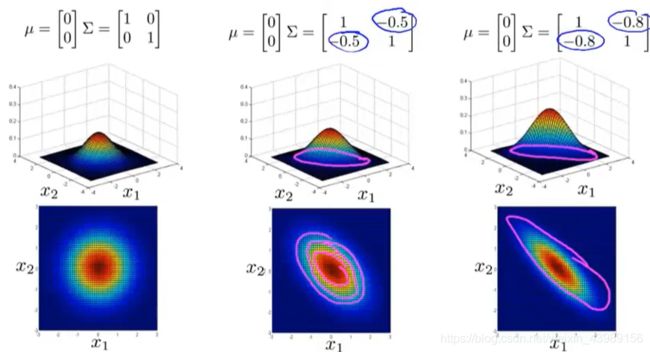
μ , ∑ \mu,\sum μ,∑ 对 p ( x ) p(x) p(x) 的影响
使用多变量高斯分布的异常检测
步骤
- 计算
μ = 1 m ∑ i = 1 m x ( i ) \mu = \frac{1}{m}\sum_{i=1}^mx^{(i)} μ=m1i=1∑mx(i)
∑ = 1 m ∑ i = 1 m ( x ( i ) − μ ) ( x ( i ) − μ ) T \sum = \frac{1}{m}\sum_{i=1}^m(x^{(i)} - \mu)(x^{(i)} - \mu)^T ∑=m1i=1∑m(x(i)−μ)(x(i)−μ)T - 给出一个新样本,计算
p ( x ) = 1 ( 2 π ) n 2 ∣ ∑ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T ∑ − 1 ( x − m u ) ) p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}|\sum|^{\frac{1}{2}}}exp(-\frac{1}{2}(x - \mu)^T\sum^{-1}(x-mu)) p(x)=(2π)2n∣∑∣211exp(−21(x−μ)T∑−1(x−mu)) - 比较 p(x) 与 ϵ \epsilon ϵ
多变量高斯分布异常检测算法与原始算法的区别
事实上,原始算法是多变量高斯算法当 ∑ = [ σ 1 2 0 0 ⋯ 0 σ 2 2 0 ⋯ ⋮ 0 0 ⋯ σ n 2 ] \sum = \begin{bmatrix} \sigma_1^2 ~~0~~0~~\cdots\\ 0~~\sigma_2^2~~0~~\cdots\\ \vdots\\ 0~~0~~\cdots~~\sigma_n^2 \end{bmatrix} ∑=⎣⎢⎢⎢⎡σ12 0 0 ⋯0 σ22 0 ⋯⋮0 0 ⋯ σn2⎦⎥⎥⎥⎤的一种特殊情况
原始算法:
- 手动添加新的特征来整合原始特征 x 1 , x 2 x_1,x_2 x1,x2
- 计算成本低,能适应 n 比较大的情况
- 当训练样本 m 比较小时也能运行
多变量高斯分布异常检测算法:
- 自动整合特征之间的关系
- 计算成本高
- 训练样本 m 必须大于特征 n,否则 ∑ \sum ∑ 不可逆
造成 ∑ \sum ∑不可逆的原因
- m ≤ n m \leq n m≤n
- 存在冗余特征,比如 x 3 = x 1 + x 2 x_3 = x_1 + x_2 x3=x1+x2,此时 x 3 x_3 x3就是一个冗余特征。