【论文笔记】Reaching agreement in the presence of faults (EIG)
文章目录
- 1 问题定义
- 2 交互一致性
- 3 单点故障
- m=1 n=4
- 4 多点故障(n>=3m+1)
- 计算过程
- m=2 n=7
- 5 n<3m+1不能达成协定
- 6 带认证的算法
- 7 总结
这篇论文在1980年发表,是1982年著名的 拜占庭将军问题论文的前身。作者Leslie Lamport是2013图灵奖得主,两篇论文引用次数分别为5000+和2000+。该论文提出的算法现在被称为EIG算法(EIG全称指数信息收集),因为消息的数量是和节点数量呈指数关系。
“Reaching Aggrement in the Presence of Faults ” M. PEASE, R, SHOSTAK, AND L. LAMPORT, 1980.
“The Byzantine General Problem” Leslie Lamport, Robert Shostak, and Marshall Pease ,1982
1 问题定义
一个分布式的处理系统具有多个处理节点,要保证可靠就必须具有容错性,能够在部分节点故障的情况下正常工作。而本算法解决的问题是与一些相互隔离的处理节点相关,其中有一些节点可能是故障的,节点之间只能通过双方之间的消息传递进行通信。
问题定义如下:
- n个独立节点组成的集合,故障节点数量不超过m
- 节点之间只能通过双方之间的信息进行通信 (不存在第三方监听捣乱以及信道故障的问题,也就是说消息一定能传递到对方,并且认为传递的时延是几乎一致,不存在时延问题,并且接收方总是可以识别消息的发送方)
- 每个非故障的节点有一个私有值 (private value),用来与其他节点进行通信
- 非故障节点总是“诚实地”进行通信,故障节点可能“说谎” (传递错误消息)
算法设计目标:
- 推断出的某非故障节点值必须是该节点的私有值
- 每个非故障节点推断出的故障节点的值必须一致
目标本质上是使非故障节点达成共识
2 交互一致性
为了介绍算法该论文定义了一个叫做交互一致性的概念来阐述。交互一致性定义如下:
考虑由n个独立节点组成的集合,已知故障节点数量不超过m。假设节点之间通信只能有双方参与,传输时延可以忽略不计。接收方总是可以识别消息的发送方。假设节点p有某个私有值Vp (例如它的时钟值或者读某个传感器的值)。问题可以归结如下:对于给定的大于零的值m,n,是否可能设计一个基于消息传递的算法使每个非故障节点p计算一个值向量,其中每个元素对应每个节点。其中:
- 每个非故障节点计算出完全一致的向量
- 向量中对于指定某个非故障节点的元素值是该节点的私有值
注意:该算法并不需要确定出哪些节点是故障的,重点在于使所有非故障节点计算出的向量的值是相同的。
算法对于 n > = 3 m + 1 n>=3m+1 n>=3m+1可解,其中n为节点总数,m为故障节点数
计算出的向量称为一致性向量(interactive consistency vector,ICV)
因为每个非故障节点可以根据应用需要对向量使用平均或者滤波函数,对同一个向量使用相同的函数,所以共识一定能够达成。
3 单点故障
首先我们从满足该条件的最简单的例子m=1,n=4开始介绍。
整个处理流程包含两部分,消息的交换以及基于交换结果的交互一致性向量的计算。单点故障需要两轮信息交换。第一轮节点交换它们的私有值,第二轮它们交换第一轮得到的结果。
在整个过程中故障节点可能“说谎”,即传递错误的信息,或拒绝发送信息。
消息的交换
- Round1:节点交换各自私有值
- Round2:交换第一轮得到的值
ICV向量计算
- 投票
当消息交换完成后,每个非故障节点p在各自向量上对应p的位置记录自己的私有值Vp。而对应于另外三个节点q的元素,根据检验接收的三个q的值来确定。其中一个通过第一轮从q获得,其他两个通过第二轮从剩余两个节点获得。如果三个值中至少两个相同,则该数值被采用,否则采用一个默认值“NIL”。
m=1 n=4
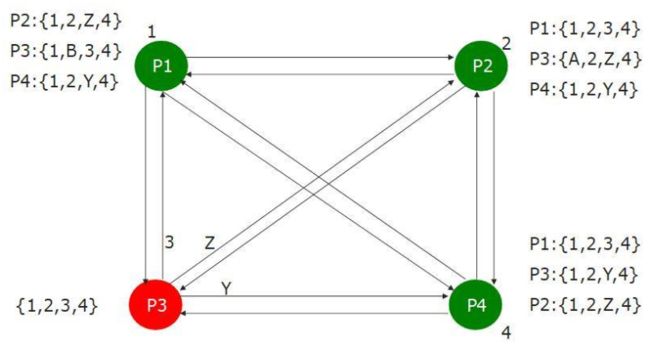
下面用图来详细说明整个过程:假设P1、P2、P4为非故障节点,而P3为故障节点。P1,P2,P3,P4的私有值分别为{1,2,3,4,}。P3在第一轮传递给P1、P2、P4的私有值分别为3、Z、Y。以P1收到的消息为例,P1收到来自P2的消息向量为{1,2,Z,4},即P2在第一轮传递的P2私有值为2,在第二轮转发第一轮收到的P3私有值Z及P4私有值4。同理P1收到P3的消息向量为{1,B,3,4},收到P4的消息向量为{1,2,Y,4}。两轮消息传递后,统计P2,P3,P4的消息向量同一单元位置出现次数大于2次的值,设为ICV元素值,如果没有则设置为NIL。得到P1的ICV为{1,2,NIL,4}。
按照以上方法分析,同理可以得到剩余两个非故障节点P2和P4的ICV为{1,2,NIL,4},因此所有非故障节点的ICV相同,达成共识。如果{3,Z,Y}中有两个元素以上相等,该非NIL值设为v,则可以分析得到最后P1,P2,P4的ICV也必相等,为{1,2,v,4}。
4 多点故障(n>=3m+1)
- 对于单点故障 -> 需要2轮信息交换
- 对于m点故障 -> 需要m+1轮信息交换
其中第一轮是交换私有值,接下来的m轮交换上一轮收到的值。整个过程是指数级别的,所以也称为指数信息收集算法(EIG)。
设 P P P为节点集合 , V V V为值的集合
k≥1: k-level scenario -> mapping from a set of non-empty strings p 1 , p 2 , p 3 , … p n {p1,p2,p3,…pn} p1,p2,p3,…pn over P P P of length < = k + 1 <=k+1 <=k+1, to V V V
Example: For a k-level scenario σ and string w = p 1 p 2 … p n , σ ( ω ) w=p1p2…pn ,σ(ω) w=p1p2…pn,σ(ω)= the value of p n pn pn that p n pn pn tells p n − 1 p_{n-1} pn−1 … which p 2 p_2 p2 tells p 1 p_1 p1
对于一个给定的k水平场景σ和字符串 ω = p 1 p 2 p 3 ⋯ p n ω=p1p2p3⋯pn ω=p1p2p3⋯pn, 2 < = n < = k + 1 2<=n<=k+1 2<=n<=k+1, σ ( ω ) σ(ω) σ(ω)用来表示pn的私有值经过 p n − 1 p n − 2 ) ⋯ p 2 p_{n-1} p_{n-2})⋯p2 pn−1pn−2)⋯p2的传递最后到达传递给 p 1 p1 p1的值。
对于单元素的字符串 σ ( p σ(p σ(p)表明 p p p的私有值。一个k水平的场景总结了经过k轮的信息交换的结果。对于每个非故障节点q,任意节点p以及字符串 w w w,有 σ ( p q ω ) = σ ( q ω ) σ(pqω)=σ(qω) σ(pqω)=σ(qω)成立。
计算过程
节点p接收的信息以p开始的字符串限定,记为 σ p σ_p σp。对于任意m>=0,n>=3m+1,给定 σ p σ_p σp下对某个节点q的计算过程如下:
- 如果P的某个大小≥(n+m)/2的子集Q,如果对于每个长度不大于m的字符串w(Q中元素组成),有 σ p σ_p σp (pωq)=v,则p记录v
- 如果没有,则算法将m-1,n-1带入进行递归。此时P用P-{q}代替, σ p ( p ω q ) σ_p (pωq) σp(pωq)用 σ p ( p ω ) σ_p (pω) σp(pω)代替。对于每个字符串长度不大于m的字符串w,如果在这向量n-1个元素里有至少(n+m)/2个元素值相同,p记录下该值,否则记录NIL值。
m=2 n=7
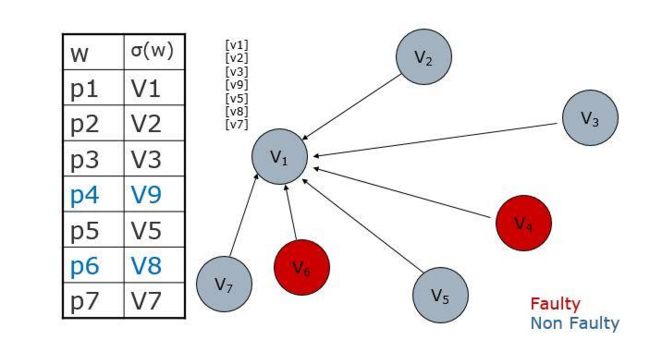
下面以m=2,n=7为例介绍多点故障下的算法流程。如图所示一共有7个节点,其中节点4和节点6是故障节点,其余为非故障节点。第一轮信息交换,节点之间互相传递各自的私有值,可以看到节点4和节点6伪造各自的私有值进行传递。
以节点1为例,列出所有满足的 σ p ( p ω q ) σ_p (pωq) σp(pωq)的情况进行判断,最后可以得到节点1的向量为{V1,V2,V3,NIL,V5,NIL,V7}。最后所谓非故障节点将得到的向量也是{V1,V2,V3,NIL,V5,NIL,V7},满足交互一致性,达成协定。
5 n<3m+1不能达成协定
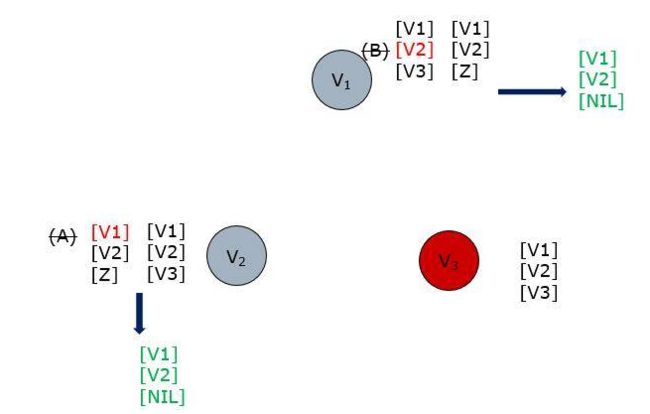
下面以m=1,n=3为例说明 n < 3 m + 1 n<3m+1 n<3m+1时不能达成共识。如图所示,节点3是故障节点,节点1和节点2是非故障节点;我们可以看到节点1和节点2的向量中元素没有一个大多数值,例如节点1向量关于第2个元素值有一个B和一个V2,没有一个数占大多数,也就无法达成共识。
6 带认证的算法
n<3m+1情况下无法达成协定是基于故障节点可能拒绝传递或者伪造从其他节点那收到的值。
而使用认证可以保证故障节点虽然可能在传递自己私有值时撒谎或者拒绝发送自己的私有值,但是不能错误转发从其他节点收到的值。
使用认证的方法是在消息中加入签名,该签名只能由发送方创建。接收方可以使用验证器来检验发送方以及值是否正确。公钥和私钥结合对消息进行Hash可以达到以上目的。
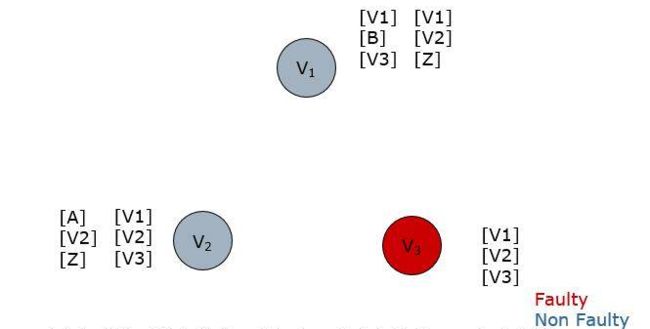
下面以m=1,n=3举例。在使用带有认证的算法时,节点3无法伪造收到的节点1和节点2的值,所以可以看到节点1中两个向量的第二个元素都是V2,节点2中两个向量的第一个元素都是V1。最终两个节点得到的向量均相同,并且非故障节点元素为节点的私有值,满足交互一致性的定义,也就达成了协定。
7 总结
- 这篇论文是拜占庭问题论文的前身,基本介绍了拜占庭问题的内容。
- 提出了交互一致性的概念用来描述协定问题,对于分布式容错系统的设计而言交互一致性是必要的。
- 并且提出了EIG算法用于解决拜占庭协定问题。
在该问题中,故障节点可以伪造自己的私有值以及收到的来自其他节点的数据。在故障节点数目少于总结点数的三分之一时,使用该算法可以有效地使非故障节点达成一致。当故障节点数大于等于总结点数三分之一时,节点无法达成协定。
此外,当使用带有认证的机制时,在该协定条件下故障节点可以伪造自己的私有值但无法伪造收到的来自其他节点的数据,在此限定下非故障节点可以达成协定。