计算流体力学简介(四)——有限差分法

基本原理

有限差分法的原理很简单，就是利用差商代替微分，利用泰勒展开得到微分项的差商近似，从而求出方程的近似解。
记差分算子$E^{k}f=f(x+kh)$，微分算子$D^{k}f=\frac{{\partial }^{k}f}{\partial x^k}$
利用差分算子和微分算子表示泰勒展开有
$Ef=If+hDf+\frac{1}{2}{h}^2{D}^{2}f+\cdots +\frac{1}{n!}{h}^n{D}^{n}f+\cdots$
所以得到
$E=I+Dh+\cdots +\frac{1}{n!}{h}^n{D}^n+\cdots =e^{hD}$
反过来
$D=\frac{1}{h}lnE=\frac{E-I}{h}+\cdots +\frac{(-1{)}^{n-1}(E-I{)}^n}{nh}+\cdots$
利用这个算子可以很容易的推到各阶的差商近似关系，同时可以利用这个关系来构造利用离散点导数信息的紧致格式。

一维对流方程

$\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}=0$
初场为$u_0(x)=e^{-x^2}，x\in [-5,5]$周期边界
$\Delta x$取为$\frac{10}{32}$，$\Delta t$取为0.1
首先空间离散，使用上面$D=\frac{1}{h}lnE$的一阶近似，得到一阶差商格式$\frac{\partial u}{\partial x}=\frac{u_{j+1}(t)-u_j(t)}{\Delta x}$时间推进仍然用单步的欧拉法。
得到离散方程
$\frac{u_j^{n+1}-u_j^n}{\Delta t}+\frac{u_{j+1}^n-u_j^n}{\Delta x}=0$
具体实现代码如下

#include 
#include 
#include 
using namespace std;
const int NE=32,//空间点数
NS=100;//时间步数
const double rb=-5,l=10,//计算域左边界，计算域长度
dt=0.1,//时间步长
dx=l/NE;
void init_guass(vector<double> &u0)//设置高斯函数初场
{
    for(int i=0;i<u0.size();i++) 
	{
		u0[i]=exp(-pow((l*double(i)/(NE-1)+rb),2));
	}
}
void advance(vector<double>& u)
{
    vector<double> t(u);
    for(int i=0;i<u.size()-1;i++)
    {
        u[i]=(1+dt/dx)*t[i]-t[i+1]*dt/dx;
    }
    int i=u.size()-1;
    u[i]=(1+dt/dx)*t[i]-t[0]*dt/dx;
}
ostream& operator<<(ostream& out,const vector<double>& A)
{
        for(int j=0;j<A.size()-1;j++)
        {
            out<<A[j]<<'\t';
        }
        out<<A[A.size()-1];
    return out;
}
int main()
{
    vector<double> u(NE+1);
    init_guass(u);
    cout<<NE+1<<'\t'<<NS<<'\t'<<rb<<'\t'<<l<<'\n';
    cout<<u<<'\n';
    for(int i=0;i<NS;i++)
    {
        advance(u);
        cout<<u<<'\n';
    }
    return 0;
}

计算结果如下

可以看到计算很快就发散了。

这里对格式做一个稳定性分析
记$u_j^n=u(x_j,t_n)$则推进公式可以写为
$u(x_j,t_n+\Delta t)=u(x_j,t_n)-\frac{\Delta t}{\Delta x}(u(x_j+\Delta x,t_n)-u(x_j,t_n))$
对$u$在空间上做傅里叶变换得到
$u=\int a(t,w)e^{jwx}dw$，$j$是虚数单位，代入推进公式得
$\int a(t+\Delta t,w)e^{jwx}dw=\int a(t,w)e^{jwx}-\frac{\Delta t}{\Delta x}(a(t,w)e^{jw(x+\Delta x)}-a(t,w)e^{jwx})dw$
得$a(t,w)$应满足的关系式为
$a(t+\Delta t,w)=a(t,w)-\frac{\Delta t}{\Delta x}(a(t,w)e^{jw\Delta x}-a(t,w))$
于是可以得到
$\frac{|a(t+\Delta t,w)|}{|a(t,w)|}=|1+\frac{\Delta t}{\Delta x}-\frac{\Delta t}{\Delta x}{e}^{jw\Delta x}|=|1+\frac{\Delta t}{\Delta x}(1-cos(w\Delta x))-jsin(w\Delta x)|>1$
可以看到以这种方式推进，总能量总是增加的，因此随着计算的推进必然是发散的。

这里同样可以通过添加人工粘性来抑制发散，不过我们换一种方法。之前使用的空间导数的离散格式是由
$D=\frac{1}{h}lnE=\frac{E-I}{h}+\cdots +\frac{(-1{)}^{n-1}(E-I{)}^n}{nh}+\cdots$
一阶近似得到的。
对其做一个简单变换可以得到一个新的离散形式
$D=-\frac{1}{h}ln{E}^{-1}=-\frac{E^{-1}-I}{h}+\cdots +\frac{(-1{)}^n(E^{-1}-I{)}^n}{nh}+\cdots$
这时我们可以得到新的一阶近似
$D=\frac{I-E^{-1}}{h}$
类似的我们还有
我们把两种$D$的展开形式相加可以得到
$2D=\frac{E-E^{-1}}{h}+\cdots +\frac{(-1{)}^n((E^{-1}-I{)}^n-(E-I{)}^n)}{nh}$
这里我们可以直接将2除到右边得到一个$D$的展开。也可以利用对数运算的性质，我们通过把$E$和$E^{-1}$分别替换成$E^{\frac{1}{2}}$和$E^{-\frac{1}{2}}$将2消去。
为了区分我们引入新的算子
$$\begin{gathered} \Delta =E-I \\ \nabla =I-E^{-1} \\ \delta =E^{\frac{1}{2}}-E^{-\frac{1}{2}} \end{gathered}$$
这三个算子分别称为前向差分、后向差分和中心差分算子。
前面发散的空间离散格式是前项差分，即计算时使用计算点前面的差分来近似计算当前点处的微分，我们现在改用后向差分，即利用计算点后面的差分代替计算当前点处的微分。
于是得到新的推进公式
$\frac{u_j^{n+1}-u_j^n}{\Delta t}+\frac{u_j^n-u_{j-1}^n}{\Delta x}=0$
于是得到新的advance函数

void advance(vector<double>& u)
{
    vector<double> t(u);
    for(int i=1;i<u.size();i++)
    {
        u[i]=t[i]-(t[i]-t[i-1])*dt/dx;
    }
    int i=0;
    u[i]=t[i]-(t[i]-t[u.size()-1])*dt/dx;
}

计算得到

可以看到使用后向差分做空间离散就不会发散了，但是会有明显的耗散作用，很快波形峰值出现了明显的降低。为什么前差和后差会有截然想法的结果？这就是迎风的问题，由于对流方程的信息传播具有方向性，我们求解的这个方程的波形是从左向右传播的，因此我们推进时任意一点的新值都应当是由其左侧点的值计算而来的，显然后向差分才符合这个要求。如果我们使用前项差分，那么所有点的新值都是由其右侧的点的值计算而来，这显然不符合微分方程所描述的特征，因此必然会出现非物理的现象，这里就表现的是计算发散。
同样利用傅里叶变换做一个稳定性分析可以得到
$\frac{|a(t+\Delta t,w)|}{|a(t,w)|}=|1-\frac{\Delta t}{\Delta x}+\frac{\Delta t}{\Delta x}{e}^{jw\Delta x}|=|1-\frac{\Delta t}{\Delta x}+\frac{\Delta t}{\Delta x}cos(w\Delta x)+jsin(w\Delta x)|$
由于$\frac{\Delta t}{\Delta x}>0$因此要满足计算稳定需满足$\frac{\Delta t}{\Delta x}\le 1$这也就是CFL数的由来。我们观察临界值$\frac{\Delta t}{\Delta x}=1$时恰好可以满足能量守恒，这时各波数能量既不增加也不减小。于是调整$\Delta t$使$\Delta t=\Delta x=\frac{10}{32}$，再次计算得

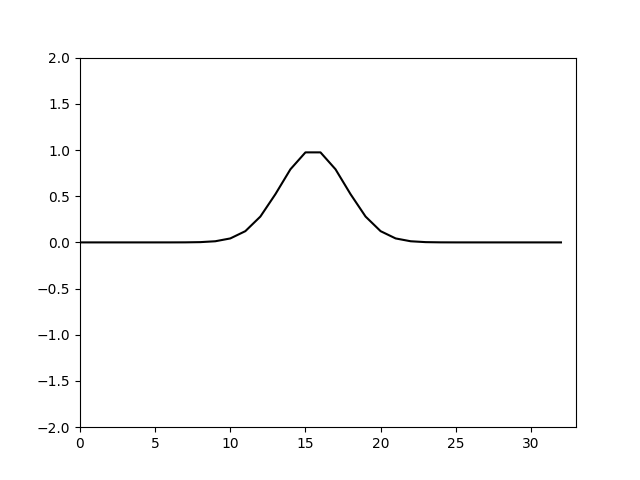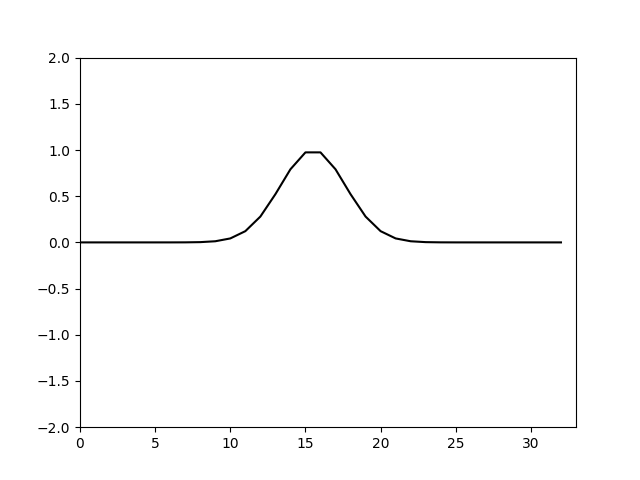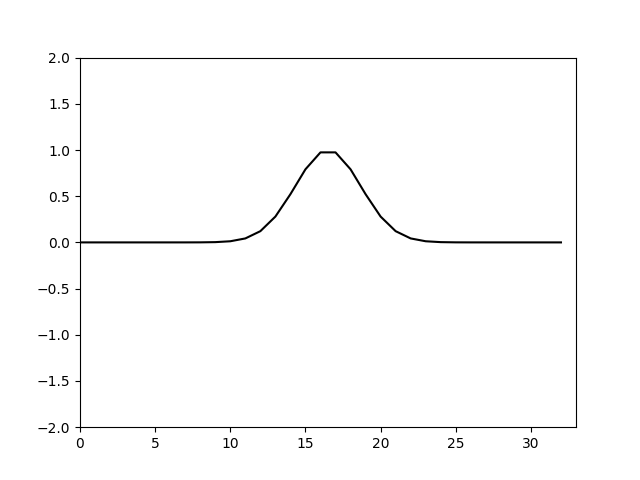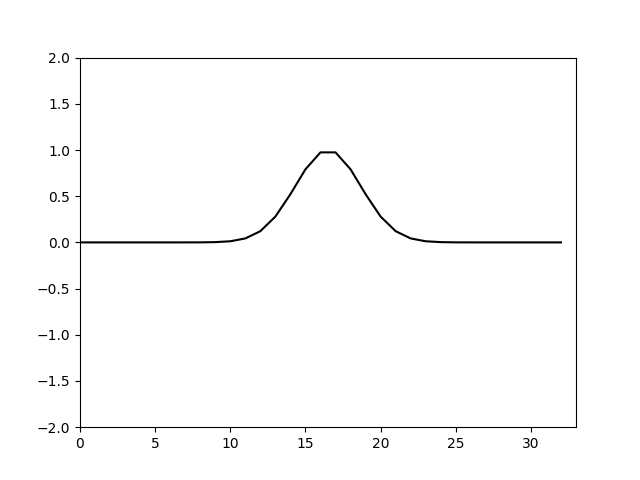
可以看到这次就没有耗散了。这是从稳定性角度分析这个格式和相应时间步长空间步长得到的结果。
我们同样可以从特征线的角度来分析这个问题，在之前的文章中有提到过这个方程的特征线。这个方程在$t-x$平面上沿着任意一条$x=C+t$的曲线，$u$的值不变，因此我们可以看到从$t$时刻开始经过任意时间$\Delta t$，在$t$时刻的$u(x)$值会跑到$x+\Delta t$的位置处，换句话说$u(x,t+\Delta t)=u(x-\Delta t,t)$，那么当$\Delta x=\Delta t$时，直接有$u_j^{n+1}=u(x,t+\Delta t)=u(x-\Delta x,t)=u_{j-1}^n$而空间后向差分，时间单步欧拉推进时如果满足$\Delta x=\Delta t$，恰好就可以化简为$u_j^{n+1}=u_{j-1}^n$所以这时其实是利用特征线的性质直接求解的方程的精确解。
从这个问题的分析也可以看到实际上格式耗散是一个和$\Delta x、\Delta t$还有离散方式都有关的量，这也是为什么前面用伪谱法和有限元时添加的人工粘性都需要试算(最正确的做法应该是利用一些分析方法计算得到，而不是试，因为复杂方程可能没有精确解，没法比对耗散大小)，而不是一个统一的值。

前面提到的前向差分、后向差分都已经试过了，现在就再试一下中心差分。利用$\frac{u_{j+1}-u_{j-1}}{2h}$代替空间导数项，时间推进同样使用欧拉单步推进。这里就不算了，直接做个稳定性分析。
前面的稳定性分析是通过频谱分析来实现的，这回换一种分析方式，利用泰勒展开来分析。
$u_j^{n+1}=u_j^n-\frac{\Delta t}{2\Delta x}(u_{j+1}^n-u_{j-1}^n)$
对两边做泰勒展开
$u+u_t^{\prime }\Delta t+\cdots +\frac{1}{n!}{u}_t^{(n)}\Delta t^n+\cdots =u-\frac{\Delta t}{2\Delta x}(u+u_x^{\prime }\Delta x+\cdots +\frac{1}{n!}{u}_x^{(n)}\Delta x^n+\cdots -u+u_x^{\prime }\Delta x+\cdots +\frac{1}{n!}{u}_x^{(n)}(-\Delta x{)}^n)+\cdots$
高阶项全部作为截断误差抹去，仅保留到二阶得
$u+u_t\Delta t+\frac{1}{2}{u}_{tt}\Delta t^2=u-u_x\Delta t$
整理一下得
$u_t+u_x=-\frac{1}{2}{u}_{tt}\Delta t$
对差分形式做泰勒展开得到的微分方程在原方程的基础上多出来一个$u_{tt}$这一项，这一项是数值格式的最低阶截断误差，是个二阶导数项，表现耗散作用。其耗散系数$\nu =-\frac{1}{2}\Delta t$是个负数，所以其最终在求解中的作用是一个反耗散(使得计算域内总能量不断增大)，并且$\Delta t$越大这种反耗散越明显，计算发散的越快。所以这个格式是不稳定的，需要添加人工粘性抵消这个由时间推进带来的反耗散作用。对于泰勒展开得到的这个方程的右端项，我们通常称为格式粘性。
观察上面泰勒展开的结果，我们可以发现当使用中心差分这种系数中心对称的格式时，其泰勒展开后偶数阶空间导数项均会被消去，仅留下奇数阶空间导数项。其中偶数阶导数项对应耗散作用，奇数阶导数项对应色散作用，所以中心差分格式是没有耗散误差，仅有色散误差的。格式的反耗散完全来自显式时间推进，如果使用隐式时间推进就可以得到一个正的耗散作用，格式就稳定了，这也是为什么通常我们都认为隐式格式比显式格式更加稳定。

由于格式粘性项相当于差分方程的最低阶误差，因此这个格式是一阶格式。由于这个误差仅由时间步长决定，因此使用更高阶的时间推进格式即可提高格式的整体精度，但是前面提到显式时间推进永远是反耗散作用，不可能稳定。因此这个格式必须要像前面的方法一样使用人工粘性，但是如果使用二阶人工粘性，由于人工粘性本身需要调节粘性项系数，如果不能正确标定系数，那么这个人工粘性项同样相当于引入的额外误差，因此格式精度就不会超过二阶(经典的Lax-Wendroff格式就可以看做是标定人工粘性系数为$\frac{|f^{\prime }(u)|\Delta x}{2}$的中心差分格式，因为粘性项本身是二阶的，粘性系数又有带有$\Delta x$因此其空间精度为二阶)。要想获得高阶格式就需要使用高阶的人工粘性并分析格式粘性尽可能保证格式粘性的阶数足够高。

Burgers方程

利用有限差分法求解
$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$
初场为$u_0(x)=e^{-x^2}，x\in [-5,5]$周期边界
$u_j^{n+1}=u_j^n-\frac{\Delta t}{\Delta x}{u}_j^n(u_j^n-u_{j-1}^n)$
得到新的advance函数如下，在函数中加了人工粘性

void advance(vector<double>& u)
{
    vector<double> t(u);
    for(int i=1;i<u.size()-1;i++)
    {
        u[i]=t[i]-t[i]*(t[i]-t[i-1])*dt/dx;
    }
    int i=0;
    u[i]=t[i]-t[i]*(t[i]-t[u.size()-1])*dt/dx;
    i=u.size()-1;
    u[i]=t[i]-t[i]*(t[i]-t[i-1])*dt/dx;
}

计算结果如下

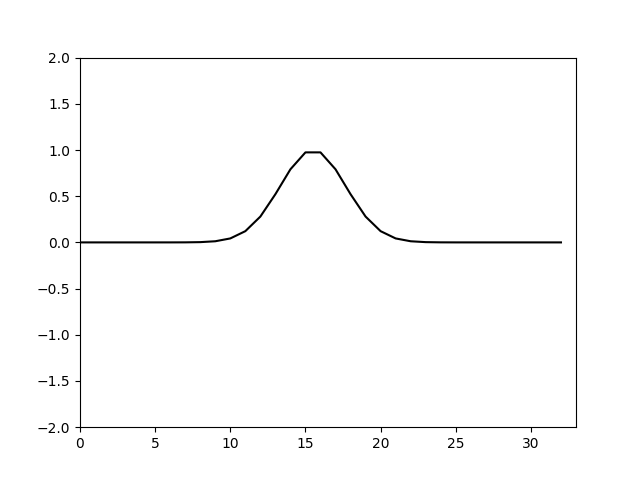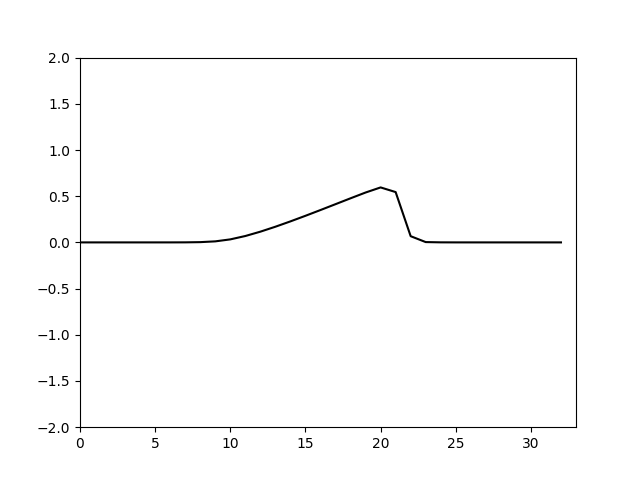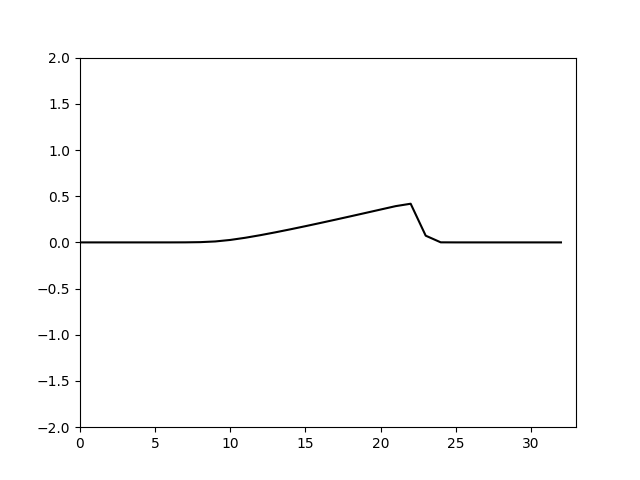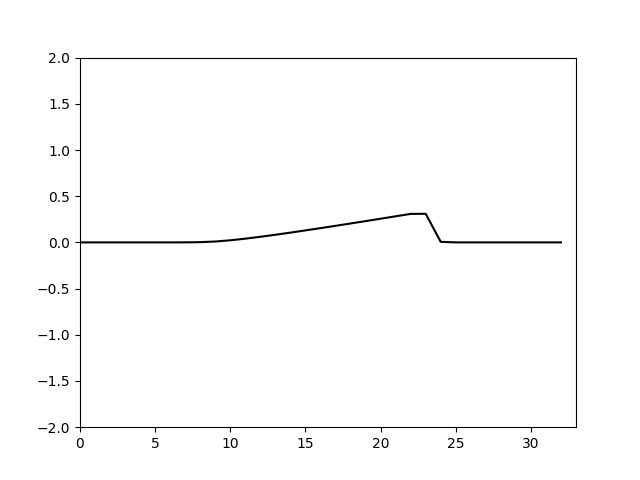
可以看到计算基本正确，但是也可以看到其实计算的耗散还是比较大的.
同样做泰勒展开，保留二阶项得
$u_t+u(u_x)=\frac{1}{2}((u_{xx}{)}^{\prime \prime }\Delta x-(u_{tt}{)}^{\prime \prime }\Delta t)$
可以看到当$\Delta x>\Delta t$是格式的粘性是正的，计算稳定，并且$\Delta x-\Delta t$越大，粘性越大由于这里取的是$\Delta x=\frac{10}{32},\Delta t=0.1$耗散偏大。仿照上面的特征线法的设置，令$\Delta t=\Delta x=\frac{10}{32}$。计算结果如下

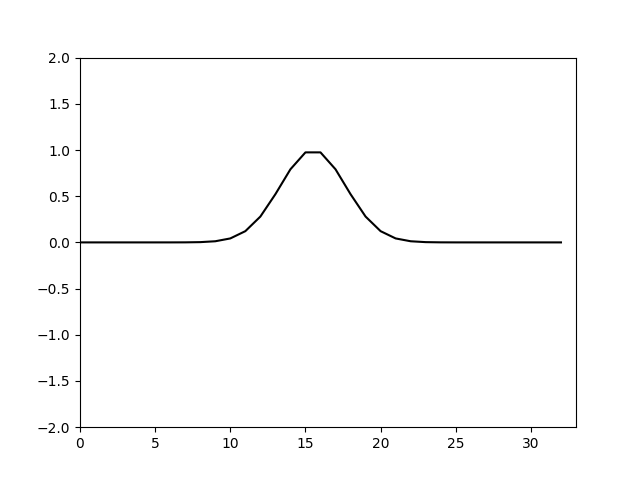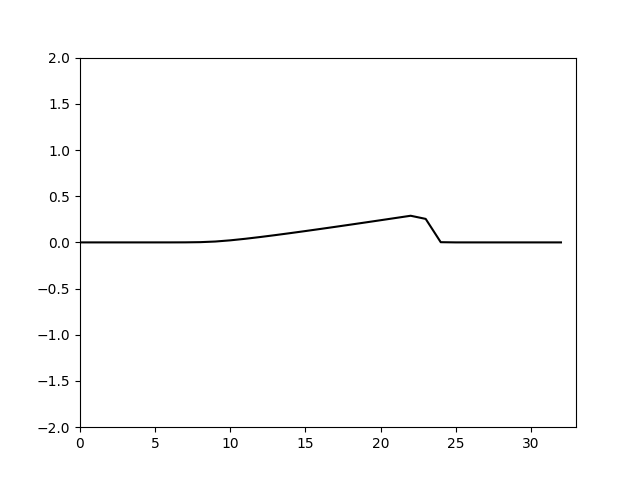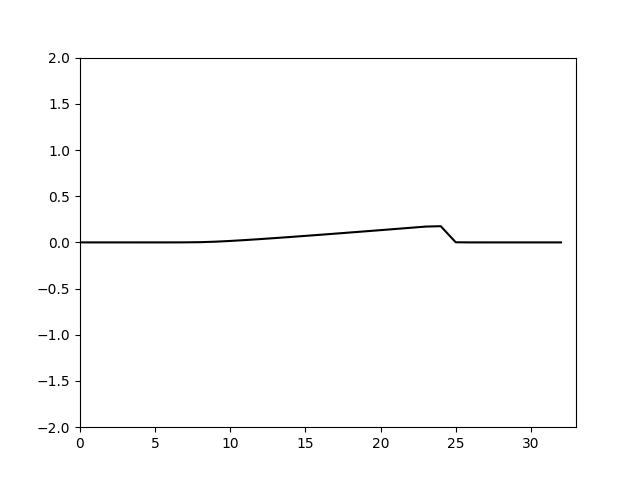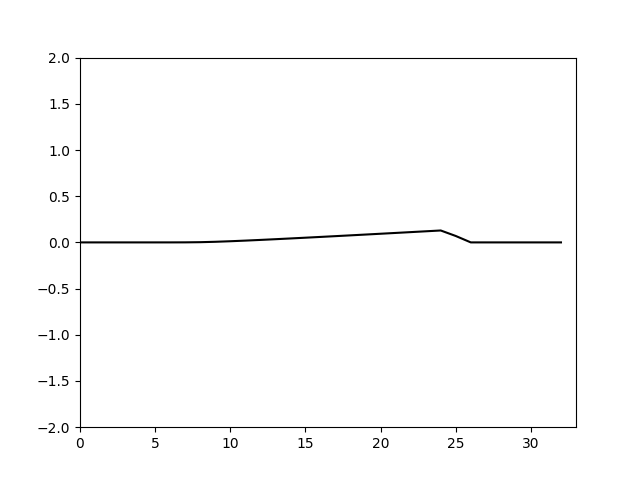
这里由于我做动图时把各个时间步的图片的显示时间保持不变，因此缩小计算时的时间步长动图就会变快，这里表面上看其实格式的粘性变化不大。这是因为格式粘性是$\frac{1}{2}((u_{xx}{)}^{\prime \prime }\Delta x-(u_{tt}{)}^{\prime \prime }\Delta t)$这是和$u$的二阶时间和空间导数相关的值。这说明想要降低耗散可能缩小$\Delta x$或提高空间离散精度(如使用更高阶的空间离散格式)更加合适。

一些其它问题

前面的伪谱法、有限元和这里的差分法基本就是CFD最常用的方法了，也是偏微分方程数值求解的基本方法。我们通常还会听到的诸如有限体积法、通量重构等方法虽然和差分法有一定的区别但通常都算在差分法中。这是CFD中应用最广泛的算法，目前应用广泛的商业软件fluent，以及star-ccm都是使用的有限体积法。但是一般的差分方法尤其是有限体积法存在一个比较大的问题就是高阶格式难以实现。

结合前面伪谱法和有限元的构造，我们可以看到。伪谱法每增加一个网格点就可以将精度提高一阶，因此这是最容易获得高阶格式的一种算法，但是这个算法很大的问题是计算域必须规则或者可以通过一些不算很复杂的空间变换变成规则计算域，否则谱系数不好求，而且边界条件也受到基函数的限制，例如我使用的三角函数就是自带周期的边界，如果计算域边界不是周期的三角函数就不能做基函数了，而需要其他的基函数来处理。

有限元方法相比于谱方法其计算更加灵活，每个单元相互独立，需要高阶形式只需要增加单元内的网格点数即可，不太需要额外的操作。但是不知道为什么这个算法在CFD中应用不是很广泛，或者说相应的商业软件名气不大。不过从我给的代码量也能看出来这个算法确实不是太好实现(我那个代码还是偷了懒少写了很多东西，导致网格只能是长度一致的一维单元)。

有限差分法构造简单，易于理解尤其是商业软件热衷的有限体积法更是如此。但是有限差分法最大的问题在于只能计算结构网格(这里仅指通常意义上的有限差分，通量重构和有限体积法可以使用非结构)高阶格式的边界处理繁琐。因为差分法要得到高阶格式就意味着每一个点的推进都需要两侧更多的点的值。在计算域内部这没有任何问题，因为计算域内部不论哪个点周围的点都多得是，想用几个用几个。但是在计算域边界上就不一样了，边界以外就没有点了。要使用保证相同的阶数仍然需要相同数量的点，那就需要构造新的差分格式。一阶二阶无所谓最多也构造一两个新格式，但是更高阶就相当麻烦，尤其是编程实现非常繁琐。而且边界上采用不同的格式还会涉及到一个格式匹配的问题，边界格式设计的不好可能还有发散的问题。我们可以看到fluent仅提供了二阶精度。想要利用fluent获得高精度的结果只有增加网格量一条路，使用fluent想要不改变网格量利用格式阶数来提高计算精度是不可能的。fluent因为使用的是有限体积法，这种方法比一般的差分更难构造稳定的高阶格式，尤其是非结构网格情况下，光是搜索关联网格数据都很费劲了。后面我会给一个计算气动声学(CAA)中常用的差分格式——频散关系保持(DRP)格式，经典DRP格式需要7个网格点(理论上是6阶精度)，周期边界的一维代码写起来就有点麻烦了，CAA中常用的无反射边界用7个点写那才叫头疼，因此有时候直接通过边界降阶来简化边界条件实现(当年做作业写了个9点的头都晕了，本来一开始是做的11点格式，最后边界实在处理不了就改成9点了)。