对抗样本生成算法之BIM算法
目录
- 论文主要内容
- BIM算法原理
- ILCM算法原理
- 实验效果
- 物理世界实验
论文 2017ICLR-Adversarial Examples in the physical world.
论文主要内容
- 提出了BIM攻击算法,即迭代FGSM(I-FGSM)算法
- 提出ILCM最相似迭代算法(Iterative Least-likely Class Method)
- 进行实验,验证了在真实物理环境中,通过图像采集得到的对抗样本是否依旧能够使得分类器分类错误。
相对于FGSM的单步攻击,I-FGSM分多步添加噪声,更能拟合模型参数,因此通常表现出比FGSM更强的白盒能力。
BIM算法原理
FGSM里面,每次寻找对抗样本的时候,直接是 x + ϵ ∗ s i g n ( ∇ x J ( x , y ) ) x+\epsilon*sign(∇_xJ(x,y)) x+ϵ∗sign(∇xJ(x,y)),这样是把每个像素点都变化了 ϵ \epsilon ϵ 这么大。这个改动其实是挺大,因为每个像素点都动了。
FGSM提出的理论假设:假设目标损失函数 J ( x , y ) J(x,y) J(x,y)与 x x x之间是近似线性的,即 J ( x , y ) ≈ w T x J(x,y)≈w^Tx J(x,y)≈wTx,然后我们想往 x x x加上一个小的扰动 η \eta η,使得 J ( x , y ) J(x,y) J(x,y)变化最大。而 J ( x + η , y ) − J ( x , y ) ≈ w T η J(x+\eta,y)−J(x,y)≈w^T\eta J(x+η,y)−J(x,y)≈wTη,要使最大,最好是直接 η = ϵ ∗ s i g n ( ∇ x J ( x , y ) ) \eta=\epsilon*sign(∇_xJ(x,y)) η=ϵ∗sign(∇xJ(x,y))。
然而,这个线性假设不一定正确,如果 J J J和 x x x不是线性的,那么在 ( 0 , ϵ ∗ s i g n ( ∇ x J ( x , y ) ) ) (0,\epsilon*sign(∇_xJ(x,y))) (0,ϵ∗sign(∇xJ(x,y)))之间是否存在某个扰动,使得 J J J增加的也很大,此时 x x x的修改量就可以小于 ϵ \epsilon ϵ。
于是,作者就提出迭代的方式来找各个像素点的扰动,而不是一次性所有像素都改那么多,即迭代式的FGSM,也就是I-FGSM(Iterative FGSM)或BIM(Basic Iterative Method)。公式如下:
迭代的含义:每次在上一步的对抗样本的基础上,各个像素增长 α \alpha α(或者减少),然后再执行裁剪,保证新样本的各个像素都在 x x x的 ϵ \epsilon ϵ 邻域内。这种迭代的方法是有可能在各个像素变化小于 ϵ \epsilon ϵ 的情况下找到对抗样本的,如果找不到,最差的效果就跟原始的FGSM一样。
裁剪(Clip):在迭代更新过程中,随着迭代次数的增加,样本的部分像素值可能会溢出,比如超出0到1的范围,这时需将这些值用0或1代替,最后才能生成有效的图像。该过程确保了新样本的各个像素在原样本各像素的某一领域内,不至于图像失真。
ILCM算法原理
该算法是I-FGSM的难度升级版,将输入图像分类成原本最不可能分到的类别,公式如下所示。原本No-targeted Attacks只需要让模型分类错误就算攻击成功,而现在需要模型将攻击图像分类成原本分类概率极低的类别,难度可想而知。当然,这部分内容其实是有Targeted Attacks的雏形,因为可以指定攻击类别。从公式中可以看到和前面无目标攻击公式的最大区别在于 α \alpha α前面的加号变成减号,同时原本的真实标签 y t r u e y_{true} ytrue变成 y L L y_{LL} yLL,这2个修改使得模型优化的目标是最终对应类别为 y L L y_{LL} yLL的分类概率越来越大,这和常规的分类模型训练类似,只不过监督信息并不是真实标签,而是指定的一个标签。
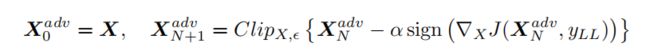
这个 y L L y_{LL} yLL是原输入图像在分类模型中分类概率最小的类别,可以通过如下式子计算得到:
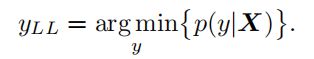
实验效果
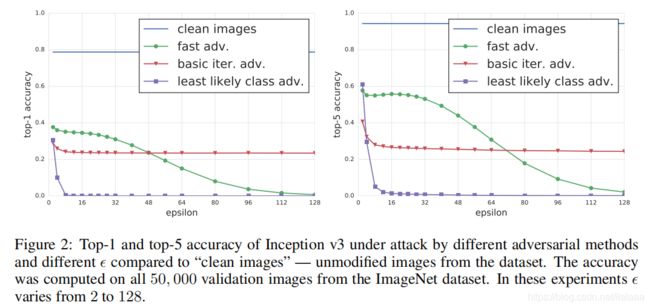
当 ϵ \epsilon ϵ比较小的,I-FGSM的攻击效果比原始的FGSM好,而且ILCM的攻击效果最好,从图片上也能看出ILCM的改动是最小的。
物理世界实验
以往在机器学习的对抗样本研究都是直接在图像本身上研究的。生成的对抗样本通过直接调用API输入到DNN中。然而,在现实中,图像都是基于感光设备采集的。在其生成图像时,由于光线的影响、摄像头位置的影响等等,使得引入噪声,造成攻击者千方百计在图像中添加的微小干扰被破坏掉。
作者直接对对抗图片进行拍照,让模型对拍照结果进行分类,观察被照相机拍照后是否还具有对抗效果。
实验步骤:
- 使用ImageNet训练一个Inception V3网络。
- 寻找验证集里面特定样本的对抗样本(使用不同的对抗方法以及不同的 ϵ \epsilon ϵ)
- 把原始样本和对抗样本打印出来,并用手机拍这些打印出来的图片,图片有二维码定位用。
- 使用Inception V3模型识别手机拍出来的图片。
实验结果:
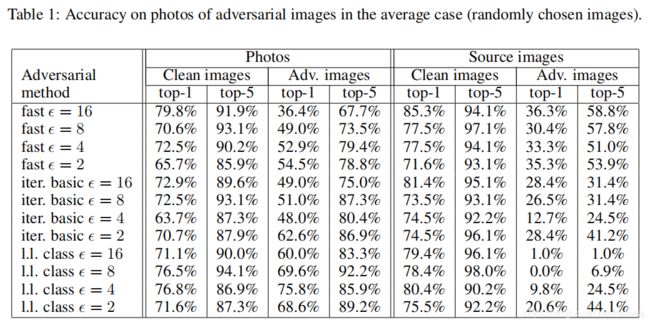
作者把这种感光设备采集图像中引入噪声的过程叫做 photo transformation,然后这些transformation又可以看作是改变光照、模糊、加入噪声的这些子变化的合成,并做实验量化这些transformation的影响。
从表中可以看到,Photo Transformation对对抗样本的对抗性有一定的损失作用。其中FGSM的影响相对比较小,因为FGSM改动大。而对I-FGSM的影响比较大,这是因为它们的扰动值更小,比较容易被破坏。