有限体积法(3)——一维扩散方程数值求解(第一类边界条件)
例1:无热源导热
考虑一根细棒的导热问题,假设截面内温度均匀,问题简化为一维稳态导热问题,控制方程为
d d x ( k d T d x ) = 0 \frac{d}{dx} \left( k \frac{dT}{dx} \right) =0 dxd(kdxdT)=0
棒两端边界是恒温边界条件, T A = 100 ℃ T_A=100℃ TA=100℃, T B = 500 ℃ T_B=500℃ TB=500℃。导热系数 k = 1000 W / m . K k=1000 W/m.K k=1000W/m.K,长度 L = 0.5 m L=0.5m L=0.5m,截面面积 A = 0.01 m 2 A=0.01 m^2 A=0.01m2,棒内无热源。

划分网格
首先将计算域均匀划分为5个网格单元,设棒的长度方向为x轴,则节点间距 δ x = 0.1 m \delta x = 0.1m δx=0.1m。如下图所示,网格单元1和网格单元5都包含一个计算域的边界。

内部网格
对于内部节点2、3和4,根据一维扩散方程推导 中式 ( 9 ) − ( 11 ) (9)-(11) (9)−(11)可知,其离散方程的形式如下,
a P ϕ P = a W ϕ W + a E ϕ E + S u (1a) a_P \phi_P = a_W \phi_W + a_E \phi_E + S_u \tag{1a} aPϕP=aWϕW+aEϕE+Su(1a)
也可以写成
− a W ϕ W + a P ϕ P − a E ϕ E = S u (1b) -a_W \phi_W + a_P \phi_P -a_E \phi_E= S_u \tag{1b} −aWϕW+aPϕP−aEϕE=Su(1b)
系数,
a W = Γ w A w δ x W P a E = Γ e A e δ x P E a P = a W + a E − S P } (2) \left. \begin{aligned} a_W=&\frac{\Gamma_w A_w}{\delta x_{WP}} \\ \\ a_E=&\frac{\Gamma_e A_e}{\delta x_{PE}} \\ \\ a_P =& a_W + a_E - S_P \end{aligned} \right \} \tag{2} aW=aE=aP=δxWPΓwAwδxPEΓeAeaW+aE−SP⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(2)
本例中,扩散系数 Γ \Gamma Γ 即导热系数 k k k, 截面面积 A w = A e = A A_w = A_e = A Aw=Ae=A ,网格间距 δ x W P = δ x P E = δ x \delta x_{WP} = \delta x_{PE} = \delta x δxWP=δxPE=δx, 源项 S u = 0 , S P = 0 S_u = 0 , S_P = 0 Su=0,SP=0。 以节点2为例,其离散方程为
a 2 , 2 T 2 = a 2 , 1 T 1 + a 2 , 3 T 3 (3a) a_{2,2} T_2 = a_{2,1} T_1 + a_{2,3} T_3 \tag{3a} a2,2T2=a2,1T1+a2,3T3(3a)
即
− a 2 , 1 T 1 + a 2 , 2 T 2 − a 2 , 3 T 3 = 0 (3b) -a_{2,1} T_1 +a_{2,2} T_2 -a_{2,3} T_3= 0 \tag{3b} −a2,1T1+a2,2T2−a2,3T3=0(3b)
各系数为,
a 2 , 1 = k A δ x a 2 , 3 = k A δ x a 2 , 2 = a 2 , 1 + a 2 , 3 } (4) \left. \begin{aligned} a_{2,1} =& \frac{k A}{\delta x} \\ \\ a_{2,3} =& \frac{k A}{\delta x} \\ \\ a_{2,2}=& a_{2,1} + a_{2,3} \end{aligned} \right \} \tag{4} a2,1=a2,3=a2,2=δxkAδxkAa2,1+a2,3⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(4)
边界网格
节点 1
对于节点1,其边界面w就是计算域的A边界,所以w边界上的梯度不能再用中心差分格式计算,可以采用单边差分格式,方程离散为
k A ( T E − T P δ x ) − k A ( T P − T A δ x / 2 ) = 0 (5a) kA\left( \frac{T_E - T_P}{\delta x} \right) - kA\left( \frac{T_P - T_A}{\delta x / 2} \right) = 0 \tag{5a} kA(δxTE−TP)−kA(δx/2TP−TA)=0(5a)
即
k A ( T 2 − T 1 δ x ) − k A ( T 1 − T A δ x / 2 ) = 0 (5b) kA\left( \frac{T_2 - T_1}{\delta x} \right) - kA\left( \frac{T_1 - T_A}{\delta x / 2} \right) = 0 \tag{5b} kA(δxT2−T1)−kA(δx/2T1−TA)=0(5b)
整理成
( k A δ x + 2 k A δ x ) T 1 = 0 × T 0 + ( k A δ x ) T 2 + ( 2 k A δ x ) T A (6) \left( \frac{kA}{\delta x} + \frac{2kA}{\delta x} \right) T_1 = 0 \times T_0 + \left( \frac{kA}{\delta x} \right) T_2 + \left( \frac{2kA}{\delta x} \right) T_A \tag{6} (δxkA+δx2kA)T1=0×T0+(δxkA)T2+(δx2kA)TA(6)
所以节点1的离散方程为
− a 1 , 0 T 0 + a 1 , 1 T 1 − a 1 , 2 T 2 = S u , 1 (7) -a_{1,0} T_0 +a_{1,1} T_1 -a_{1,2} T_2= S_{u,1} \tag{7} −a1,0T0+a1,1T1−a1,2T2=Su,1(7)
其中,
a 1 , 0 = 0 a 1 , 2 = k A δ x a 1 , 1 = a W + a E − S P S P , 1 = − 2 k A δ x S u , 1 = 2 k A δ x T A } (8) \left. \begin{aligned} a_{1,0} =&0 \\ \\ a_{1,2} =& \frac{kA}{\delta x} \\ \\ a_{1,1} =& a_W + a_E - S_P \\ \\ S_{P,1} =& - \frac{2kA}{\delta x} \\ \\ S_{u,1} =& \frac{2kA}{\delta x} T_A \end{aligned} \right \} \tag{8} a1,0=a1,2=a1,1=SP,1=Su,1=0δxkAaW+aE−SP−δx2kAδx2kATA⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(8)
节点5
与节点1类似,节点5的e边界面即计算域的B边界,其方程离散为
k A ( T B − T P δ x / 2 ) − k A ( T P − T W δ x ) = 0 (9a) kA\left( \frac{T_B - T_P}{\delta x /2} \right)- kA\left( \frac{T_P - T_W}{\delta x} \right)=0 \tag{9a} kA(δx/2TB−TP)−kA(δxTP−TW)=0(9a)
即
k A ( T B − T 5 δ x / 2 ) − k A ( T 5 − T 4 δ x ) = 0 (9b) kA\left( \frac{T_B - T_5}{\delta x /2} \right)- kA\left( \frac{T_5 - T_4}{\delta x} \right)=0 \tag{9b} kA(δx/2TB−T5)−kA(δxT5−T4)=0(9b)
整理为
( k A δ x + 2 k A δ x ) T 5 = ( k A δ x ) T 4 + 0 × T 6 + ( 2 k A δ x ) T B (10) \left( \frac{kA}{\delta x} + \frac{2kA}{\delta x} \right) T_5 = \left( \frac{kA}{\delta x} \right) T_4+ 0 \times T_6+ \left( \frac{2kA}{\delta x} \right) T_B \tag{10} (δxkA+δx2kA)T5=(δxkA)T4+0×T6+(δx2kA)TB(10)
即,
− a 5 , 4 T 4 + a 5 , 5 T 5 − a 5 , 6 T 6 = S u , 5 (11) -a_{5,4} T_4 +a_{5,5} T_5 -a_{5,6} T_6= S_{u,5} \tag{11} −a5,4T4+a5,5T5−a5,6T6=Su,5(11)
其中,
a 5 , 4 = k A δ x a 5 , 6 = 0 a 5 , 5 = a W + a E − S P S P , 5 = − 2 k A δ x S u , 5 = 2 k A δ x T B } (12) \left. \begin{aligned} a_{5,4} =&\frac{kA}{\delta x} \\ \\ a_{5,6} =&0 \\ \\ a_{5,5} =& a_W + a_E - S_P \\ \\ S_{P,5} =& - \frac{2kA}{\delta x} \\ \\ S_{u,5} =& \frac{2kA}{\delta x} T_B \end{aligned} \right \} \tag{12} a5,4=a5,6=a5,5=SP,5=Su,5=δxkA0aW+aE−SP−δx2kAδx2kATB⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(12)
然后把5个网格节点的离散方程集合成一个线性方程组,
{ a 1 , 1 T 1 − a 1 , 2 T 2 = S u , 1 − a 2 , 1 T 1 + a 2 , 2 T 2 − a 2 , 3 T 3 = 0 − a 3 , 2 T 2 + a 3 , 3 T 3 − a 3 , 4 T 4 = 0 − a 4 , 3 T 3 + a 4 , 4 T 4 − a 4 , 5 T 5 = 0 − a 5 , 4 T 4 + a 5 , 5 T 5 = S u , 5 (13) \left\{ \begin{aligned} a_{1,1} T_1 - a_{1,2} T_2 = S_{u,1} \\ \\ -a_{2,1} T_1 + a_{2,2} T_2 -a_{2,3} T_3 = 0 \\ \\ -a_{3,2} T_2 + a_{3,3} T_3 -a_{3,4} T_4 = 0 \\ \\ -a_{4,3} T_3 + a_{4,4} T_4 -a_{4,5} T_5 = 0 \\ \\ -a_{5,4} T_4 + a_{5,5} T_5 = S_{u,5} \end{aligned} \right. \tag{13} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧a1,1T1−a1,2T2=Su,1−a2,1T1+a2,2T2−a2,3T3=0−a3,2T2+a3,3T3−a3,4T4=0−a4,3T3+a4,4T4−a4,5T5=0−a5,4T4+a5,5T5=Su,5(13)
写出矩阵形式就是
[ a 1 , 1 a 1 , 2 0 0 0 a 2 , 1 a 2 , 2 a 2 , 3 0 0 0 a 3 , 2 a 3 , 3 a 3 , 4 0 0 0 a 4 , 3 a 4 , 4 a 4 , 5 0 0 0 a 5 , 4 a 5 , 5 ] [ T 1 T 2 T 3 T 4 T 5 ] = [ S u , 1 0 0 0 S u , 5 ] (14) \left [ \begin{matrix} a_{1,1} &a_{1,2} &0 &0 &0 \\ a_{2,1} &a_{2,2} &a_{2,3} &0 &0 \\ 0 &a_{3,2} &a_{3,3} &a_{3,4} &0 \\ 0 &0 &a_{4,3} &a_{4,4} &a_{4,5} \\ 0 &0 &0 &a_{5,4} &a_{5,5} \end{matrix} \right ] \left [ \begin{matrix} T_1 \\ T_2 \\ T_3 \\ T_4 \\ T_5 \end{matrix} \right ] = \left [ \begin{matrix} S_{u,1} \\0 \\ 0\\0 \\ S_{u,5} \end{matrix} \right ] \tag{14} ⎣⎢⎢⎢⎢⎡a1,1a2,1000a1,2a2,2a3,2000a2,3a3,3a4,3000a3,4a4,4a5,4000a4,5a5,5⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡T1T2T3T4T5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡Su,1000Su,5⎦⎥⎥⎥⎥⎤(14)
然后代入数值,求解方程组,得
[ T 1 T 2 T 3 T 4 T 5 ] = [ 140 220 300 380 460 ] (15) \left [ \begin{matrix} T_1 \\ T_2 \\ T_3 \\ T_4 \\ T_5 \end{matrix} \right ]= \left [ \begin{matrix} 140 \\ 220 \\ 300 \\ 380 \\ 460 \end{matrix} \right ] \tag{15} ⎣⎢⎢⎢⎢⎡T1T2T3T4T5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡140220300380460⎦⎥⎥⎥⎥⎤(15)
与该问题的解析解 T = 800 x + 100 T=800x+100 T=800x+100 对比如下图,

例2:有热源导热
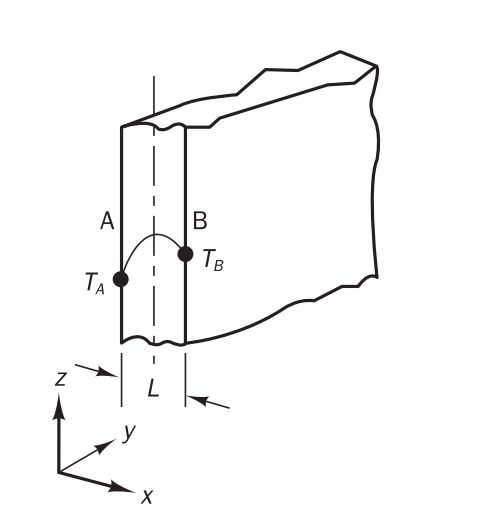
考虑一块截面面积较大的平板,截面内温度均匀,两边界面A和B为恒温边界,可以将其视为在平板厚度上的一维导热问题,与例1不同的是内部有均匀热源q,如上图所示。该模型的参数:厚度 L = 2 c m L=2 cm L=2cm, 导热系数为常数 k = 0.5 W / m . K k = 0.5 W/m.K k=0.5W/m.K,内部热源 q = 1000 k W / m 3 q=1000 kW/m^3 q=1000kW/m3,边界条件 T A = 100 ℃ , T B = 200 ℃ T_A = 100 ℃ ,T_B=200 ℃ TA=100℃,TB=200℃。
控制方程仅比例1中多了源项,
d d x ( k d T d x ) + q = 0 (16) \frac{d}{dx} \left( k \frac{dT}{dx} \right) + q =0 \tag{16} dxd(kdxdT)+q=0(16)
网格划分
网格筒例1,假设厚度方向为x轴,计算域分为5个网格单元,则网格尺寸 δ x = 0.004 m \delta x =0.004 m δx=0.004m,y-z平面的截面取单位面积,即 A = 1 m 2 A=1 m^2 A=1m2。
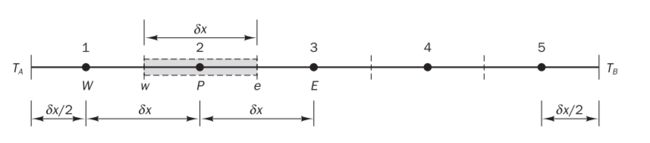
内部网格
对于内部节点2,3,4 其方程离散为,
[ ( k A d T d x ) e − ( k A d T d x ) w ] + q Δ V = 0 (17) \left [ \left ( kA\frac{dT}{dx} \right )_e -\left ( kA\frac{dT}{dx} \right )_w \right] + q \Delta V =0 \tag{17} [(kAdxdT)e−(kAdxdT)w]+qΔV=0(17)
[ k A ( T E − T P δ x ) − k A ( T P − T W δ x ) ] + q A δ x = 0 (18) \left [ kA\left ( \frac{T_E - T_P}{\delta x} \right ) - kA\left ( \frac{T_P - T_W}{\delta x} \right ) \right] + q A \delta x =0 \tag{18} [kA(δxTE−TP)−kA(δxTP−TW)]+qAδx=0(18)
然后整理一下,
( k A δ x + k A δ x ) T P = k A δ x T W + k A δ x T E + q A δ x (19) \left( \frac{kA}{\delta x} +\frac{kA}{\delta x} \right) T_P = \frac{kA}{\delta x} T_W + \frac{kA}{\delta x} T_E + qA\delta x \tag{19} (δxkA+δxkA)TP=δxkATW+δxkATE+qAδx(19)
即,
a P ϕ P = a W ϕ W + a E ϕ E + S u (20a) a_P \phi_P = a_W \phi_W + a_E \phi_E + S_u \tag{20a} aPϕP=aWϕW+aEϕE+Su(20a)
或,
− a W ϕ W + a P ϕ P − a E ϕ E = S u (20a) -a_W \phi_W +a_P \phi_P -a_E \phi_E= S_u \tag{20a} −aWϕW+aPϕP−aEϕE=Su(20a)
系数为,
a W = k A δ x a E = k A δ x S P = 0 S u = q A δ x a P = a W + a E − S P } (21) \left. \begin{aligned} a_W&= \frac{kA}{\delta x} \\ \\ a_E&= \frac{kA}{\delta x} \\ \\ S_P&=0 \\ \\ S_u&= qA \delta x \\ \\ a_P&=a_W+a_E -S_P\\ \\ \end{aligned} \right \} \tag{21} aWaESPSuaP=δxkA=δxkA=0=qAδx=aW+aE−SP⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(21)
与式 ( 3 ) 、 ( 4 ) (3)、(4) (3)、(4)相比,这里的差别就是 S u S_u Su项不再是 0 0 0.
边界网格
节点 1
方程离散为,
[ k A ( T 2 − T 1 δ x ) − k A ( T 1 − T A δ x / 2 ) ] + q A δ x = 0 (22) \left [ kA\left ( \frac{T_2 - T_1}{\delta x} \right ) - kA\left ( \frac{T_1 - T_A}{\delta x /2} \right ) \right] + q A \delta x =0 \tag{22} [kA(δxT2−T1)−kA(δx/2T1−TA)]+qAδx=0(22)
整理之,
− a 1 , 0 T 0 + a 1 , 1 T 1 − a 1 , 2 T 2 = S u , 1 (23) -a_{1,0} T_0 +a_{1,1} T_1 -a_{1,2} T_2= S_{u,1} \tag{23} −a1,0T0+a1,1T1−a1,2T2=Su,1(23)
a 1 , 0 = 0 a 1 , 2 = k A δ x a 1 , 1 = a W + a E − S P S P , 1 = − 2 k A δ x S u , 1 = 2 k A δ x T A + q A δ x } (24) \left. \begin{aligned} a_{1,0} =&0 \\ \\ a_{1,2} =& \frac{kA}{\delta x} \\ \\ a_{1,1} =& a_W + a_E - S_P \\ \\ S_{P,1} =& - \frac{2kA}{\delta x} \\ \\ S_{u,1} =& \frac{2kA}{\delta x} T_A + qA\delta x \end{aligned} \right \} \tag{24} a1,0=a1,2=a1,1=SP,1=Su,1=0δxkAaW+aE−SP−δx2kAδx2kATA+qAδx⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(24)
与式 ( 7 ) 、 ( 8 ) (7)、(8) (7)、(8)相比,仅 S u , 1 S_{u,1} Su,1项多了热源项。所以,节点5也类似。
节点 5
− a 5 , 4 T 4 + a 5 , 5 T 5 − a 5 , 6 T 6 = S u , 5 (25) -a_{5,4} T_4 +a_{5,5} T_5 -a_{5,6} T_6= S_{u,5} \tag{25} −a5,4T4+a5,5T5−a5,6T6=Su,5(25)
其中,
a 5 , 4 = k A δ x a 5 , 6 = 0 a 5 , 5 = a W + a E − S P S P , 5 = − 2 k A δ x S u , 5 = 2 k A δ x T B + q A δ x } (26) \left. \begin{aligned} a_{5,4} =&\frac{kA}{\delta x} \\ \\ a_{5,6} =&0 \\ \\ a_{5,5} =& a_W + a_E - S_P \\ \\ S_{P,5} =& - \frac{2kA}{\delta x} \\ \\ S_{u,5} =& \frac{2kA}{\delta x} T_B + qA \delta x \end{aligned} \right \} \tag{26} a5,4=a5,6=a5,5=SP,5=Su,5=δxkA0aW+aE−SP−δx2kAδx2kATB+qAδx⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫(26)
整个方程组就是,
[ a 1 , 1 a 1 , 2 0 0 0 a 2 , 1 a 2 , 2 a 2 , 3 0 0 0 a 3 , 2 a 3 , 3 a 3 , 4 0 0 0 a 4 , 3 a 4 , 4 a 4 , 5 0 0 0 a 5 , 4 a 5 , 5 ] [ T 1 T 2 T 3 T 4 T 5 ] = [ S u , 1 S u , 2 S u , 3 S u , 4 S u , 5 ] (27) \left [ \begin{matrix} a_{1,1} &a_{1,2} &0 &0 &0 \\ a_{2,1} &a_{2,2} &a_{2,3} &0 &0 \\ 0 &a_{3,2} &a_{3,3} &a_{3,4} &0 \\ 0 &0 &a_{4,3} &a_{4,4} &a_{4,5} \\ 0 &0 &0 &a_{5,4} &a_{5,5} \end{matrix} \right ] \left [ \begin{matrix} T_1 \\ T_2 \\ T_3 \\ T_4 \\ T_5 \end{matrix} \right ] = \left [ \begin{matrix} S_{u,1} \\S_{u,2} \\ S_{u,3}\\S_{u,4} \\ S_{u,5} \end{matrix} \right ] \tag{27} ⎣⎢⎢⎢⎢⎡a1,1a2,1000a1,2a2,2a3,2000a2,3a3,3a4,3000a3,4a4,4a5,4000a4,5a5,5⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡T1T2T3T4T5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡Su,1Su,2Su,3Su,4Su,5⎦⎥⎥⎥⎥⎤(27)
然后代入数值,求解方程组,得
[ T 1 T 2 T 3 T 4 T 5 ] = [ 150 218 254 258 230 ] (28) \left [ \begin{matrix} T_1 \\ T_2 \\ T_3 \\ T_4 \\ T_5 \end{matrix} \right ]= \left [ \begin{matrix} 150\\ 218\\ 254\\ 258\\ 230 \end{matrix} \right ] \tag{28} ⎣⎢⎢⎢⎢⎡T1T2T3T4T5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡150218254258230⎦⎥⎥⎥⎥⎤(28)
该问题的解析解是
T = [ T B − T A L + q 2 k ( L − x ) ] x + T A (29) T=\left[ \frac{T_B -T_A}{L} + \frac{q}{2k}(L-x) \right]x +T_A \tag{29} T=[LTB−TA+2kq(L−x)]x+TA(29)
数值解与解析解的对比,
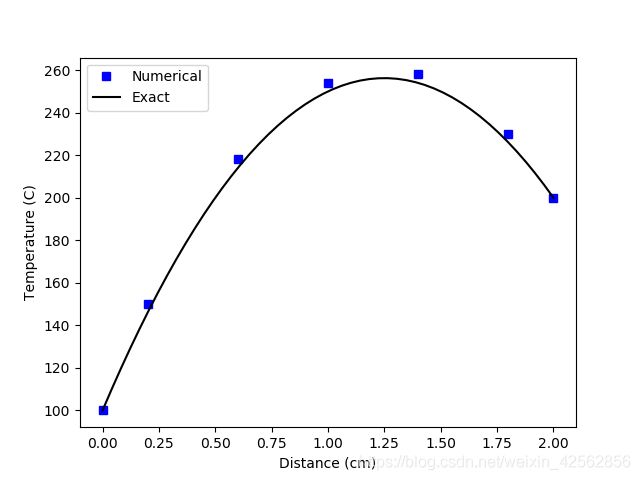
误差有点儿大,细化网格,将计算域划分为10个网格单元,则
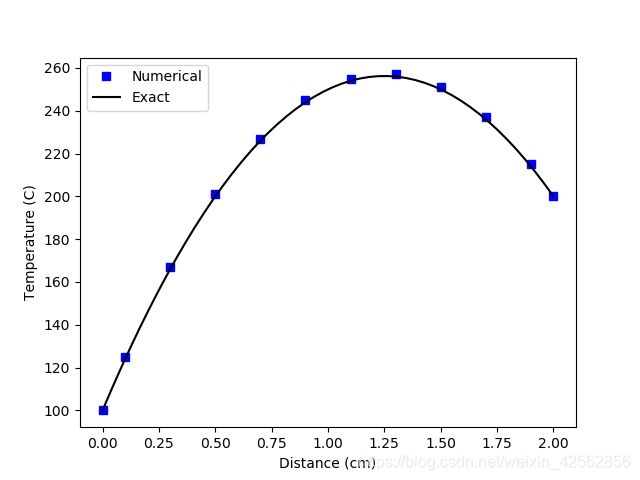
划分为20个网格单元,
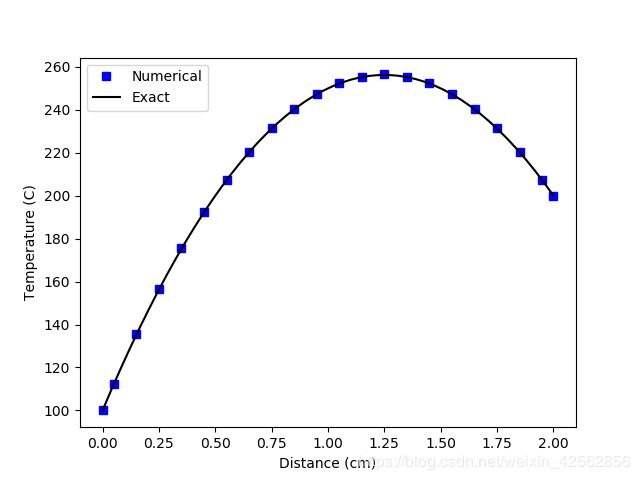
可见,细化网格可以提高计算精度,缩小数值解与解析解之间的误差。
计算程序
import numpy as np
import matplotlib.pyplot as plt
#== parameters ===
nx = 5 # 网格单元数
nndoes = nx + 2 # 节点数,含边界
#=== for example 1 ==========
'''
L = 0.5 # 长度,m
Area = 0.01 #截面面积 ,m2
k = 1000 #导热系数 , W/m-k
Ta = 100 # 边界A的温度值 ,C
Tb = 500 # 边界B的温度值 ,C
q = 0 # kW/m3, 体积热源
'''
# =========================
#***** for example 2 *********
#'''
L = 0.02 # 长度,m
Area = 1 #截面面积 ,m2
k = 0.5 #导热系数 , W/m-k
Ta = 100 # 边界A的温度值 ,C
Tb = 200 # 边界B的温度值 ,C
q = 1e6 # W/m3, 体积热源
#'''
#****************************
#== x grid ==
dx = L/nx # 网格间距
print('dx = ',dx)
x = np.zeros(nndoes) # x网格
x[1:nndoes-1] = np.linspace(dx/2, L-dx/2, nx) # 以边界A为原点创建网格点的坐标值
x[-1] = x[-2] + dx/2 #边界B的坐标值
print('x grid = ', x, '\n')
#== solution array ==
tt = np.zeros(nndoes) # 解向量
tt[0] = Ta # 边界值
tt[-1] = Tb
#== matrix ==
A = np.zeros((nx, nx))
b = np.zeros(nx)
su = q*dx
for i in range(1, nx-1): # 内部网格节点
A[i][i-1] = -k*Area/dx
A[i][i+1] = -k*Area/dx
A[i][i] = -(A[i][i-1] + A[i][i+1])
b[i] = su
# for boundary A
i = 0
A[i][i+1] = -k*Area/dx
su = 2*k*Area*Ta/dx + q*dx
sp = -2*k*Area/dx
A[i][i] = -A[i][i+1] - sp
b[i] = su
# for boundary B
i = nx-1
A[i][i-1] = -k*Area/dx
su = 2*k*Area*Tb/dx + q*dx
sp = -2*k*Area/dx
A[i][i] = -A[i][i-1] - sp
b[i] = su
print('A = \n', A, '\n')
print('b = \n', np.matrix(b).T ,'\n')
t_temp = np.linalg.solve(A, b)
print('solution = \n', np.matrix(t_temp).T, '\n')
tt[1:nndoes-1] = t_temp
xx = np.linspace(0, L, 50, endpoint=True)
exact_tt = np.zeros(50)
for i in range(50):
#exact_tt[i] = 800*xx[i] + 100 # 例1 解析解
exact_tt[i] = ((Tb-Ta)/L + q*(L-xx[i])/(2*k)) * xx[i] + Ta # 例2 解析解
plt.xlabel('Distance (cm)')
plt.ylabel('Temperature (C)')
plt.plot(x*100,tt ,'bs', label='Numerical')
plt.plot(xx*100,exact_tt,'k', label='Exact')
plt.legend()
plt.show()
参考资料
- Versteeg H K , Malalasekera W . An introduction to computational fluid dynamics : the finite volume method = 计算流体动力学导论[M]. 世界图书出版公司, 2010.