SPH算法简介（二）: 粒子受力分析

【原文链接：https://thecodeway.com/blog/?p=139】

        SPH算法的基本设想，就是将连续的流体想象成一个个相互作用的微粒，这些例子相互影响，共同形成了复杂的流体运动，对于每个单独的流体微粒，依旧遵循最基本的牛顿第二定律。

	(2.1)

        SPH这是我们分析的基础，在SPH算法里，流体的质量是由流体单元的密度决定的，所以一般用密度代替质量

	(2.2)

        这里的的作用力F的量纲发生变化，dim F=MT^-2L^-2，后面的分析都是用这个量纲的“作用力”，这一点一定要注意。作用在一个微粒上的作用力由三部分组成

	(2.3)

        其中F^External称为外部力，一般就是重力，所以

	(2.4)

        F^Pressure是由流体内部的压力差产生的作用力，试想一下在水管中流动的液体，进水口区域的压力一定会比出水口区域大，所以液体才会源源不断的流动，数值上，它等于压力场的梯度，方向由压力高的区域指向压力低的区域。

	(2.5)

        F^Viscosity是由粒子之间的速度差引起的，设想在流动的液体内部，快速流动的部分会施加类似于剪切力的作用力到速度慢的部分，这个力的大小跟流体的粘度系数μ以及速度差有关

	(2.6)

        带入公式2.2，可以得到

	(2.7)

        加速度形式：

	(2.8)

        如果你学习过流体力学，一定会发现上面这个公式就是Navier-Stokes方程的一个简单形式，但N-S方程有更严格的形式和推导过程，感兴趣的朋友可以从流体力学相关的书中找到，这里有一篇比较比较浅显的文档可以参考，经过联系作者flysea，拿到这篇文档的原始文件放在这里，再次感谢flysea的帮助。
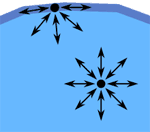
        实际运算过程中，有时还要考虑表面张力的影响，所谓表面张力大家应该并不陌生，肥皂泡、毛细管等有趣的物理现象都跟表面张力有关，这个力可以简单理解为流体试图减小表面而产生的力。

表面张力是由于界面层流体分子受力不均衡产生的

        由于表面张力只涉及到表层的粒子，所以计算方法和上面的有所不同，这部分会在以后的章节介绍。
        经过上面的分析，我们基本上搞清楚了SPH粒子的运动计算方法，下节我们将正式开始介绍SPH算法的关键部分，如何通过光滑核函数计算粒子运动规律。