回文树介绍(Palindromic Tree)

简介

回文树是由Mikhail Rubinchik大神发明的，在Petrozavodsk Summer Camp 2014上首次提出来，是一个很新的数据结构，目前相关资料比较少。

顾名思义，回文树是一个用来解决回文串相关问题的数据结构。

回文树的结构

就像线段树、平衡树等其它树结构一样，回文树由若干个节点组成，每个节点代表一个回文串(palindrome)。

节点

例子：四个节点的回文串

边

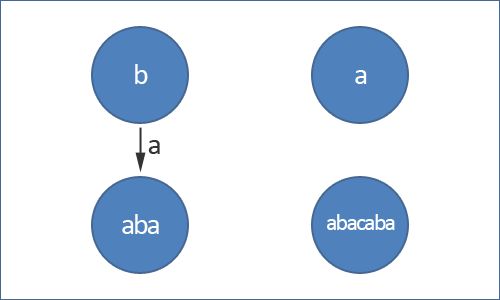
节点之间通过有向边连接起来，回文树中有两种类型的边，第一种类型的边上同时有字符做标记，比如： u 和 v 通过带字符 X 的边连接起来，表示节点 u 所表示的回文串两边添加 X 字符可以得到 v 节点所表示的回文串。以下是一个例子：

边：在 b 的两侧分别添加字符 a 得到新的回文串 aba

回文树中另一种类型的边是后缀链接边(suffix link)。从 u 到 w 存在一条后缀链接边，当且仅当 w 节点所代表的回文串是 u 的后缀中最长的回文串，但 w 和 u 不能相同（后缀：包含最后一个字符的子串， bcd 是 abcd 的后缀，但 bc 不是 abcd 的后缀）。

下面是一个例子：

后缀链接：虚线表示从 aba 到 a 的后缀链接边，因为 a 是 aba 最长的后缀回文串

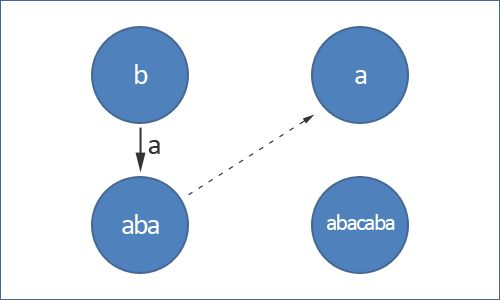
“回文树”这个名字可能会让人产生疑惑，因为回文树这个数据结构并不是一棵普通的树，它有两个根，一个根表示长度为-1的回文串，是我们为了方便操作加进去的，长度为1的回文串可以通过它左右两侧各添加一个字符得到。另一个根表示长度为0的回文串，即空串。

注意，我们并不在每个节点中实际存储它所表示的回文串，否则很容易爆内存，节点中仅仅包含如下信息：1.回文串长度；2.通过所有字符连接的边（即第一种类型的边）；3.后缀链接边（即第二种类型的边）。还有其它根据实际问题需要添加的边。

回文树的构造

对于一个给定的字符串 s ，它所对应的回文树就包含了 s 所有的回文子串，由于一个长度为n的字符串最多只有n个本质不同的回文子串（可以尝试自己证明这个结论，并不难，提示：考虑新加一个字符最多会贡献多少个新的回文子串），因此回文树的节点数目不会超过字符串的长度 + 2，另外两个是前面提到的两个虚拟的根。

从空串开始，每次添加一个字符，并更新回文树。假设我们已经处理了字符串的某个前缀 p ，接下来要添加的字符是 x 。

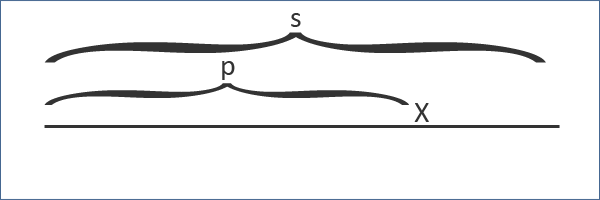
同时需要维护前缀 p 的最长后缀回文串，不妨设为 t 。

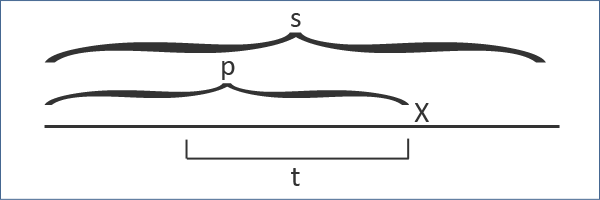
由于 t 已经处于某个已经处理的前缀中，因此它必定对应于回文树上的某个节点，这个节点会有后缀链接边指向其他节点，然后这个节点再指向其他节点，形成一个链。下面是的图示：

从 t 出发的后缀链接

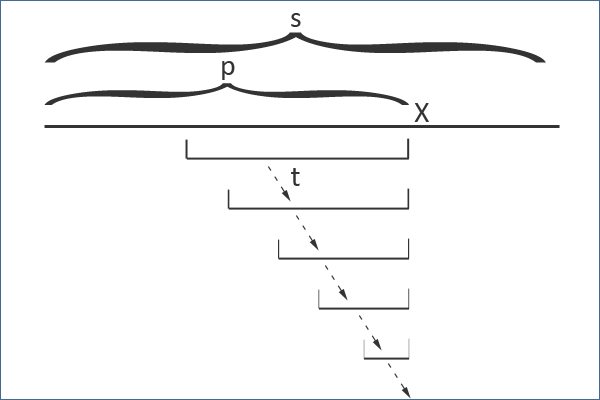
现在我们来找新前缀 p+x 的后缀回文串，这个回文串肯定是 xAx 的形式，其中 A 是某个回文串（注意 A 可能为空，或者对应于长度为-1的根，此时的后缀回文串就是 x 这一个字符啦）。同时注意到， A 是 p 的后缀，因此一定可以从 t 出发通过后缀链接边到达 A 所对应的节点。

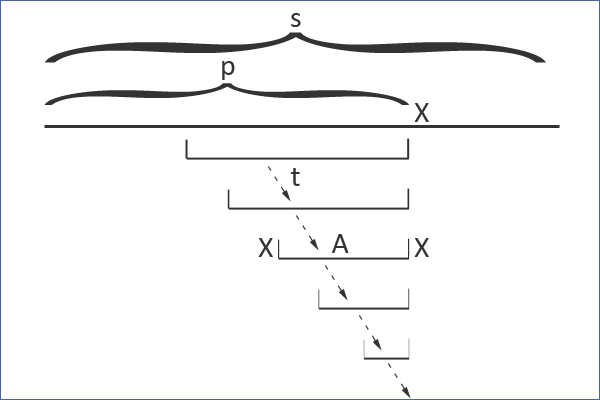
字符串 xAx 是唯一一个有可能在 p+x 中出现却从来没有在前缀 p 中出现的回文串。原因也很简单，因为所有可能的新回文串都必须以 x 为结尾，因此必定是 p+x 的后缀回文串。由于 xAx 是 p+x 的最长后缀回文串，因此其它更短的回文串必定是在 xAx 的前缀中出现了，也就是在前缀 p 中出现过。证毕。

所以，为了处理这个新添加的字符 x ，我们需要沿着后缀链接边走，直到找到一个合适的 A (也有可能一直回溯到根)。然后我们检查与 A 相对应的节点是否与一条标记为 x 的边，如果没有的话，就添加一条边指向新的节点 xAx 。(有的话就什么都不用做了。。)

接下来还需要更新 xAx 的后缀链接边，如果后缀链接边已经存在，那就不需要做任何事情了。否则，我们就找到 xAx 的最长后缀回文串，必定是有 xBx 的形式，其中 B 有可能是空串。按照前面的逻辑， B 是前缀 p 的后缀回文串并且从 t 通过边可达。

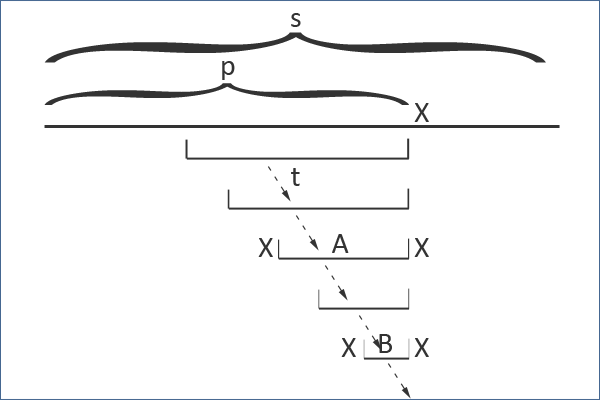
总结一下回文树的构造过程。从左到右一个字符一个字符地处理，始终维护着当前已处理前缀的最长后缀回文串(初始时为空串)。每次扫描一个新的字符 x 是，我们就沿着后缀链接边找到一个回文串 A ，它的两边可以同时添加字符 x ，得到一个合法的后缀回文串。 xAx 是新节点的唯一候选，为了得到它的后缀链接边，我们需要继续沿着链接走，直到找到另一个回文串 B ，它的两边添加字符 x 可以得到 xAx 的合法后缀回文串，于是添加一条从 xAx 到 xBx 的边（当然，如果这条边已经存在就不用了）。

为了更好地理解，可以看看下面的代码，其中变量num忽略掉就行了，它是为了计数回文子串个数的。

#include 
using namespace std;

const int MAXN = 1005;

struct node {
    int next[26];
    int len;
    int sufflink;
    int num;
};

int len;
char s[MAXN];
node tree[MAXN];
int num;            // node 1 - root with len -1, node 2 - root with len 0
int suff;           // max suffix palindrome
long long ans;

bool addLetter(int pos) {
    int cur = suff, curlen = 0;
    int let = s[pos] - 'a';

    while (true) {
        curlen = tree[cur].len;
        if (pos - 1 - curlen >= 0 && s[pos - 1 - curlen] == s[pos])
            break;
        cur = tree[cur].sufflink;
    }
    if (tree[cur].next[let]) {
        suff = tree[cur].next[let];
        return false;
    }

    num++;
    suff = num;
    tree[num].len = tree[cur].len + 2;
    tree[cur].next[let] = num;

    if (tree[num].len == 1) {
        tree[num].sufflink = 2;
        tree[num].num = 1;
        return true;
    }

    while (true) {
        cur = tree[cur].sufflink;
        curlen = tree[cur].len;
        if (pos - 1 - curlen >= 0 && s[pos - 1 - curlen] == s[pos]) {
            tree[num].sufflink = tree[cur].next[let];
            break;
        }
    }
    tree[num].num = 1 + tree[tree[num].sufflink].num;
    return true;
}

void initTree() {
    num = 2; suff = 2;
    tree[1].len = -1; tree[1].sufflink = 1;
    tree[2].len = 0; tree[2].sufflink = 1;
}

int main() {
    scanf("%s", s);
    len = strlen(s);

    initTree();

    for (int i = 0; i < len; i++) {
        addLetter(i);
        ans += tree[suff].num;
    }
    cout << ans << endl;
    return 0;
}

以上代码可以直接提交通过SPOJ NUMOFPAL。可以看到，虽然解释了一大堆，但其实代码写起来还挺短的。

时间复杂度

注意到，在从左到右扫描字符串的过程中，最长后缀回文串的左边界只可能向右移动，并且最多移动 n 次，与后缀链接边相对应的左边界也只可能向右移动，并且最多移动 n 词。因此总的时间复杂度是 O(|S|) 或者说 O(N) 的。

空间复杂度

空间复杂度为 O(|alphbet|∗N) ，还有其他几个数组，可以忽略掉。对于小写英文字母表 |alphabet|=26 。

应用

末尾追加一个字符，会产生多少个新的回文串？

举个例子，如果我们在字符串 aba 后面添加一个新的字符 a ，已经存在的回文串有 a , b , aba ，新产生的回文串为 aa 。根据前面的讨论，这个问题的答案只可能是0或者1，当我们更新回文树的时候，插入这个新的字符，如果新产生了新节点，那么答案就是1，否则就是0。

回文子串的数目

给定一个字符串，计数这个字符串当中有多少个回文子串。比如， aba 有四个：两个 a ,一个 b ，一个 aba 。这个问题其实就是上面的代码所解决的问题，当我们扫描到一个新字符的时候，将结果累加上以这个字符结尾的后缀回文字符串个数，这个数字就是新节点通过后缀链接边可达的节点个数，为了高效计数，可以在每个节点新增一个域num，表示由该节点出发的链接长度。对于根节点而言，链长为0，对于其他节点，链长为其后续节点的链长 + 1.

这个问题还可以用Manacher’s algorithm求解，时间复杂度也是 O(N) 。但回文树相对更好写并且应用的范围更广。

回文串出现的个数统计

这个问题要求统计出每个回文串各出现了多少次，解决的思路和上面类似，每扫描一个新的字符 x 时，就对新出现的最长后缀回文串以及它可达的所有回文串计数加1。为了加快更新速度，需要类似于线段树那样采用一个延迟更新的策略，就不多说了。。

最后再进行一遍计数值的传播更新，就可以得到所有回文串出现的次数了。

结论

本文介绍了一个新的数据结构——回文树，可以膜拜这个代码。其实，回文树的基本想法跟KMP算法、AC自动机是比较相似的，都是在匹配失败的时候找到最优的后缀之类的。。

同时根据poursoul大神的推荐，可以刷刷下面几道题：

1.ural1960. Palindromes and Super Abilities
2.TsinsenA1280. 最长双回文串
3.TsinsenA1255. 拉拉队排练
4.TsinsenA1393. Palisection
5.2014-2015 ACM-ICPC, Asia Xian G The Problem to Slow Down You
6.Trie in Tina Town

有建议或者发现错误，欢迎交流。

原文的地址：http://adilet.org/blog/25-09-14/