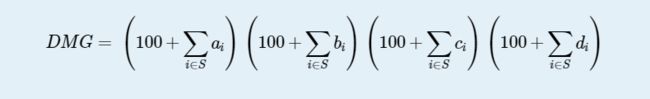2020杭电多校第二场(解题报告)
1001-Total Eclipse
题意:有个n个点m条边的图,每个点都有权值,每次可以选择一个点权全是正数的连通块,让他们的权值整体-1,问把所有点权值变成0需要多少次操作。(1≤n,m≤1e5)
样例输入:
1
3 2
3 2 3
1 2
2 3输出:
4hint:并查集。
正难则反。反着操作,先按照权值从大到小排序,从最大点开始倒着添加边,一开始加入新的点,作为单独的个体i,需要操作ai次,然后把他相邻的边依次加上。当他的存在使得两个连通块融合时,那么两个连通块共享这个i,并且两个连通块上所有点权值都大于i,因此省去了ai次操作,答案-ai。
AC代码:
#include
using namespace std;
const int N = 123456;
int pre[N],vis[N];
struct node{
int val,id;
bool operator < (const node &a){
return val>a.val;
}
}a[N];
vectorv[N];
int find(int a){
if(a==pre[a])return a;
return pre[a]=find(pre[a]);
}
int main(){
int t;scanf("%d",&t);
while(t--){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
pre[i]=i;
vis[i]=0;
v[i].clear();
int x;scanf("%d",&x);
a[i]={x,i};
}
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
v[x].push_back(y);
v[y].push_back(x);
}
sort(a+1,a+n+1);
long long sum=0;
for(int i=1;i<=n;i++){
sum+=a[i].val;
int id=a[i].id;
for(auto j:v[id]){
if(!vis[j])continue;
int u=find(id),v=find(j);
if(u!=v){
pre[u]=v;
sum-=a[i].val;
}
}
vis[id]=1;
}
printf("%lld\n",sum);
}
system("pause");
return 0;
} 1006-The Oculus
题意:f[i]是斐波那契数列,f[1]=1,f[2]=2,f[3]=3,f[4]=5
BB:{b1,b2,b3,,,bi}其中bi={0,1},每个数都可以用某些斐波那契数相加得到,比如4={1,0,1}=1*1+0*1+1*3
给出ABC的BB表示,问是否有一个fk使得A*B=C+fk。范围如下:
输入:
1
3 1 0 1
4 0 0 0 1
6 0 1 0 0 0 1输出:
4hint:unsigned long long的自然溢出可以实现,直接暴力跑 ,不过注意开数组范围要超过2e6。
#include
using namespace std;
const int N = 2345678;
#define ull unsigned long long
ull f[N];
ull inline read(){
ull ans=0;
int n;scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
if(x)ans+=f[i];
}
return ans;
}
int main(){
f[1]=1;f[2]=2;
for(int i=3;i<=N;i++)f[i]=f[i-1]+f[i-2];
int t;scanf("%d",&t);
while(t--){
ull a,b,c;
a=read();
b=read();
c=read();
a*=b;
int i=1;
while(c+f[i]!=a)i++;
printf("%d\n",i);
}
system("pause");
return 0;
} 1010-Lead of Wisdom
题意:有n个装备,不超过k种,每种装备都有它的属性值ai,bi,ci,di,让你取出不同种类的各一种,使得以下式子的值最大
输入:
1
6 4
1 17 25 10 0
2 0 0 25 14
4 17 0 21 0
1 5 22 0 10
2 0 16 20 0
4 37 0 0 0输出:
297882000hint:优化版的暴搜(添加了个nxt数组,可以少跑好几层递归)
AC代码:
#include
using namespace std;
#define LL long long
struct node{
int a,b,c,d;
}tmp;
vectorv[55];
LL ans=0;
int n,k;
int nxt[55];
void dfs(int x,int a,int b,int c,int d){
if(x>k){
ans=max(ans,1LL*a*b*c*d);
return;
}
if(v[x].size()==0){
dfs(nxt[x],a,b,c,d);
return;
}
for(auto i:v[x]){
dfs(x+1,a+i.a,b+i.b,c+i.c,d+i.d);
}
}
int main(){
int t;scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&k);
for(int i=1;i<=k;i++)v[i].clear();
for(int i=1;i<=n;i++){
int op,a,b,c,d;
scanf("%d%d%d%d%d",&op,&a,&b,&c,&d);
tmp={a,b,c,d};
v[op].push_back(tmp);
}
int x=k+1;
for(int i=k;i;i--){
nxt[i]=x;
if(v[i].size())x=i;
}
ans=0;
dfs(1,100,100,100,100);
printf("%lld\n",ans);
}
system("pause");
return 0;
} 1012-String Distance
题意: 给字符串a,b,q次查询,求a[l...r]与b的最长公共子串
输入:
1
qaqaqwqaqaq
qaqwqaq
3
1 7
2 8
3 9输出:
4
2
0hint:序列自动机+DP求LCS
nxt[i][j]表示a[i...n]种第一个出现字母j的位置
dp[i][j]表示b的前i个字母匹配了j个了,最后一个匹配的字母在a中的位置
#include
using namespace std;
const int N = 123456;
int nxt[N][50];//a[i...n]中字母j的最近位置
int dp[50][50];//b中前i个字母匹配了j个,dp[i][j]表示最后一个匹配的字母在a中的位置
char a[N],b[N];
void get_nxt(){//序列自动机
int lena=strlen(a+1);
for(int i=0;i<26;i++)nxt[lena][i]=lena+1;
nxt[lena][a[lena]-'a']=lena;
for(int i=lena-1;i>=1;i--){
for(int j=0;j<26;j++){
nxt[i][j]=nxt[i+1][j];
}
nxt[i][a[i]-'a']=i;
}
}
int main(){
int t;scanf("%d",&t);
while(t--){
scanf("%s%s",a+1,b+1);
int lenb=strlen(b+1);
get_nxt();
int q;scanf("%d",&q);
while(q--){
int l,r;
scanf("%d%d",&l,&r);
memset(dp,0x3f3f3f3f,sizeof(dp));
dp[0][0]=l-1;
for(int i=1;i<=lenb;i++){
dp[i][0]=l-1;
for(int j=1;j<=i;j++){
if(dp[i-1][j]<=r)dp[i][j]=min(dp[i][j],dp[i-1][j]);//b[j]不匹配
if(dp[i-1][j-1]