全排列算法整理
全排列算法整理
本文整理了全排列算法的:
- 递归实现
- 含重复元素的递归实现
- 深搜实现(字典序)
- 含重复元素的深搜实现(字典序)
- 非递归字典序实现——下一个排列(可含重复元素)
递归实现
我们接触的第一个全排列算法大多都是这个递归的算法。参考了王晓东的《计算机算法设计与分析第三版》:
设 R={r1,r2,...,rn} R = { r 1 , r 2 , . . . , r n } 是要进行排列的 n n 个元素, Ri=R−{ri} R i = R − { r i } 。集合 X X 中元素的全排列记为 Perm(X) P e r m ( X ) 。 (ri)Perm(X) ( r i ) P e r m ( X ) 表示在全排列 Perm(X) P e r m ( X ) 的每一个排列钱加上前缀 ri r i 得到的排列。 R R 的全排列可归纳定义如下:
当 n=1 n = 1 时, Perm(R)=(r) P e r m ( R ) = ( r ) ,其中 r r 是集合 R R 中唯一的元素;
当 n>1 n > 1 时, Perm(R) P e r m ( R ) 由 (r1)Perm(R1),(r2)Perm(R2),...,(rn)Perm(Rn) ( r 1 ) P e r m ( R 1 ) , ( r 2 ) P e r m ( R 2 ) , . . . , ( r n ) P e r m ( R n ) 构成。
依次递归定义,可设计产生 Perm(R) P e r m ( R ) 的递归算法代码如下:
#include 算法 Perm(list,k,m) P e r m ( l i s t , k , m ) 递归地产生所有前缀是 list[0:k−1] l i s t [ 0 : k − 1 ] ,且后缀是 list[k:m] l i s t [ k : m ] 的全排列的所有排列。函数调用 Perm(list,0,n−1) P e r m ( l i s t , 0 , n − 1 ) 则产生 list[0:n−1] l i s t [ 0 : n − 1 ] 的全排列。
在一般情况下, k<m k < m 。算法将 list[k:m] l i s t [ k : m ] 中的每一个元素分别与 list[k] l i s t [ k ] 中的元素交换。然后递归的计算 list[k+1:m] l i s t [ k + 1 : m ] 的全排列,并将计算结果作为 list[0:k] l i s t [ 0 : k ] 的后缀。算法中Swap是用于交换两个变量值的内联函数。
含重复元素的递归实现
从上面可以看出全排列的第一个元素 需要依次和它后面的元素进行交换,当后面的元素中有重复元素时,比如:
数字122,第一个数字1和第二个数字2交换,可以得到2 12,这将生成以2为前缀,以12的全排列为后缀的所有排列。
第一个数字1与第三个数字2交换,可以得到2 21, 这将生成以2为前缀,以21的全排列为后缀的所有排列。
而12和21的全排列是相同的,所以上述两种交换得到的排列一定是重复的。
去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。
即第i个数与第j个数交换时,要求[i,j)中没有与第j个数相等的数。
#include 深搜实现
深搜也可以实现全排列,用一个visit[]数组记录当前那些元素已经被选,继续搜索没有被选的元素。
1. 数的全排列
给定数字n,输出数字1~n的全排列。比如给定数字3,输出:1 2 3 ,1 3 2 ,2 1 3 ,2 3 1 ,3 1 2 ,3 2 1
代码:
#include 2.字符的全排列
上面的数的全排列稍微改动一下就是字符的全排列。我们可以生成数字0~n-1的全排列,这个数的全排列即字符数组的下标的全排列。输出的时候按下标输出字符即可。visit[]记录的还是下标。
代码:
#include 也可以用一个256个元素的visit[]数组记录当前元素是否被选中过,而不是记录当前的下标。
/*
* 通过记录元素的不含重复元素的字符的全排列
*/
void dfs_ch1(int step) {
if(step == len) {
for(int i = 0; i < len; i++) {
cout << perm_ch[i] << " ";
}
cout << endl;
}
else {
for(int i = 0; i < len; i++) {
if(!visit[(int)s[i]]) {
perm_ch[step] = s[i];//perm_ch[]是一个char数组,用于记录排列
visit[(int)s[i]] = 1;
dfs_ch1(step+1);
visit[(int)s[i]] = 0;
}
}
}
}含重复元素的深搜实现
上面第二种字符的全排列方式要求字符串s[]中不允许出现重复元素,否则该算法将无法满足终止条件。
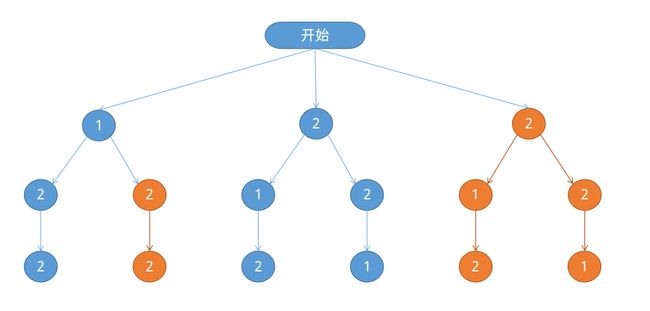
如果用上面第一种算法,按照下标的全排列来生成字符串122的全排列,全排列的解答树如下:
我们注意到橘黄色的树显示的都是已经出现过的排列,即我们需要剪掉的树枝。
我们希望在搜索子树的时候,不要出现重复的子树,否则一定会出现重复的排列。
如上图的第一层的第三棵子树,其根节点为2,与第二棵子树的根节点相同,又由于第二棵子树和第三棵拥有同样的祖先,所以在这两个子树下搜索时visit[]数组是完全相同的,所以这两个子树也必定完全相同。
所以,在第一层的搜索中,当发现第三个节点与前面已经出现过的一个节点相同时(即第二个节点),就不该继续搜索此树,应将其剪掉。
如果字符串s[]已经有序,则每次搜索新的子树的时候,只需要判断当前搜索到的子树的根节点是否与上一个搜索到的子树的根节点相同。用一个变量pre记录上一个搜索过的节点的下标,如果当前搜索的节点s[i]==s[pre],则跳过该次搜索,即剪掉这棵子树。
代码:
/*
* 通过记录下标实现的含重复元素的全排列
*/
void dfs_ch2(int step)
{
if(step == len) {
for(int i = 0; i < len; i++) {
cout << s[perm[i]] << " ";
}
cout << endl;
}
else {
int pre = 0;//记录前一个选中的根节点
for(int i = 0; i < len; i++) {
if(!i || s[pre] != s[i]) { //与前一个选中的子树的根节点不重复
if(!visit[i]) {
perm[step] = i;
visit[i] = 1;
dfs_ch2(step+1);
visit[i] = 0;
pre = i;//记录pre
}
}
}
}
}如果用visit[]记录元素的方式, 我们可以用一个count[]数组记录每个元素出现的次数,表明该元素可以在全排列中选中的次数,将原本的 if(!visit[(int)s[i]])可以改为if(visit[(int)s[i]] < count[(int)s[i]])。
如果字符串s[]已经有序,则每次只需要搜索s[]的第一个元素和“与前一个元素不相同”的元素。即每次搜索子树的时候,在 for(int i = 0; i < len; i++) 和起后的大括号之前加上if(!i || s[i] != s[i-1])。这样就保证了重复元素绝对不会出现在同一层(s[]已经有序的情况下)。在 for(int i = 0; i < len; i++) 和起后的大括号之前加上if(!i || s[i] != s[i-1]),问题就解决了。
代码:
/*
* 通过记录元素出现个数实现的含重复元素的全排列
*/
void dfs_ch3(int step) {
if(step == len) {
for(int i = 0; i < len; i++) {
cout << perm_ch[i] << " ";
}
cout << endl;
}
else {
for(int i = 0; i < len; i++) {
if(!i || s[i] != s[i-1]) {
if(visit[(int)s[i]] < count[(int)s[i]]) {
perm_ch[step] = s[i];
visit[(int)s[i]]++;
dfs_ch3(step+1);
visit[(int)s[i]]--;
}
}
}
}
} 非递归字典序实现
非递归的全排列即不断地求当前字符串在字典序下的“下一个排列”。如”1234”的下一个排列就是”1243”,“1243”的下一个排列是“1324” …… 直到求得“4321”,找不到比当前排列字典序更大的排列,算法终止。
如何计算字符串的下一个排列了?来考虑”926520”这个字符串,我们从后向前找第一双相邻的递增数字,”20”、”52”都是非递增的,”26 “即满足要求,称前一个数字2为替换数,替换数的下标称为替换点,再从后面找一个比替换数大的最小数(这个数必然存在),0、2都不行,5可以,将5和2交换得到”956220”,然后再将替换点后的字符串”6220”颠倒即得到”950226”。
对于像”4321”这种已经是最“大”的排列,采用STL中的处理方法,将字符串整个颠倒得到最“小”的排列”1234”并返回false。
用更严谨一点的描述:
设P是1~n的一个全排列: p=p1p2......pn=p1p2......pj−1pjpj+1......pk−1pkpk+1......pn p = p 1 p 2 . . . . . . p n = p 1 p 2 . . . . . . p j − 1 p j p j + 1 . . . . . . p k − 1 p k p k + 1 . . . . . . p n
1. 从排列的右端开始,找出第一个比右边数字小的数字的序号j(j从左端开始计算), j=max{i|pi<pi+1} j = m a x { i | p i < p i + 1 }
2. 在 pj p j 的右边的数字中,找出所有比pj大的数中最小的数字pk,即 k=maxi|pi>pj k = m a x i | p i > p j (右边的数从右至左是递增的,因此k是所有大于 pj p j 的数字中序号最大者)
3. 对换pi,pk
4. 再将 pj+1......pk−1pkpk+1......pn p j + 1 . . . . . . p k − 1 p k p k + 1 . . . . . . p n 倒转得到排列 p′=p1p2.....pj−1pjpn.....pk+1pkpk−1.....pj+1 p ′ = p 1 p 2 . . . . . p j − 1 p j p n . . . . . p k + 1 p k p k − 1 . . . . . p j + 1 ,这就是排列p的下一个排列。
关于这个next_permutation算法的证明,参考:http://blog.csdn.net/lohiaufung/article/details/52901564
还有:http://blog.fly2best.com/algo/2013/06/21/next_permutation/
代码:
#include 本文参考了:
1. http://blog.csdn.net/morewindows/article/details/7370155/
2. http://blog.csdn.net/cpfeed/article/details/7376132
3. http://blog.csdn.net/lohiaufung/article/details/52901564
4. http://blog.fly2best.com/algo/2013/06/21/next_permutation/