- Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
- 《 C++ 修炼全景指南:九 》打破编程瓶颈!掌握二叉搜索树的高效实现与技巧
Lenyiin
C++修炼全景指南技术指南c++算法stl
摘要本文详细探讨了二叉搜索树(BinarySearchTree,BST)的核心概念和技术细节,包括插入、查找、删除、遍历等基本操作,并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度,同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类,读者能够掌握其实际应用,此外,文章还建议进一步扩展为平衡树(如AVL树、红黑树)以优化极端情况下的性能退化。
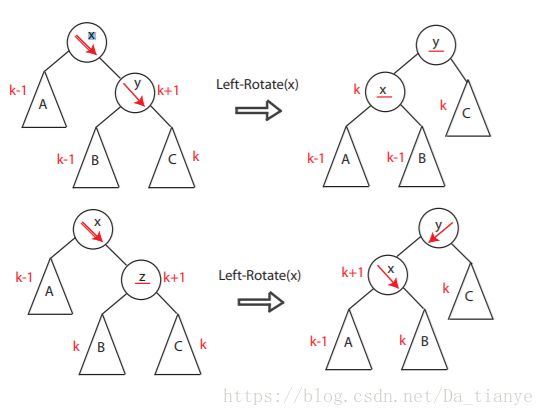
- 《 C++ 修炼全景指南:十 》自平衡的艺术:深入了解 AVL 树的核心原理与实现
Lenyiin
C++修炼全景指南技术指南c++数据结构stl
摘要本文深入探讨了AVL树(自平衡二叉搜索树)的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理,并详细分析了其四种旋转操作,包括左旋、右旋、左右双旋和右左双旋,阐述了它们在保持树平衡中的重要作用。接着,本文从头到尾详细描述了AVL树的插入、删除和查找操作,配合完整的代码实现和详尽的注释,使读者能够全面理解这些操作的执行过程。此外,我们还提供了AVL树的遍历方法,包括中序、前序和后序遍历,
- leetcode中等.数组(21-40)python
九日火
pythonleetcode
80.RemoveDuplicatesfromSortedArrayII(m-21)Givenasortedarraynums,removetheduplicatesin-placesuchthatduplicatesappearedatmosttwiceandreturnthenewlength.Donotallocateextraspaceforanotherarray,youmustdoth
- LeetCode 673. Number of Longest Increasing Subsequence (Java版; Meidum)
littlehaes
字符串动态规划算法leetcode数据结构
welcometomyblogLeetCode673.NumberofLongestIncreasingSubsequence(Java版;Meidum)题目描述Givenanunsortedarrayofintegers,findthenumberoflongestincreasingsubsequence.Example1:Input:[1,3,5,4,7]Output:2Explanatio
- 2021-08-24 Say no to the next social
春生阁
Youknowthesort.Drinkswitholdfriendsyouhavenothingincommonwithanymore.Yoursecondcousinonceremoved’sbabyshowerwitha$100minimumpresentspend.Thesesortsofsocialengagementssuckthelivingtimeandmoneyoutofyou.
- linux的安装程序 与 文件 相关的命令
可能只会写BUG
c语言c/c++linuxlinux服务器运维
软件安装卸载命令软件包介绍软件包命名格式dpkg命令apt-get命令apt-get命令压缩和解压命令压缩文件后缀压缩命令打包和解包命令tar命令文件分割命令split命令文件操作相关命令cat命令head命令tail命令more命令less命令管道命令wc命令grep命令find命令cut命令sort命令uniq命令diff命令文件属性命令chmod命令chown命令chgrp命令ln命令硬链接
- B3798 梦熊培养计划
summ1ts
算法数据结构
排序:sort()函数方法1:sort(起始地址,末尾地址+1);方法2:sort(起始地址,末尾地址+1,cmp);//cmp是自定义的排序规则sort是默认升序排序的,如果需要自定义排序,可以写一个比较函数,用第二种方法排序。例如:对一个数组a进行升序排列,(a中的元素存储从a[1]~a[n]),则可以写成:sort(a+1,a+1+n);如果元素存储是:a[0]~a[n-1],则写成:sor
- C语言:冒泡排序的注意事项及具体实现
z_鑫
c语言算法数据结构开发语言
一、注意事项1、函数声明为:voidbubble_sort(void*base,size_tnum,size_twidth,int(*cmp)(constvoid*e1,constvoid*e2));2、base指向所要排序的数组3、num为数组的元素个数4、width为一个元素占多少个字节的空间5、cmp为函数指针,指向用来进行比较的函数6、每趟排序都会把当前未排序部分的最大值移到正确的位置二、
- 洛谷水题 记录
木木ainiks
算法c++数据结构
P1093[NOIP2007普及组]奖学金sort排序即可注意cmp的写法#include#includeusingnamespacestd;structnode{intid;intchinese;intmath;intenglish;intcount;}a[305];intcmp(node&a,node&b){if(a.count!=b.count){returna.count>b.count;
- 商业预测 初识R
hongyanwin
r语言预测
1.打开帮助文档首页,查阅其中的“IntroductiontoR”helpRhelp2.安装vcd包install.packages("vcd")3.列出此包中可用的函数和数据集ls("package:vcd")/data(package="vcd")4.载入包并阅读数据集Arthritis的描述library("v.d")/?Arthritis5.显示数据集Arthritis的内容查看数据集结构
- 压测服务器并使用 Grafana 进行可视化
豆瑞瑞
grafana
简介仓库代码GitCode-全球开发者的开源社区,开源代码托管平台参考Welcome!-TheApacheHTTPServerProjectGrafana|查询、可视化、警报观测平台https://prometheus.io/docs/introduction/overview/
- el-table实现多列排序
KOi..
vue.js前端javascript
业务需求el-table需要支持多列排序,后端排序。即就是在点击后重新发送请求,点击一列的排序,另一列的排序样式能够保留,但是el-table默认是单列排序。页面/***@header-click="handleHeaderCLick"*点击表头文字触发的监听器**@sort-change="handleTableSort"*点击表头排序标签触发定时器*/data:{tmpTotal:0,tabl
- JavaScript两个数组的交集 II
流落的小鬼
刷题记录:JavaScript两个数组的交集II给你两个整数数组nums1和nums2,请你以数组形式返回两数组的交集。输入:nums1=[1,2,2,1],nums2=[2,2]输出:[2,2]varintersect=function(nums1,nums2){varresult=[];vari=0,j=0;nums1.sort((a,b)=>a-b);nums2.sort((a,b)=>a-
- 方的ScalersTalk第四轮新概念朗读持续力训练Day203 20200301
daisy境界的彼方
练习材料:Weoftenreadinnovelshowaseeminglyrespectablepersonorfamilyhassometerriblesecretwhichhasbeenconcealedfromstrangersforyears.TheEnglishlanguagepossessesavividsayingtodescribethissortofsituation.Thete
- elementUI table排序 sortable
Artsman
前端开发技术elementui前端javascript前端框架
使用elementUI做后台程序时非常便利,但有时,插件的用法也会让人头疼。在列中设置sortable属性即可实现以该列为基准的排序,接受一个Boolean,默认为false。可以通过Table的default-sort属性设置默认的排序列和排序顺序。可以使用sort-method或者sort-by使用自定义的排序规则。如果需要后端排序,需将sortable设置为custom,同时在Table上监
- vue2 el-table指定某些数据不参与排序
前端~初学者
Vue2ElementUIvue.jsjavascriptecmascript
vue2el-table指定某些数据不参与排序1、需求描述2、配置属性方法3、详细代码如下1、需求描述最后一行总计不参与排序2、配置属性方法el-table需要配置@sort-change="soltHandle"方法el-table-column需要配置sortable="custom"属性3、详细代码如下{{getChineseName(row.province).value}}结算单meth
- windows C++-并行编程-并行算法(五) -选择排序算法
sului
windowsC++并行编程技术c++windows
并行模式库(PPL)提供了对数据集合并行地执行工作的算法。这些算法类似于C++标准库提供的算法。并行算法由并发运行时中的现有功能组成。在许多情况下,parallel_sort会提供速度和内存性能的最佳平衡。但是,当您增加数据集的大小、可用处理器的数量或比较函数的复杂性时,parallel_buffered_sort或parallel_radixsort性能更佳。确定在任何给定方案中使用哪种排序算法
- vue3-响应式API(工具函数)-unRef
hx_1199
vue3前端javascriptvue.js
unRef作用:如果参数是ref,则返回内部值,否则返回参数本身。理解:val=isRef(val)?val.value:val应用:sortField=unref(tableRef)?.getSortFields()
- JS 获取数组对象中某个属性的最大值或最小值
qq_36437172
JSMath.maxMath.minsortapply
最近的开发中经常会遇到前端自己生成唯一id,然后在数组中增加删除插入对象,这样一来就要的要当前使用的id的最大值。总结一下,有两种比较简便的方法可以做到:1.将属性值通过map生成一个数组,再使用Math.max取最大值2.使用排序sort,先对数组的项排序,再取排序后的对应的项的值数组对象如下,求id的最大值和最小值list=[{id:1,name:'jack'}, {id:2,name:
- 统计/nginx/access.log中每个ip的访问次数,按高到低排列
年薪丰厚
nginx运维
/nginx/access.log具体内容长这样:第一个元素就是ip。awk'{print$1}'/nginx/access.log|sort|uniq-c|sort-r首先,awk'{print$1}'/nginx/access.log从/nginx/access.log文件的每行中提取出第一个字段。然后,sort对提取出的第一个字段进行排序。接着,uniq-c统计每个唯一的字段出现的次数。最后
- 三点or多点的变换矩阵求解opencv & eigen
合工大机器人实验室
C++矩阵opencv线性代数
《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》,它使用SVD方法计算T和t。只要算出变换矩阵,就可以算出A坐标系的一个点P在坐标系B里的对应点坐标,即R为3x3的转换矩阵,t为3x1的位移变换向量,这里点坐标均为3x1的列向量(非齐次形式,齐次形式下为4x1列向量,多出的一个元素值补1而已)。理论上只
- VueTreeselect el-tree-select 多选
小小并不小
Vueelementjsvue.jsjavascript
1、VueTreeselect是一个多选组件npminstall--save@riophae/vue-treeselect全部代码//importthecomponentimportTreeselectfrom'@riophae/vue-treeselect'//importthestylesimport'@riophae/vue-treeselect/dist/vue-treeselect.cs
- KMP-看毛片算法
无休居士
数据结构
#include#includevoidinsert(int*arr,inta,intn){/*0到n-1都已排好序*/inti;intkey=a;for(i=0;i=i;j--){arr[j+1]=arr[j];}arr[i]=key;return;}}arr[n]=key;return;}voidsort(int*arr,intsize){if(size<2)return;inti;for(i
- antd of vue treeSelect——异步加载
who_become_gods
onLoadData(treeNode){varthat=thisreturnnewPromise((resolve)=>{if(treeNode.
- treeselect只选了分支节点全选_vue Treeselect 树形下拉框:获取选中节点的ids和lables操作...
weixin_39637285
API:https://vue-treeselect.js.org/#events1.ids:即value1.lable:需要用到方法:@select(node,instanceId)和@deselect(node,instanceId)v-model="DRHA_EFaultModeTree_value":multiple="true":options="DRHA_EFaultModeTree_
- 【ShuQiHere】快速排序(Quick Sort):揭开高效排序算法的神秘面纱
ShuQiHere
排序算法算法数据结构
【ShuQiHere】引言在计算机科学中,排序算法是我们日常编程不可或缺的一部分。无论是处理大量数据、优化搜索引擎,还是进行系统性能提升,排序算法都起到了至关重要的作用。在所有的排序算法中,快速排序(QuickSort)凭借其高效性和灵活的分治策略成为最受欢迎的排序算法之一。在这篇博客中,我们将深入探讨快速排序的原理、性能分析以及如何通过优化策略进一步提升其效率。1.什么是快速排序?(QuickS
- 【ShuQiHere】从插入排序到归并排序:探究经典排序算法的魅力与实战应用
ShuQiHere
排序算法算法
【ShuQiHere】引言在计算机科学领域,排序算法是我们日常编程中经常会遇到的基本问题。无论是对数据进行排序、查找,还是优化复杂系统,排序算法都起着至关重要的作用。在这篇文章中,我们将详细探讨两种经典排序算法:插入排序和归并排序,通过对它们的原理、时间复杂度和实际应用场景的分析,帮你更好地理解并灵活应用这些算法。1.插入排序:像整理扑克牌一样排序插入排序(InsertionSort)是一种简单且
- 【Leetcode】581. Shortest Unsorted Continuous Subarray
云端漫步_b5aa
Givenanintegerarray,youneedtofindonecontinuoussubarraythatifyouonlysortthissubarrayinascendingorder,thenthewholearraywillbesortedinascendingorder,too.Youneedtofindtheshortestsuchsubarrayandoutputitsle
- linux-L9.linux中对文件 按照时间排序 显示100 个
robot_大菜鸟
linux_dotilinuxjavascript运维
find.-typef-execstat--format'%Y%n'{}+|sort-nr|head-n100解释:•find.-typef:在当前目录下查找所有文件。•-execstat--format‘%Y%n’{}+:对每个找到的文件执行stat命令,以获取文件的修改时间(以秒为单位)和文件名,并将它们输出。•管道(|)将这些输出传递到sort命令。•sort-nr:按数值reverse顺序
- java Illegal overloaded getter method with ambiguous type for propert的解决
zwllxs
javajdk
好久不来iteye,今天又来看看,哈哈,今天碰到在编码时,反射中会抛出
Illegal overloaded getter method with ambiguous type for propert这么个东东,从字面意思看,是反射在获取getter时迷惑了,然后回想起java在boolean值在生成getter时,分别有is和getter,也许我们的反射对象中就有is开头的方法迷惑了jdk,
- IT人应当知道的10个行业小内幕
beijingjava
工作互联网
10. 虽然IT业的薪酬比其他很多行业要好,但有公司因此视你为其“佣人”。
尽管IT人士的薪水没有互联网泡沫之前要好,但和其他行业人士比较,IT人的薪资还算好点。在接下的几十年中,科技在商业和社会发展中所占分量会一直增加,所以我们完全有理由相信,IT专业人才的需求量也不会减少。
然而,正因为IT人士的薪水普遍较高,所以有些公司认为给了你这么多钱,就把你看成是公司的“佣人”,拥有你的支配
- java 实现自定义链表
CrazyMizzz
java数据结构
1.链表结构
链表是链式的结构
2.链表的组成
链表是由头节点,中间节点和尾节点组成
节点是由两个部分组成:
1.数据域
2.引用域
3.链表的实现
&nbs
- web项目发布到服务器后图片过一会儿消失
麦田的设计者
struts2上传图片永久保存
作为一名学习了android和j2ee的程序员,我们必须要意识到,客服端和服务器端的交互是很有必要的,比如你用eclipse写了一个web工程,并且发布到了服务器(tomcat)上,这时你在webapps目录下看到了你发布的web工程,你可以打开电脑的浏览器输入http://localhost:8080/工程/路径访问里面的资源。但是,有时你会突然的发现之前用struts2上传的图片
- CodeIgniter框架Cart类 name 不能设置中文的解决方法
IT独行者
CodeIgniterCart框架
今天试用了一下CodeIgniter的Cart类时遇到了个小问题,发现当name的值为中文时,就写入不了session。在这里特别提醒一下。 在CI手册里也有说明,如下:
$data = array(
'id' => 'sku_123ABC',
'qty' => 1,
'
- linux回收站
_wy_
linux回收站
今天一不小心在ubuntu下把一个文件移动到了回收站,我并不想删,手误了。我急忙到Nautilus下的回收站中准备恢复它,但是里面居然什么都没有。 后来我发现这是由于我删文件的地方不在HOME所在的分区,而是在另一个独立的Linux分区下,这是我专门用于开发的分区。而我删除的东东在分区根目录下的.Trash-1000/file目录下,相关的删除信息(删除时间和文件所在
- jquery回到页面顶端
知了ing
htmljquerycss
html代码:
<h1 id="anchor">页面标题</h1>
<div id="container">页面内容</div>
<p><a href="#anchor" class="topLink">回到顶端</a><
- B树、B-树、B+树、B*树
矮蛋蛋
B树
原文地址:
http://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html
B树
即二叉搜索树:
1.所有非叶子结点至多拥有两个儿子(Left和Right);
&nb
- 数据库连接池
alafqq
数据库连接池
http://www.cnblogs.com/xdp-gacl/p/4002804.html
@Anthor:孤傲苍狼
数据库连接池
用MySQLv5版本的数据库驱动没有问题,使用MySQLv6和Oracle的数据库驱动时候报如下错误:
java.lang.ClassCastException: $Proxy0 cannot be cast to java.sql.Connec
- java泛型
百合不是茶
java泛型
泛型
在Java SE 1.5之前,没有泛型的情况的下,通过对类型Object的引用来实现参数的“任意化”,任意化的缺点就是要实行强制转换,这种强制转换可能会带来不安全的隐患
泛型的特点:消除强制转换 确保类型安全 向后兼容
简单泛型的定义:
泛型:就是在类中将其模糊化,在创建对象的时候再具体定义
class fan
- javascript闭包[两个小测试例子]
bijian1013
JavaScriptJavaScript
一.程序一
<script>
var name = "The Window";
var Object_a = {
name : "My Object",
getNameFunc : function(){
var that = this;
return function(){
- 探索JUnit4扩展:假设机制(Assumption)
bijian1013
javaAssumptionJUnit单元测试
一.假设机制(Assumption)概述 理想情况下,写测试用例的开发人员可以明确的知道所有导致他们所写的测试用例不通过的地方,但是有的时候,这些导致测试用例不通过的地方并不是很容易的被发现,可能隐藏得很深,从而导致开发人员在写测试用例时很难预测到这些因素,而且往往这些因素并不是开发人员当初设计测试用例时真正目的,
- 【Gson四】范型POJO的反序列化
bit1129
POJO
在下面这个例子中,POJO(Data类)是一个范型类,在Tests中,指定范型类为PieceData,POJO初始化完成后,通过
String str = new Gson().toJson(data);
得到范型化的POJO序列化得到的JSON串,然后将这个JSON串反序列化为POJO
import com.google.gson.Gson;
import java.
- 【Spark八十五】Spark Streaming分析结果落地到MySQL
bit1129
Stream
几点总结:
1. DStream.foreachRDD是一个Output Operation,类似于RDD的action,会触发Job的提交。DStream.foreachRDD是数据落地很常用的方法
2. 获取MySQL Connection的操作应该放在foreachRDD的参数(是一个RDD[T]=>Unit的函数类型),这样,当foreachRDD方法在每个Worker上执行时,
- NGINX + LUA实现复杂的控制
ronin47
nginx lua
安装lua_nginx_module 模块
lua_nginx_module 可以一步步的安装,也可以直接用淘宝的OpenResty
Centos和debian的安装就简单了。。
这里说下freebsd的安装:
fetch http://www.lua.org/ftp/lua-5.1.4.tar.gz
tar zxvf lua-5.1.4.tar.gz
cd lua-5.1.4
ma
- java-递归判断数组是否升序
bylijinnan
java
public class IsAccendListRecursive {
/*递归判断数组是否升序
* if a Integer array is ascending,return true
* use recursion
*/
public static void main(String[] args){
IsAccendListRecursiv
- Netty源码学习-DefaultChannelPipeline2
bylijinnan
javanetty
Netty3的API
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/ChannelPipeline.html
里面提到ChannelPipeline的一个“pitfall”:
如果ChannelPipeline只有一个handler(假设为handlerA)且希望用另一handler(假设为handlerB)
来
- Java工具之JPS
chinrui
java
JPS使用
熟悉Linux的朋友们都知道,Linux下有一个常用的命令叫做ps(Process Status),是用来查看Linux环境下进程信息的。同样的,在Java Virtual Machine里面也提供了类似的工具供广大Java开发人员使用,它就是jps(Java Process Status),它可以用来
- window.print分页打印
ctrain
window
function init() {
var tt = document.getElementById("tt");
var childNodes = tt.childNodes[0].childNodes;
var level = 0;
for (var i = 0; i < childNodes.length; i++) {
- 安装hadoop时 执行jps命令Error occurred during initialization of VM
daizj
jdkhadoopjps
在安装hadoop时,执行JPS出现下面错误
[slave16]
[email protected]:/tmp/hsperfdata_hdfs# jps
Error occurred during initialization of VM
java.lang.Error: Properties init: Could not determine current working
- PHP开发大型项目的一点经验
dcj3sjt126com
PHP重构
一、变量 最好是把所有的变量存储在一个数组中,这样在程序的开发中可以带来很多的方便,特别是当程序很大的时候。变量的命名就当适合自己的习惯,不管是用拼音还是英语,至少应当有一定的意义,以便适合记忆。变量的命名尽量规范化,不要与PHP中的关键字相冲突。 二、函数 PHP自带了很多函数,这给我们程序的编写带来了很多的方便。当然,在大型程序中我们往往自己要定义许多个函数,几十
- android笔记之--向网络发送GET/POST请求参数
dcj3sjt126com
android
使用GET方法发送请求
private static boolean sendGETRequest (String path,
Map<String, String> params) throws Exception{
//发送地http://192.168.100.91:8080/videoServi
- linux复习笔记 之bash shell (3) 通配符
eksliang
linux 通配符linux通配符
转载请出自出处:
http://eksliang.iteye.com/blog/2104387
在bash的操作环境中有一个非常有用的功能,那就是通配符。
下面列出一些常用的通配符,如下表所示 符号 意义 * 万用字符,代表0个到无穷个任意字符 ? 万用字符,代表一定有一个任意字符 [] 代表一定有一个在中括号内的字符。例如:[abcd]代表一定有一个字符,可能是a、b、c
- Android关于短信加密
gqdy365
android
关于Android短信加密功能,我初步了解的如下(只在Android应用层试验):
1、因为Android有短信收发接口,可以调用接口完成短信收发;
发送过程:APP(基于短信应用修改)接受用户输入号码、内容——>APP对短信内容加密——>调用短信发送方法Sm
- asp.net在网站根目录下创建文件夹
hvt
.netC#hovertreeasp.netWeb Forms
假设要在asp.net网站的根目录下建立文件夹hovertree,C#代码如下:
string m_keleyiFolderName = Server.MapPath("/hovertree");
if (Directory.Exists(m_keleyiFolderName))
{
//文件夹已经存在
return;
}
else
{
try
{
D
- 一个合格的程序员应该读过哪些书
justjavac
程序员书籍
编者按:2008年8月4日,StackOverflow 网友 Bert F 发帖提问:哪本最具影响力的书,是每个程序员都应该读的?
“如果能时光倒流,回到过去,作为一个开发人员,你可以告诉自己在职业生涯初期应该读一本, 你会选择哪本书呢?我希望这个书单列表内容丰富,可以涵盖很多东西。”
很多程序员响应,他们在推荐时也写下自己的评语。 以前就有国内网友介绍这个程序员书单,不过都是推荐数
- 单实例实践
跑龙套_az
单例
1、内部类
public class Singleton {
private static class SingletonHolder {
public static Singleton singleton = new Singleton();
}
public Singleton getRes
- PO VO BEAN 理解
q137681467
VODTOpo
PO:
全称是 persistant object持久对象 最形象的理解就是一个PO就是数据库中的一条记录。 好处是可以把一条记录作为一个对象处理,可以方便的转为其它对象。
BO:
全称是 business object:业务对象 主要作用是把业务逻辑封装为一个对象。这个对
- 战胜惰性,暗自努力
金笛子
努力
偶然看到一句很贴近生活的话:“别人都在你看不到的地方暗自努力,在你看得到的地方,他们也和你一样显得吊儿郎当,和你一样会抱怨,而只有你自己相信这些都是真的,最后也只有你一人继续不思进取。”很多句子总在不经意中就会戳中一部分人的软肋,我想我们每个人的周围总是有那么些表现得“吊儿郎当”的存在,是否你就真的相信他们如此不思进取,而开始放松了对自己的要求随波逐流呢?
我有个朋友是搞技术的,平时嘻嘻哈哈,以
- NDK/JNI二维数组多维数组传递
wenzongliang
二维数组jniNDK
多维数组和对象数组一样处理,例如二维数组里的每个元素还是一个数组 用jArray表示,直到数组变为一维的,且里面元素为基本类型,去获得一维数组指针。给大家提供个例子。已经测试通过。
Java_cn_wzl_FiveChessView_checkWin( JNIEnv* env,jobject thiz,jobjectArray qizidata)
{
jint i,j;
int s
= (min.) # nodes in height-h AVL tree