Fermat Point in Quadrangle POJ 3990 四边形的费马点 数学
题目:https://vjudge.net/problem/POJ-3990
题意:输入四边形四个顶点的坐标(浮点数, 0<=x, y <=1000),求一个点到这四个顶点的距离和最小,输出这个最小的距离和。
关于数据:这题数据可以极其之坑,我现在AC的代码能A掉POJ3990和UVALive5102却A不掉HDU3694,看样还有坑没补上。
说是四边形,实际样例就给了一种四个点都重合的情况,那么还有两两重合,三个重合一个不重合,四点共线。。。。。。至于两个点重合另两个点不重合的情况这就变成三角形了,连四边形的特殊情况都算不上了,同样的情况还有三点共线另一点不共线。
然后四边形分两类,凹四边形和凸四边形都要考虑。
思路:
题意所描述的点叫做费马点,四边形的费马点分两类 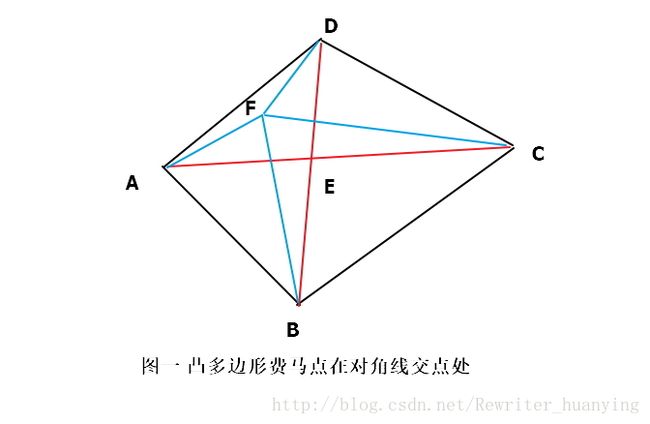
对于凸四边形(任意一条边都使另外两顶点在该边所在直线的同侧),费马点在两对角线交点上,以下作简单证明:
如图一,E点为对角线交点,距离和为BD + AC。任取与E不重合的点F,F到四点的距离为FD +FB +FA +FC,在三角形BDF中,DF+BF > BD , 在三角形AF+CF > AC,因此F点到顶点的距离和大于E点到各顶点的距离和,因此E点即为费马点。
对于凹多边形(存在边使另外两顶点在该边的两侧),费马点在凹顶点处,以下作简单证明。 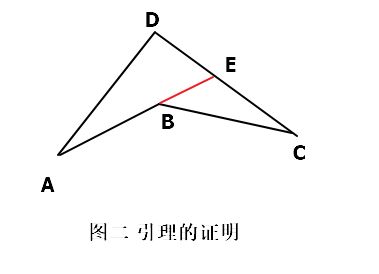
首先证明一个引理,在凸多边形ABCD中,B为凹点,则AD+CD > AB+BC。
延长AB,交CD于E。
AD+CD = AD + DE + CE > AE + CE = AB + BE + CE > AB + BC
(连续使用三角形两边之和大于第三边) 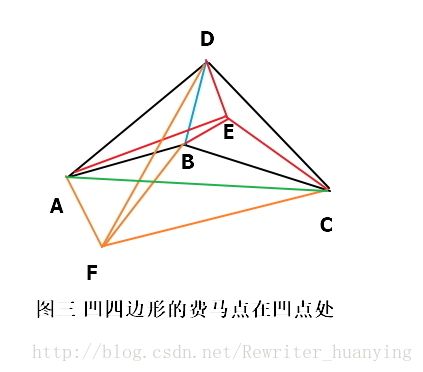
如图二,B点为凹点,距离和为 AB+BC+BD。
考虑以下几种情况:
(1)点在凹四边形内,任取点E,距离和为AE+BE+CE+DE。
由引理可知,AE+CE > AB + BC
在三角形BDE中,BE+DE > BD 因此 AE+BE+CE+DE > AB+BC+BD。
(2)点在凹四边形外,任取点F,距离和为AF+BF+CF+DF。
显然,F在AC线段以外时,F离AC越远,距离和越大,F必定不为费马点;而F若在三角形ABC内时证明方法与(1)中相同。
(3)点在多边形的非凹顶点处,如点A,距离和为AD+AB+AC。
由引理可知AC+AD>BC+BD,因此AB+AC+AD > AB+BC+BD。
其实还有点在边上的情况,也不难证明。
具体实现思路,首先如何判断是凹四边形还是凸四边形,对凸包问题一无所知的我们队想出了一个凹四边形的特点作为区分方法。 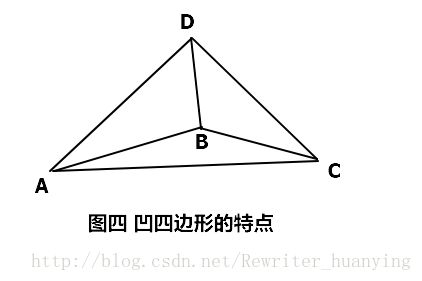
如图四,组成凹四边形的四个顶点可以组成四个三角形,必定能找到一个三角形ADC的面积是其他三个三角形的和,而凹四边形没有这个特点。
那么接下来,如何找到对角线交点?找到两组对角的顶点算出对角线的直线方程联立求解即可解出对角线交点坐标。然而如何找到对角呢?极角排序是个好办法,可惜我当时不会,我用了这样一个特点——在凸四边形中,对角线把另外两顶点分到了对角线两侧,而边则使其他顶点在同侧。两侧和同侧的判断再次借助直线方程,将顶点坐标带入判断点在直线下侧还是上侧。
对于凹四边形,如何找到凹点呢?呃,我直接避开了这个问题,把四个顶点的距离和分别求一遍,最小的肯定是凹点。
另外有个解析几何上的坑,如果用点斜式表示直线需要时时刻刻注意斜率不存在的情况,解两直线交点时解出x需要回代解y的时候注意回代哪一条直线,因为其中一条有可能使分母为零,此时需要换另一条。
啊,这题真是做的想吐,一个数学题愣是写了两百多行代码,还因为手误一直Runtime Error死活查不出错,最后靠使劲出数据把程序测崩了才找出Bug Orz
代码:c++
这代码实在是又臭又长,由于前期想得很不周全在不断修改增补的过程中代码结构变得相当糟糕,仅作参考
#include int , int> > pointpair;
bool input()
{
status = 0;
pointpair.clear();
bool ok = true;
for (int i = 0; i < 4; i++)
{
scanf("%lf%lf", &p[i].x, &p[i].y);
if (p[i].x == -1)
{
ok = false;
}
}
if (!ok)
return ok;
if (p[0] == p[1] && p[0] == p[2] && p[0] == p[3])
{
status = 1;
return ok;
}
int cnt = 0;
for (int i = 0; i < 4; i++)
{
for (int j = i + 1; j < 4; j++)
{
if (p[i] == p[j])
{
status = 2;
cnt++;
}
}
}
if (status == 2)
{
return ok;
}
for (int i = 0; i < 4; i++)
{
double sum = 0;
for (int j = 0; j < 4; j++)
{
if (i != j)
{
sum += area(j);
}
}
if (area(i) == sum)
{
status = 3;
}
}
return ok;
}
void dividepoint()
{
if (status == 1)
{
return;
}
else if (status == 2)
{
for (int i = 1; i < 4; i++)
{
if (!(p[0] == p[i]))
{
vector<int> t;
for (int j = 1; j < 4; j++)
{
if (j != i)
{
t.push_back(j);
}
}
pointpair.push_back(make_pair(0, i));
pointpair.push_back(make_pair(t[0], t[1]));
return;
}
}
}
for (int i = 1; i < 4; i++)
{
if (p[0].x - p[i].x == 0)
{
double dx[10];
int cnt = 0;
for (int j = 1; j < 4; j++)
{
if (j != i)
{
dx[cnt++] = p[0].x - p[j].x;
}
}
if (dx[0] * dx[1] < 0)
{
pointpair.push_back(make_pair(0, i));
vector<int> t;
for (int j = 1; j < 4; j++)
{
if (j != i)
{
t.push_back(j);
}
}
pointpair.push_back(make_pair(t[0], t[1]));
return;
}
}
else
{
double k = (p[0].y - p[i].y) / (p[0].x - p[i].x);
double b = p[0].y - k*p[0].x;
double dy[10];
int cnt = 0;
for (int j = 1; j < 4; j++)
{
if (j != i)
{
dy[cnt++] = k*p[j].x + b - p[j].y;
}
}
if (dy[0] * dy[1] < 0)
{
pointpair.push_back(make_pair(0, i));
vector<int> t;
for (int j = 1; j < 4; j++)
{
if (i != j)
{
t.push_back(j);
}
}
pointpair.push_back(make_pair(t[0], t[1]));
return;
}
}
}
}
double solve()
{
if (status == 1)
{
return 0;
}
else if (status == 2)
{
return getanswer(p[0]);
}
double ans = INF;
if (status == 0)
{
double x0 = p[pointpair[0].first].x;
double y0 = p[pointpair[0].first].y;
double x1 = p[pointpair[0].second].x;
double y1 = p[pointpair[0].second].y;
double xx0 = p[pointpair[1].first].x;
double yy0 = p[pointpair[1].first].y;
double xx1 = p[pointpair[1].second].x;
double yy1 = p[pointpair[1].second].y;
double x = ((y0 - y1)*(xx0 - xx1)*x0 - (yy0 - yy1)*(x0 - x1)*xx0 + (yy0 - y0)*(x0 - x1)*(xx0 - xx1)) / ((y0 - y1)*(xx0 - xx1) - (x0 - x1)*(yy0 - yy1));
double y = x0 == x1 ? ((x - xx0)*(yy0 - yy1)) / (xx0 - xx1) + yy0 : ((x - x0)*(y0 - y1)) / (x0 - x1) + y0;
ans = getanswer(Point(x, y));
}
for (int i = 0; i < 4; i++)
{
ans = min(ans, getanswer(p[i]));
}
return ans;
}
double getanswer(Point t)
{
double ans = 0;
for (int i = 0; i < 4; i++)
{
ans += sqrt((p[i].x - t.x)*(p[i].x - t.x) + (p[i].y - t.y)*(p[i].y - t.y));
}
return ans;
};
double area(int u)
{
int cnt = 0;
int arr[10];
for (int i = 0; i < 4; i++)
{
if (i != u)
{
arr[cnt++] = i;
}
}
cnt = 0;
double a, b, c;
for (int i = 0; i < 3; i++)
{
for (int j = i + 1; j < 3; j++)
{
if (cnt == 0)
a = dist(i, j);
else if (cnt == 1)
b = dist(i, j);
else if (cnt == 2)
c = dist(i, j);
cnt++;
}
}
double p = 1.0 / 2 * (a + b + c);
return sqrt(p*(p - a)*(p - b)*(p - c));
}
double dist(int a, int b)
{
return sqrt((p[a].x - p[b].x)*(p[a].x - p[b].x) + (p[a].y - p[b].y)*(p[a].y - p[b].y));
}
};
int main()
{
quadrangle data;
while (data.input())
{
data.dividepoint();
printf("%.4f\n", data.solve());
}
return 0;
}