详解Python算法之冒泡排序
点击上方"brucepk",选择"置顶公众号"
第一时间关注 Python 技术干货!
阅读文本大概需要 3 分钟。
Python 中常见的排序算法有:冒泡排序、快速排序、插入排序、选择排序、归并排序、堆排序、二叉树排序。
今天给大家分析下冒泡排序,什么是冒泡排序呢?以下是百度百科的解释:冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名冒泡排序。
冒泡排序原理
1、比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2、对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
3、针对所有的元素重复以上的步骤,除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
冒泡排序基础版
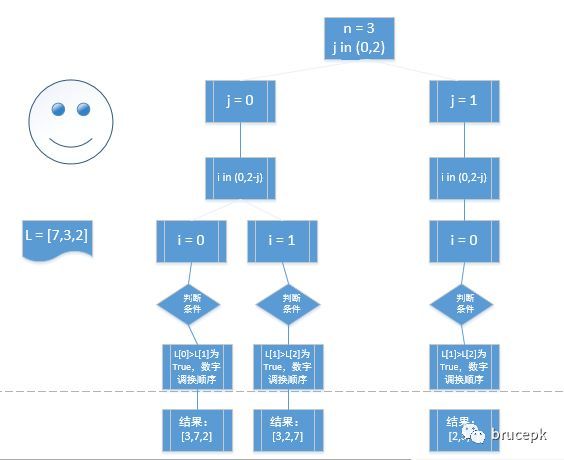
比如我现在要对下面数组进行从小到大排序,为了方便理解,我只放了 3 个元素。
L = [7, 3, 2]
我们想到的用常规方法就是用双层 for 循环去实现。(左右滑动查看全部代码)
def bubble_sort(L):
n = len(L) # n = 3
for j in range(0, n - 1): # (0,2)
for i in range(0, n - 1 - j): # (0,2-j)
if L[i] > L[i + 1]:
L[i], L[i + 1] = L[i + 1], L[i] # 交换位置
bubble_sort(L)
print(L)
# 执行结果
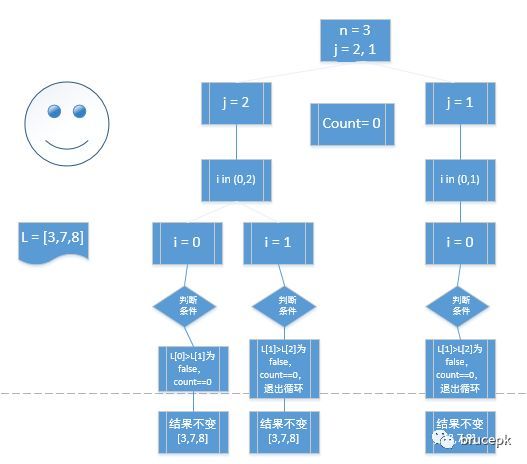
[2, 3, 7]内层循环 i 不断的循环比较左右两个元素的大小,顺序不对则把他们交换顺序,外层循环 j 控制排序的总次数,直到 j 到 n-1 时结束循环。为了便于大家理解,我自己手动画了一张循环流程图。
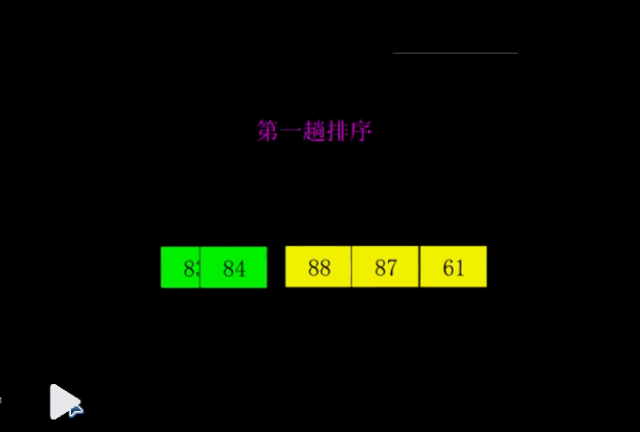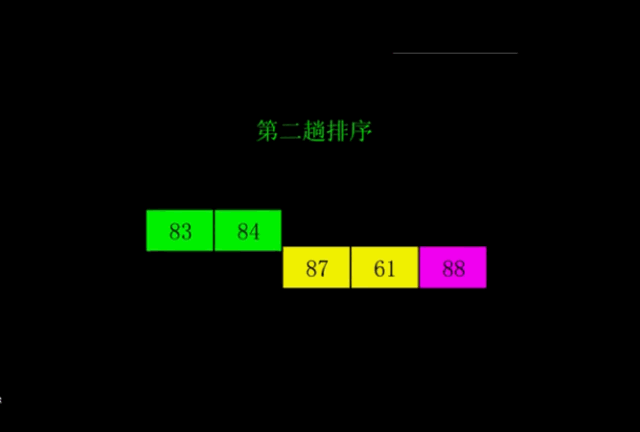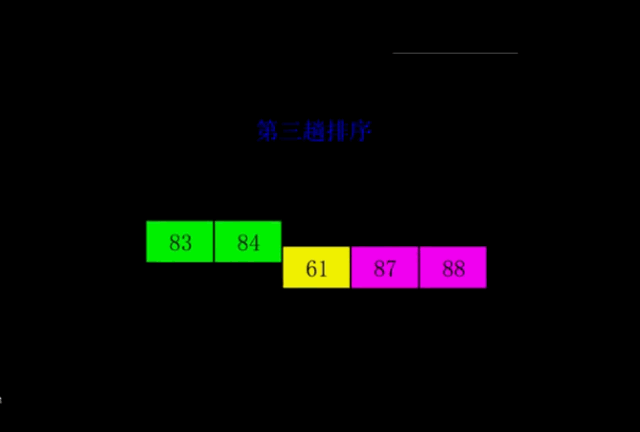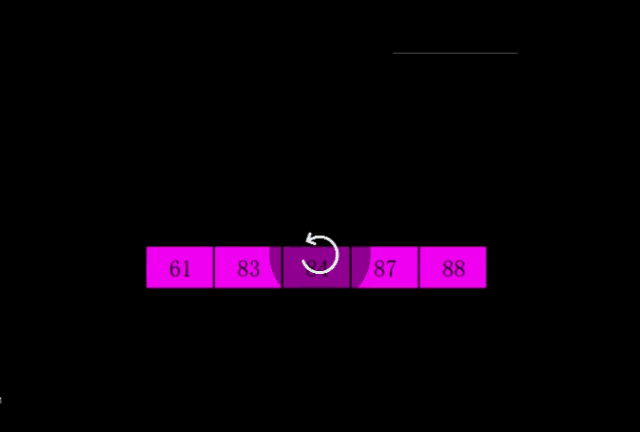
我从网上找了一张冒泡排序过程的动态图,这样就看得更形象了。
冒泡排序优化版
这个双层 for 循环可以把无序的元素进行排序,但是对于已经是有序的元素,我们如果还是用此方法,特别是数据量比较大的情况下,每次都要循环比较一遍,这样对性能没有帮助。作为较真的程序员,我们有没有另一种方法,可以提高下性能呢?答案当然是有的。先看代码。(左右滑动查看全部代码)
def bubble_sort2(L):
for j in range(len(L)-1, 0, -1): # j =2,1
count = 0
for i in range(0, j):
if L[i] > L[i + 1]:
L[i], L[i + 1] = L[i + 1], L[i]
count += 1
if count == 0:
return
L = [3, 7, 8]
bubble_sort2(L)
print(L)
# 执行结果
[3, 7, 8]为了便于理解,我同样只用了 3 个元素,而且是已经从小到大排好顺序的元素。我们在循环中定义了一个变量 count,如果第一次循环后count没有变化,就说明输入的是有序序列,这时我们直接 return 退出循环。上面代码在样式上我还做了点小优化,把外层循环 j 倒着排列,这样 i 直接在 (0,j) 中循环即可。
为了方便大家理解,我也手动画了个流程图。
以上的讲解希望能帮助大家更好的理解冒泡排序。
觉得不错,点赞、赞赏、转发朋友圈都是一种支持。
pk哥还没开通留言功能,不过可以通过点击文末左下角「阅读原文」来留言喔。
推荐阅读:
Python爬虫之b站的正确打开方式
Python骚操作 | 还原已撤回的微信消息
大量 IT 资源免费送,包括但不限于 Python、Java、人工智能、PMP,等等,在公众号内回复「1024」可免费获取。
本公众号的全部文章以整理成目录,后台回复「目录」可查看所有文章。
以梦为马,不负韶华
![]()