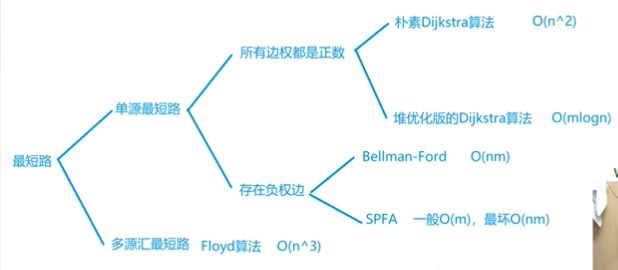
最短路问题总结

最短路问题分类

1）单源最短路
2）多源最短路（不止一个起点）

稠密图： 朴素版Dijstra O(n^2) 数据结构：邻接矩阵
稀疏图： 堆优化版Dijstra O(mlogn) 存储结构：邻接表

考察点：
1）建图 ：将题目抽象成最短路问题

2）Dijstra：基于贪心

朴素版Dijstra：
算法步骤：
1）初始化距离 ：memset(dist,0x3f,sizeof dist)
dist[1]=0;

集合s :存放当前已经确定最短距离的点
2) for i: n
t<-找到不在s中的距离最近的点
s<-
用t 来更新其他所有点的距离
for(从t出去的所有点)
判断是否 dist(x) >dist[t]+w
更新

重边和自环的处理：
1）最短路不会用到重边
2）自环只需要取最短的那条

int Dijstra()
{
    memset(dist,0x3f,sizeof dist);
    
    dist[1]=0;
    for(int i=0;i<n;i++)
    {
        int t=-1;
        //每次迭代的过程中我们都先找到当前未确定的最短距离的点中距离最短的点
        for(int j=1;j<=n;j++)
            if(!st[j] && (t==-1 || dist[t]>dist[j]))
             t=j;
        //更新最短距离的点到其他点的距离
        for(int j=1;j<=n;j++)
            dist[j]=min(dist[j],dist[t]+g[t][j]);
        st[t]=true;
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    
    return dist[n];
}

堆优化的Dijstra：稀疏图

在堆中修改一个数：logn

堆：1）优先队列
2）手写堆

#include

typedef pair PII ;//存距离 存第几个点

priority_queue heap; //小根堆

int dijstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1}); //第一维是距离，第二维是节点
    while(heap.size())
    {
        //获取最短节点
        auto t=heap.top();
        heap.pop();
        int ver=t.second,distance=t.first;
        if(st[ver]) continue; //去备份除垄余节点
        
        st[ver]=true;
        //更新其他节点
        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>distance+w[i])
                dist[j]=distance+w[i];
                
            heap.push({dist[j],j});
        }   
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

Bellman-Ford算法

步骤：
for n 次 //迭代了k次，从1号点经过不超过k条边的最短路的距离
//+备份 ,保证每次遍历一条边都用上次的结果，防止串联
for 所有边a,b,w a—>b (w)
dist[b]=min(dist[b],dist[a]+w)
图示：

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i ++ ) //每次一条边
    {
        memcpy(last, dist, sizeof dist); //备份
        for (int j = 0; j < m; j ++ )
        {
            int  a = edges[j].a,b=edges[j].b,c=edges[j].c;
            dist[b] = min(dist[b], last[a] + c);
        }
    }
}

循环完成后对于每个点都满足： dist[b]<=dist[a]+w;

如果有负权回路—> 最短路径是不一定存在的。
Bellman-Ford算法可以求是否有负权变的。 如果遍历到第n次，还有更新—>说明遍历了n条边（存在负权）。

SPFV算法：要求不能有负环（限制最少的一个算法）

是对Bellman算法的优化：只有当dist[a]变化时，才更新它的所有出边

int spfa()
{
    memset(dist,0x3f,sizeof dist);
    //初始化，将1号点放入队列
    queue<int> q; 
    dist[1]=0;
    q.push(1);
    st[1]=true;   //1号点放入队列
    while(q.size())
    {
        int t=q.front();
        q.pop();
        st[t]=false;
        //更新t的出边节点
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                if(!st[j])   //改动的节点入队，前提是不在队列中
                {
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}

SPFA判断负环：
dist[x] :1~x的最短距离
cnt[x] :边数

//更新操作
dist[x]=dist[t]+w;
cnt[x]=cnt[t]+1;

if(cnt[x]>=n)
存在负环：

注意：1号点可能到不了负环
所有开始需要将所有点都放到队列里面。

bool spfa()
{
    queue<int> q;
    //开始时将所有点都放入队列，因为1号点可能到不了负环
    for(int i=1;i<=n;i++)
    {
        st[i]=true;
        q.push(i);
    }
    while(q.size())
    {
        int t=q.front();
        q.pop();
        st[t]=false;
        
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                cnt[j]=cnt[t]+1;
    
                if(cnt[j]>=n) return true;
                if(!st[j])
                {
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    
    return false;
}

Floyd算法：（多源最短路） ：基于动态规划

存储：d[i,j] :边的长度

void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}