引言
排序是算法恒久不变的话题,也是面试的常客,常见的排序方法有冒泡、选择、插入、堆、希尔、归并、计数、基数和快速排序等等。今天我们学习它们各自的思想及实现。
(本文的代码测试数组为{1,3,2,12,11,10,9,8,7,6,5,4,111,123,233,212,113,156})
冒泡排序
最简单粗暴的排序方法,每一次排序就将最大值交换到最后,最大值在下一次遍历不参与遍历交换,具体步骤如下:
Step1:从待排序序列的起始位置开始,从后往前依次比较各个位置和其后一位置的大小并执行Step2。
Step2:如果当前位置的值大于其后一位置的值,就把他俩的值交换(完成一次全序列比较后,序列最前位置的值即此序列最小值,所以其不需要再参与冒泡)。
Step3:将序列的最后位置从待排序序列中移除。若移除后的待排序序列不为空则继续执行Step1,否则冒泡结束。
代码如下:
/**
* 冒泡排序算法:
* 从头开始遍历, 每一次遍历都将最小值往前交换,n-1次循环,每次循环最小值会上浮
*
* @param arr
*/
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = arr.length - 1; j > i; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr, j, j - 1);
}
}
printArray(arr);
}
}
补充:本例子是从后往前两两交换,将最小值放到最前,也可以从前往后两两交换,将最大值放到最后。
public static void bubbleSort(int[] arr) {
int len = arr.length;
for (int i = 0; i < len; i++) {
for (int j = 0; j < len - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
printArray(arr);
}
}
冒泡排序打印结果如下:
1 2 3 4 12 11 10 9 8 7 6 5 111 113 123 233 212 156
1 2 3 4 5 12 11 10 9 8 7 6 111 113 123 156 233 212
1 2 3 4 5 6 12 11 10 9 8 7 111 113 123 156 212 233
1 2 3 4 5 6 7 12 11 10 9 8 111 113 123 156 212 233
1 2 3 4 5 6 7 8 12 11 10 9 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 12 11 10 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 12 11 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
可以看到,当数组已经排序好,仍然在进行遍历,这显然不必要。当一趟交换后,如果没有发生交换,则表示已经排序完成,不用再继续遍历交换了。代码如下:
/**
* 冒泡排序算法优化:
* 当没有发生遍历交换时,表示已经排好序,直接返回
*
* @param arr
*/
public static void bubbleSort3(int[] arr) {
int len = arr.length;
boolean exFlag = true;//发生交换的标记,默认true
for (int i = 0; i < len; i++) {
if(!exFlag){//上一次遍历未发生过交换
break;
}
exFlag = false;//重置flg,检测本次遍历交换
for (int j = 0; j < len - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
exFlag = true;
}
}
printArray(arr);
}
}
优化后的排序结果为:
1 2 3 11 10 9 8 7 6 5 4 12 111 123 212 113 156 233
1 2 3 10 9 8 7 6 5 4 11 12 111 123 113 156 212 233
1 2 3 9 8 7 6 5 4 10 11 12 111 113 123 156 212 233
1 2 3 8 7 6 5 4 9 10 11 12 111 113 123 156 212 233
1 2 3 7 6 5 4 8 9 10 11 12 111 113 123 156 212 233
1 2 3 6 5 4 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 5 4 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
可以看到遍历次数少于数组长度,无效遍历次数仅多一次(因为上一次遍历发生交换后,不能判断是否排序完毕,所以需要再遍历检测一次)。
冒泡排序时间复杂度为O(1+2+3+4+...+n-1) =O(n*n)。
选择排序
我们发现冒泡排序的本质是每一次遍历就将最值找出来,放到最前或者最后,中间的交换过程是可以省略的,只要将最值找出来和当前的最前或者最后位置交换即可,这就是选择排序的思想,它提现了冒泡排序的本质。排序步骤具体如下:
第一次从R[0]~R[n-1]中选取最小值,与R[0]交换,
第二次从R[1]~R[n-1]中选取最小值,与R[1]交换,
….,
第i次从R[i-1]~R[n-1]中选取最小值,与R[i-1]交换,
…..,
第n-1次从R[n-2]~R[n-1]中选取最小值,与R[n-2]交换,
共通过n-1次,得到一个从小到大排列的有序序列。
同样的,也可以找最大值交换,思路是一样的。代码如下:
/**
* 选择排序, 冒泡排序优化,n-1次循环,每次找到最小值,与排头兵交换
*
* @param arr
*/
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[minIndex] > arr[j]) {
minIndex = j;
}
}
if (minIndex != i) {//和排头兵交换
swap(arr, minIndex, i);
}
printArray(arr);
}
}
打印结果如下:
1 3 2 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 4 11 10 9 8 7 6 5 12 111 123 233 212 113 156
1 2 3 4 5 10 9 8 7 6 11 12 111 123 233 212 113 156
1 2 3 4 5 6 9 8 7 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 113 233 212 123 156
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 212 233 156
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 233 212
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
每一次选择未排序数的最小值放在前面,n次遍历后,排序完成。
每一次寻找插入位置
选择排序时间复杂度为O(1+2+3+4+...+n-1) =O(n*n)。
插入排序
类似于斗地主,手上的牌是排好序的,每新进来一张牌,则寻找插入位置,插入位置左边比新牌小,右边比新牌大。插入排序有两种:直接插入排序和二分查找插入排序。
直接插入排序
思路如下:
1.x[1....maxIndex]为已经排好的序列,a[i]表示新进来的牌,遍历已经排好的序列[0...i-1],找到合适的插入位置index;
2.将index右边的(元素大于a[i])的牌整体后移一位
3.index位置为a[i].
代码如下:
/**
* 插入排序,i = x[1....maxIndex],a[i]表示新进来的牌,遍历已经排好的序列[0...i-1],将大于a[i]的整体右移
*
* @param arr
*/
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int toInsertValue = arr[i];//新来的"牌"
int j = i;//从右往左遍历
while (j > 0 && arr[j - 1] > toInsertValue) {
arr[j] = arr[j - 1];//大的牌右移
j--;
}
arr[j] = toInsertValue;//合适位置
printArray(arr);
}
}
插入排序每一次都要做查找和后移操作(O(2n)),时间复杂度为O(n),需要遍历n-1次,所以直接排序时间复杂度为O(n*n)。
二分查找插入排序
针对已经排好序的序列,插入索引可以通过二分法查找得到,而没必要逐一遍历,代码如下:
/**
* 和直接插入不同,插入排序时,二分法查找插入位置
*
* @param a
*/
public static void binaryInsertSort(int[] a) {
for (int i = 0; i < a.length; i++) {
int temp = a[i];//´ý²åÈ뵽ǰÃæÓÐÐòÐòÁеÄÖµ
int left = 0;
int right = i - 1;
int mid = 0;
while (left <= right) {
mid = (left + right) / 2;
if (temp < a[mid]) {//往左边查找
right = mid - 1;
} else {//往右边查找
left = mid + 1;
}
}
for (int j = i - 1; j >= left; j--) {
//left及右边的元素右移
a[j + 1] = a[j];
}
if (left != i) {//填坑
a[left] = temp;
}
}
}
二分法只是对查找索引做了优化,每一次的查找和后移操作时间复杂度为O(lgn+n),即O(n),需要遍历n-1次,所以时间复杂度仍为O(n*n)。
插入排序的打印结果:
1 3 2 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 3 2 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 12 11 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 11 12 10 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 10 11 12 9 8 7 6 5 4 111 123 233 212 113 156
1 2 3 9 10 11 12 8 7 6 5 4 111 123 233 212 113 156
1 2 3 8 9 10 11 12 7 6 5 4 111 123 233 212 113 156
1 2 3 7 8 9 10 11 12 6 5 4 111 123 233 212 113 156
1 2 3 6 7 8 9 10 11 12 5 4 111 123 233 212 113 156
1 2 3 5 6 7 8 9 10 11 12 4 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 233 212 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 123 212 233 113 156
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 212 233 156
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
快速排序
采用分治思想,每一次遍历都取一个基准值(哨兵),将数组分成两部分,左边的小于哨兵,右边的大于哨兵,然后在分别对两部分继续做快速排序,整个过程可以递归进行,知道高位索引和低位索引相遇,递归结束。代码如下:
/**
* 快速排序,分治法:每一次划分,指定哨兵值,从两端向中间遍历,将大于它的元素放在右边,小于它的元素放在左边,然后将哨兵值填入中间位置
*
* @param arr
*/
public static void puickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
/**
* 递归分治法
*
* @param arr
* @param left
* @param right
*/
private static void quickSort(int[] arr, int left, int right) {
if (left >= right) {//递归结束
return;
}
int pivotPos = partition(arr, left, right);
quickSort(arr, left, pivotPos - 1);
quickSort(arr, pivotPos + 1, right);
}
/**
* 分治法
*
* @param arr
* @param left
* @param right
* @return
*/
private static int partition(int[] arr, int left, int right) {
int target = arr[left];//哨兵值
System.out.println("哨兵:" + target);
while (left < right) {
while (left < right && arr[right] >= target) {
right--;
}
arr[left] = arr[right];//挖坑,小值左移
while (left < right && arr[left] <= target) {
left++;
}
arr[right] = arr[left];//挖坑,大值右移
}
arr[left] = target;//填坑
printArray(arr);
return left;
}
时间复杂度分析:由于用到递归,根据递归的时间复杂度分析:
T(n) = 2T(n/2)+f(n),其中f(n)为partition的复杂度,f(n) = n,迭代到T(1),有T(n) = 2^(logn) T(1) + nlogn = n T[1] + nlogn = n + nlogn
所以快速排序的时间复杂度为O(nlogn)。
希尔排序
希尔排序是一种插入排序算法,又称作缩小增量排序。是对直接插入排序算法的改进。其基本思想是:
先取一个小于n的整数作为第一个增量d1,把全部数据分成个组。所有距离为的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2
2.在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快;
3.后来增量d逐渐缩小, 分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按上一次较大增量作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
4.在大量实验的基础上推出当n在某个范围内时,时间复杂度可以达到O(n^1.3)。
希尔排序实现:
/**
* 每一组的插入排序
* @param arr
*/
private static void shellInsert(int[] arr, int d) {
for (int i = d; i < arr.length; i++) {
int toInsertValue = arr[i];//新来的"牌"
int j = i;//从右往左遍历
while (j > 0 && arr[j - d] > toInsertValue) {
arr[j] = arr[j - d];//后移
j = j - d;
}
arr[j] = toInsertValue;//合适位置
}
printArray(arr);
}
/**
* 希尔排序
* @param arr
*/
public static void shellSort(int[] arr) {
int gap = arr.length / 2;
while (gap >= 1) {//增量递减
shellInsert(arr, gap);
gap /= 2;
}
}
归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
实现代码:
/**
* 归并排序,原理:分治思想,划分两个子序列,然后将两个排好的子序列合并.空间复杂度O(n), 时间复杂度O(nlgn)
*
* @param arr
*/
public static void mergeSort(int[] arr) {
mergeSort(arr, 0, arr.length - 1);
}
/**
* 递归分治
*
* @param arr
* @param left
* @param right
*/
private static void mergeSort(int[] arr, int left, int right) {
if (arr == null || left >= right) {//递归结束
return;
}
int mid = (left + right) / 2;//数组一分为二
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
mergeArr(arr, left, mid, right);
}
/**
* 左右都排好序的前提下,合并arr
*
* @param arr
* @param left
* @param mid
* @param right
*/
public static void mergeArr(int[] arr, int left, int mid, int right) {
int[] tmp = new int[right - left + 1];
int i = left;
int j = mid + 1;
int index = 0;
while (i <= mid && j <= right) {//俩数组索引均未越界
if (arr[i] <= arr[j]) {
tmp[index++] = arr[i++];
} else {
tmp[index++] = arr[j++];
}
}
//数组剩余部分
while (i <= mid) {
tmp[index++] = arr[i++];
}
while (j <= right) {
tmp[index++] = arr[j++];
}
//数组copy
for (int p = 0; p < tmp.length; p++) {
arr[left + p] = tmp[p];
}
printArray(arr);
}
和快速排序类似,它采用分治法思想,时间复杂度为O(n*logn).
计数排序
计数排序是基于数组的值到索引的映射关系而来,引入数组tmp[],里面记录了值到索引的关系:tmp[arr[index]] = 1,当数相同时,tmp[arr[index]] 累加;当数组存在负值时,那么索引的映射关系添加偏移即可:为tmp[arr[index]- min] = 1。然后从低到高遍历tmp数组即可完成排序,这种方法适合数组最值差距不大且分布较均匀的情况。
代码实现:
/**
* 计数排序:找到数组最大值max, 创建引入数组tmp[max+1],
* 然后遍历待排序数组arr[i],做tmp[arr[i]]++操作,这样
* tmp每个位置就记录了arr的元素分布,最后从低到高,将元素还原,实现排序
* 空间复杂度O(n),时间复杂度O(n)
*
* @param arr
*/
public static void countSort(int[] arr) {
int max = max(arr);
int[] countArr = new int[max + 1];
Arrays.fill(countArr, 0);
for (int i = 0; i < arr.length; i++) {
countArr[arr[i]]++;//相应的索引值+1
}
printArray(countArr);
int scanIndex = 0;
//还原数组
for (int i = 0; i < countArr.length; i++) {
for (int j = 0; j < countArr[i]; j++) {
arr[scanIndex++] = i;
}
}
printArray(arr);
}
private static int max(int[] arr) {
int max = Integer.MIN_VALUE;
for (int ele : arr) {
if (ele > max)
max = ele;
}
return max;
}
空间复杂度为O(n),时间复杂度为O(n)。
堆排序
堆排序的思想来源于完全二叉树的性质:
1.节点索引为i的左右子节点索引为2i+1、2i+2;
2.非叶子节点的个数为(n-1)/2,n为节点个数。
大根堆(小根堆)是这样的完全二叉树:它的各个根节点总大于(或小于)子节点,所以根节点为最大值或者最小值,又因为二叉树的操作复杂度为O(lgn),所以效率也较高。时间复杂度为O(nlogn)。
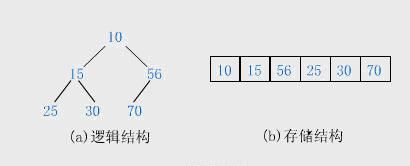
堆的逻辑结构和存储结构如下图:
步骤:
①建堆:
1.对节点[i]大根堆的构造:找到它的叶子节点[2i+1],[2i+2],然后找到这三者的最大值,如果根节点[i]不是最大,则和最大节点交换,由于交换可能会破坏子树的堆结构,因此继续递归构造子树大堆;
2.首先对数组构造最大堆:从下往上遍历二叉树的非叶子节点,每次循环执行步骤1.
②调整堆:每一次构造完大堆,堆顶元素为最大值,将堆顶数组取出,放到最后,缩小键堆范围;
③继续执行步骤①②,直到堆节点个数为1.
代码如下:
/**
* 堆排序
*
* @param arr
*/
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
buildMaxHeap(arr);//先构造最大堆,此时[0]为最大值
for (int i = arr.length - 1; i >= 1; i--) {//i确定了构造最大堆的范围,从len-1开始a
swap(arr, 0, i);//0位置是最大值,放到最后的位置
maxHeap(arr, i, 0);//[0...i]继续构造大堆
}
}
/**
* 整个数组构造最大堆
* @param arr
*/
private static void buildMaxHeap(int[] arr) {
int half = (arr.length - 1) / 2;
for (int i = half; i >= 0; i--) {//从下往上构造最大堆,一直到根节点
maxHeap(arr, arr.length, i);
}
}
/**
* 构建最大堆
*
* @param arr 数组
* @param len 树节点的索引范围
* @param i 根节点索引
*/
private static void maxHeap(int[] arr, int len, int i) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
int tmp = arr[i];
//寻找最大值
if (left < len) {
if (tmp < arr[left]) {
largest = left;
}
}
if (right < len) {
if (arr[largest] < arr[right]) {
largest = right;
}
}
if (i != largest) {//堆发生变化,则将最大值上升到根节点,根节点下沉到叶子节点,
swap(arr, i, largest);//一棵树的最大值放到堆顶
maxHeap(arr, len, largest);// 此时根节点下沉到largest节点,此节点发生变化,子树堆结构可能被破坏,
// 因此子树也需要构造最大堆
}
}
打印结果
212 156 123 113 11 111 9 12 7 6 5 4 10 2 1 8 3 233
156 113 123 12 11 111 9 8 7 6 5 4 10 2 1 3 212 233
123 113 111 12 11 10 9 8 7 6 5 4 3 2 1 156 212 233
113 12 111 8 11 10 9 1 7 6 5 4 3 2 123 156 212 233
111 12 10 8 11 4 9 1 7 6 5 2 3 113 123 156 212 233
12 11 10 8 6 4 9 1 7 3 5 2 111 113 123 156 212 233
11 8 10 7 6 4 9 1 2 3 5 12 111 113 123 156 212 233
10 8 9 7 6 4 5 1 2 3 11 12 111 113 123 156 212 233
9 8 5 7 6 4 3 1 2 10 11 12 111 113 123 156 212 233
8 7 5 2 6 4 3 1 9 10 11 12 111 113 123 156 212 233
7 6 5 2 1 4 3 8 9 10 11 12 111 113 123 156 212 233
6 3 5 2 1 4 7 8 9 10 11 12 111 113 123 156 212 233
5 3 4 2 1 6 7 8 9 10 11 12 111 113 123 156 212 233
4 3 1 2 5 6 7 8 9 10 11 12 111 113 123 156 212 233
3 2 1 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
2 1 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
1 2 3 4 5 6 7 8 9 10 11 12 111 113 123 156 212 233
可见每次构造完大堆,最高节点放到最后。
基数排序
基数排序为计数排序的拓展,需要借助二维数组保存计数排序结果,这里我们称作桶结构,大小为10,按各个位上的数组保存其中,其思想如下:
1.按各个位上的数进行分组计数排序,分配到桶中:
* 第一次排序按个位数的索引放到桶中,收集后,小于等于10的数据完成排序,但大于10的数据仍然乱序;
* 第二次排序按照十位数索引放到桶中,一位数被过滤到buckets[0]中,这样大于10的树按照十位上的数分配到桶中;
* 第三次排序按照百威数索引放到桶中,收集后,一位数和两位数整数被过滤到buckets[0]中,因为1位数已经排好序,本循环完成2位数整数的排序,此时,小于等于100的数均排序好,大于100的三位数整数仍然乱序
* ...
* 每一次遍历就根据同量级的数字作为索引,把元素分配到桶中。
2.收集。每一次遍历结束,就遍历桶,将桶中元素按顺序放入arr,此时buckets[0]中存放的是排序好的数。
3.因为是按各个位上的值进行计数排序,所以遍历的次数又最大值的位数决定;
举例说明:
对于序列:
1,3,2,12,11,10,9,8,7,6,5,4,111,123,233,212,113,156
最大值为三位整数,所以需要遍历三次;
第一次按照个位数分配到桶中:
[10] [1 11 111] [2 12 212] [3 123 233 113] [4] [5] [6 156] [7 8 9]
我们发现个位数在整个数组中一位数整数顺序是正确的,它们在第二次遍历会被放到buckets[0]中,因为它们的十位上为0.桶变成下面的样子:
[1 2 3 4 5 6 7 8 9 10] [11 111] [12 212] [113 123 233] [ ] [ ] [156] 。奇迹出现了,一位整数因为它们的十位为0,所以被过滤到buckets[0]。同样的,第三次遍历会过滤两位整数:
[1 2 3 4 5 6 7 8 9 10 11 12] [111 113 123 156] [212 233].
整个算法的关键是按照各个位上的数分配到桶里去。代码如下:
/**
* 基数排序(计数排序的拓展),桶结构为二维数组,适用于大于0的整数组
* 第一次排序按个位数的索引放到桶中
* 第二次排序按照十位数索引放到桶中
* 第三次排序按照百威数索引放到桶中
* ...
* 每一次遍历就将同量级的数字排序。
* 步骤:
* 1>获取最大数的位数m,它决定了遍历次数
* 2>每一次遍历,取各个元素对应位数x,然后放到桶中
* 3>每一次遍历完成,按顺序搜集数据放到arr中
*
* @param arr
*/
public static void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//找到最大值
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//计算最大值的位数
int count = 0;
int tmp = max;
while (tmp > 0) {
tmp = tmp / 10;
count++;
}
ArrayList> buckets = new ArrayList<>();
//初始化二维数组,大小为10
for (int i = 0; i < 10; i++) {
ArrayList link = new ArrayList<>();
buckets.add(link);
}
for (int i = 0; i < count; i++) {//按位数从低到高遍历
//数据入桶
for (int j = 0; j < arr.length; j++) {
int x = (int) (arr[j] % Math.pow(10, i + 1) / Math.pow(10, i));//个位-十位-百位上的数字提取
ArrayList link = buckets.get(x);
link.add(arr[j]);
}
//遍历桶数据,放到arr里
int index = 0;
for (int m = 0; m < buckets.size(); m++) {
ArrayList link = buckets.get(m);
//取出桶中元素,放到arr里
while (link.size() > 0) {
int item = link.remove(0);
arr[index++] = item;
}
}
printArray(arr);
}
}
好了,由于排序算法方法比较多,这里仅仅分析了常用的算法,篇幅有限,如有纰漏和误人子弟的地方,还望指正!谢谢!
完整代码地址:数据结构与算法学习JAVA描述GayHub地址